
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4 . Конструктивные описания графов
Основные понятия и представления В ходе решения задач на графах к ним применяют различные операции, в общем случае, не похожие на обычные алгебраические. Остановимся на теоретико-множественных операциях, позволяющих описывать построение одних графов из других. Примером использования подобных операций служит рассмотренный ранее процесс построения помеченного дерева по коду Прюфера, в ходе которого ребра склеивались путем отождествления одноименных концевых вершин. Рассмотрим общую постановку задач конструирования графов. Используется конструктор графов, включающий вместе с каждым графом его изоморфные копии. К графам применяется набор операций. Рассматриваются бинарные операции склейки, при выполнении которых производится отождествление изоморфных подграфов При фиксированных графах-операндах
Рисунок 4.1.1
Рисунок 4.1.2
Рисунок 4.1.3. графов Решение задач на графах связано с определением наличия или отсутствия у графов тех или иных свойств. Результирующий граф любой операции склейки сохраняет такие свойства графов-операндов как отсутствие изолированных вершин, петель и ребер. Для сохранения других свойств необходимо введение соответствующих ограничений. Пусть Пусть Á множество графов, обладающих некоторым характеристическим свойством. Граф G называется суперпозицией графов из Á, если G Î Á или G можно получить путем последовательного применения операций Приведем достаточное условие реализуемости графов каноническими суперпозициями. Рассмотрим операции склейки по пустым подграфам (операции H Æ - склейки). Лемма 4.1.1. Если граф G реализуем некоторой H Æ -суперпозицией над Á, то он реализуем и произвольной канонической H Æ -суперпозицией над Á. Доказательство. Любой операции суперпозиции над Á, реализующей граф G, можно поставить в соответствие некоторое покрытие G графами из Á. Так как элементы покрытия, соответствующие H Æ - суперпозиции, пореберно не пересекаются, то любое изменение порядка покрытия, то есть порядка сборки графа, может повлиять лишь на число вершин, включаемых в отождествляемые пустые подграфы тех или иных операций склейки, и не выводит из класса H Æ - суперпозиций. При этом, в частности, можно получить любую каноническую H Æ - суперпозицию над Á. ð
Множество всех графов, полученных из Á с помощью операций Операции с изоморфными подграфами склейки Теорема 4.1.1. Каждый H – замкнутый класс графов имеет единственный элементный базис. Доказательство. Рассмотрим произвольный Замечание. Если система ограничений Из теоремы 4.1.1 получаем Следствие 4.1.1. Каждый замкнутый класс графов имеет единственный элементный базис. Теорема 4.1.2. Существуют замкнутые классы графов со счетными элементными базисами.
Доказательство. Достаточно выделить бесконечную последовательность графов, каждый из которых не может быть получен с помощью суперпозиции из других графов этой последовательности. Замыкание этой последовательности образует искомый класс. Примером такой последовательности может служить последовательность простых циклов Ci, i =1,2,…. Поскольку графы-операнды операций склейки изоморфны подграфам результирующего графа, то в суперпозиции, реализующей простой цикл Cn, не могут использоваться ни циклы Ci, i > n,ни циклы Cj, j < n. ð Логическим следствием теоремы 4.1.1 является Теорема 4.1.3. Мощность множества всех замкнутых классов графов континуальна. Доказательство. Число замкнутых классов множества всех графов Â оценивается сверху числом всех подмножеств графов из Â. Так как Â содержит счетное множество графов, то число подмножеств в Â имеет мощность континуума. Для оценки сверху числа замкнутых классов достаточно заметить, что мощность континуума имеет множество замкнутых классов, элементными базисами которых являются всевозможные подмножества бесконечной последовательности простых циклов Ci, i =1,2,… . ð Так как каждый замкнутый класс является и Следствие 4.1.2. Существуют замкнутые классы графов со счетными элементными базисами. Следствие 4.1.3. Мощность множества всех H – замкнутых классов графов континуальна. Относительно операционных базисов установлено, что каждый замкнутых классов графов имеет хотя бы один операционный базис конечный или счетный [6].
|
||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.34.87 (0.025 с.) |
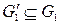 и
и 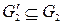 графов-операндов
графов-операндов 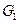 и
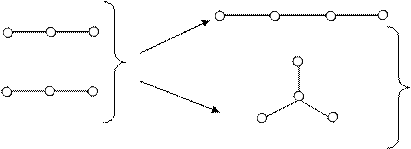
и 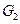 . Операция склейки называется тривиальной, если
. Операция склейки называется тривиальной, если 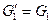 и (или)
и (или) 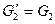 . В общем случае операция склейки не является однозначной. Для результирующих графов G используется обозначение
. В общем случае операция склейки не является однозначной. Для результирующих графов G используется обозначение 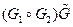 , где
, где 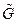 - граф, изоморфный отождествляемым подграфам
- граф, изоморфный отождествляемым подграфам 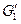 и
и 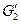 , называемый подграфом склейки.
, называемый подграфом склейки.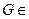



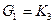
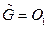
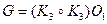


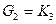
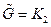
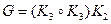



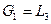



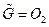
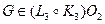
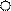
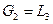
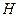 - система ограничений на операции склейки, обеспечивающая сохранение некоторого характеристического свойства графов. В общем случае,
- система ограничений на операции склейки, обеспечивающая сохранение некоторого характеристического свойства графов. В общем случае, 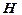 - склейки.
- склейки.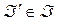 образует полную систему графов
образует полную систему графов 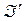 ] H = Á. Минимальная по включению полная система графов
] H = Á. Минимальная по включению полная система графов 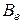 образует элементный базис
образует элементный базис 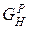 , вершины которого соответствуют графам из P, а дуга
, вершины которого соответствуют графам из P, а дуга 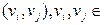
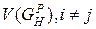 проводится тогда и только тогда, когда граф Gi, соответствующий вершине vi, является графом-операндом хотя бы одной нетривиальной операции
проводится тогда и только тогда, когда граф Gi, соответствующий вершине vi, является графом-операндом хотя бы одной нетривиальной операции  и (или)
и (или) 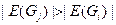 . Из конечности графов Gi и Gj, соответствующих вершинам графа
. Из конечности графов Gi и Gj, соответствующих вершинам графа 


