
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства минимальных нумерацийСодержание книги Поиск на нашем сайте
Пусть G (V, E) граф, содержащий n вершин; A ={ a 1, a 2,..., an }, ai < ai +1, i =1,2,…, n -1 - множество из n натуральных чисел. Взаимнооднозначное отображение j: V (G) ® A называется нумерацией вершин графа G (нумерацией графа), а множество A – нумерующей последовательностью графа G. Рассматривается функционал
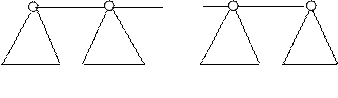
где суммирование производится по всем ребрам графа G. Любая нумерация, на которой достигается Рассмотрим далее класс деревьев. Для задачи построения минимальной нумерации вершин деревьев в качестве исходных поддеревьев удобно взять цепи s (V, E), для которых эта задача решается наиболее просто. Лемма 5.1.1. Нумерация j цепи s (V, E) является минимальной тогда и только тогда, когда j монотонна. Доказательство. Рассмотрим линейную укладку графа s (V, E), разместив вершины цепи s (V, E) вдоль числовой прямой таким образом, чтобы каждая вершина Каждое дерево можно, очевидно, рассматривать как результат объединения пореберно непересекающихся цепей. Для произвольной нумерации j структуру дерева t можно представить следующим образом (рис. 5.1.1). Поддеревья
Рисунок 5.1.1 Лемма 5.1.2. Если j минимальная нумерация дерева t { V, E), то: 1) нумерация цепи s (V 0 , E 0) монотонна, 2) нумерующие последовательности поддеревьев Доказательство. Поскольку множества ребер цепи s (V 0 , E 0) и поддеревьев Предположим, что минимальная нумерация j не удовлетворяет условиям леммы, т.е. нумерация цепи s (V 0 , E 0) не монотонна и (или) найдется хотя бы одно поддерево Вершины Учитывая лемму 5.1.1, для нумераций j и
Из вида оптимизируемого функционала (5.1.1) и способа построения нумерации Из предположения о нумерации j следует, что в (5.1.4) и (или) в (5.1.5) (хотя бы для одного поддерева) имеет место строгое неравенство. Отсюда, сопоставляя (5.1.3) и (5.1.2), получаем
что противоречит условию минимальности нумерации j. ð Следствие 5.1.1. Минимальная нумерацияj дерева t (V, E) является минимальной и на каждом его поддереве
Любой нумерации j графа G, Лемма 5.1.3. Если j минимальная нумерация дерева t (V, E), то вершины Доказательство. Ограничимся рассмотрением вершины Предположим, что вершина Из лемм 5.1.2 и 5.1.3, учитывая равенства (5.1.6), получаем Следствие 5.1.2. Если j минимальная нумерация дерева t (V, E), то его можно разложить на последовательность пореберно непересекающихся цепей s j (Vj, Ej), 1) концевые вершины цепей являются висячими в тех поддеревьях, в которых они выделяются; 2) нумерация каждой цепи монотонна, а нумерующие последовательности всех поддеревьев, образующихся в процессе разложения, сплошные. Все нумерации, в которых можно выделить указанную последовательность цепей, образуют класс нумераций F *. Таким образом, для реализации минимальных нумераций необходимо строить дерево t (V, E) из цепей s j (Vj, Ej),
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.171.192 (0.007 с.) |


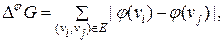 (5.1.1)
(5.1.1)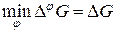 , называется минимальной нумерацией графа G. При решении задачи построения минимальной нумерации достаточно ограничиться рассмотрением связных графов G, поскольку в противном случае задача распадается на несколько независимых подзадач. Из вида минимизируемого функционала (5.1.1) следует, что, не ограничивая общности рассмотрения, можно полагать, что нумерующая последовательность содержит n первых натуральных чисел, т.е. A = { 1,2,..., n }. При этом
, называется минимальной нумерацией графа G. При решении задачи построения минимальной нумерации достаточно ограничиться рассмотрением связных графов G, поскольку в противном случае задача распадается на несколько независимых подзадач. Из вида минимизируемого функционала (5.1.1) следует, что, не ограничивая общности рассмотрения, можно полагать, что нумерующая последовательность содержит n первых натуральных чисел, т.е. A = { 1,2,..., n }. При этом 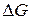 не больше, чем при выборе любой другой нумерующей последовательности.
не больше, чем при выборе любой другой нумерующей последовательности.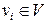 попала в точку с координатой
попала в точку с координатой 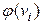 . При этом каждому ребру
. При этом каждому ребру 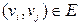 будет соответствовать отрезок [
будет соответствовать отрезок [ 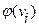 ,
, 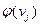 ]. Из вида функционала (5.1.1) следует, что
]. Из вида функционала (5.1.1) следует, что 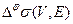 равно сумме длин всех таких отрезков. Поскольку наибольшее и наименьшее значения номеров вершин фиксированы, то указанная сумма будет минимальной тогда и только тогда, когда отрезки [
равно сумме длин всех таких отрезков. Поскольку наибольшее и наименьшее значения номеров вершин фиксированы, то указанная сумма будет минимальной тогда и только тогда, когда отрезки [ 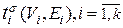 порождены ребрами, не принадлежащими цепи s (V 0 , E 0), соединяющей вершины
порождены ребрами, не принадлежащими цепи s (V 0 , E 0), соединяющей вершины 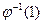 и
и 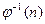 .
.
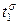
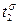 ...
... 
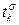
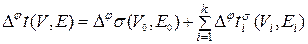 . (5.1.2)
. (5.1.2)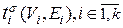 , нумерующая последовательность которого не является сплошной. Построим по j нумерацию
, нумерующая последовательность которого не является сплошной. Построим по j нумерацию 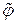 , удовлетворяющую условиям леммы, что всегда возможно при сплошной нумерующей последовательности всего дерева, и обладающую следующими свойствами.
, удовлетворяющую условиям леммы, что всегда возможно при сплошной нумерующей последовательности всего дерева, и обладающую следующими свойствами.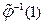 и
и 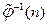 совпадают соответственно с вершинами
совпадают соответственно с вершинами 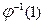 и
и 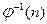 , порядок нумерации внутри каждого поддерева
, порядок нумерации внутри каждого поддерева 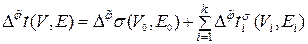 . (5.1.3)
. (5.1.3)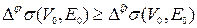 . (5.1.4)
. (5.1.4)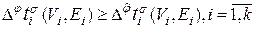 (5.1.5)
(5.1.5)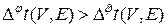 ,
,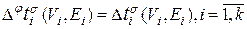 . (5.1.6)
. (5.1.6)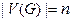 можно сопоставить двойственную нумерацию
можно сопоставить двойственную нумерацию  такую, что
такую, что 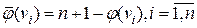 . Очевидно, что
. Очевидно, что 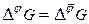 . Вершины графа степени один будем называть для краткости висячими.
. Вершины графа степени один будем называть для краткости висячими.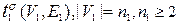 . Из леммы 5.1.2 следует, что его нумерующая последовательность состоит из чисел 1,2,…,
. Из леммы 5.1.2 следует, что его нумерующая последовательность состоит из чисел 1,2,…, 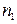 . Построим нумерацию j 1, совпадающую с нумерацией j на всехвершинах
. Построим нумерацию j 1, совпадающую с нумерацией j на всехвершинах 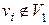 , а на вершинах
, а на вершинах 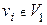 совпадающую с двойственной нумерацией:
совпадающую с двойственной нумерацией: 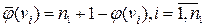 . При переходе к нумерации j 1 монотонность нумерации цепи s (V 0 , E 0), очевидно, сохранится. Поскольку
. При переходе к нумерации j 1 монотонность нумерации цепи s (V 0 , E 0), очевидно, сохранится. Поскольку 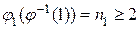 , то
, то 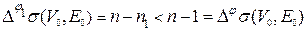 . Так как
. Так как 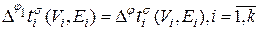 , то, сравнивая разложения (5.1.2) для нумераций j и j 1, получаем
, то, сравнивая разложения (5.1.2) для нумераций j и j 1, получаем 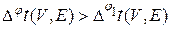 , что противоречит условию минимальности нумерации j. ð
, что противоречит условию минимальности нумерации j. ð таких, что:
таких, что: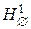 - склейки). Пусть
- склейки). Пусть 


