Поразрядная сортировка для массивов

Одним из известных алгоритмов является метод, называемый «сортировкой подсчетом».

Пусть у нас есть массив source из n десятичных цифр (m = 10).
Например, source[7] = {7, 9, 8, 5, 4, 7, 7}, n=7. Здесь положим const k=1.

1. Создать массив count из m элементов (счетчиков).

2. Присвоить count[i] количество элементов source, равных i. Для этого:

· проинициализовать count[] нулями;

· пройти по source от начала до конца, для каждого числа увеличивая элемент count с соответствующим номером;

· for(i=0; i<n; i++) count [ source[i] ]++;

В нашем примере count[] = { 0, 0, 0, 0, 1, 1, 0, 3, 1, 1 }.

3. Присвоить count[i] значение, равное сумме всех элементов до данного: count[i] = count[0]+count[1]+...count[i-1]. В нашем примере    count[] = { 0, 0, 0, 0, 1, 2, 2, 2, 5, 6 }. Эта сумма является количеством чисел исходного массива, меньших i.

4. Произвести окончательную расстановку.

Для каждого числа source[i] мы знаем, сколько определено чисел меньше него - это значение хранится в count[ source[i] ]. Таким образом, нам известно окончательное место числа в упорядоченном массиве: если есть K чисел меньше данного, то оно должно стоять на позиции K+1.
Осуществляем проход по массиву source слева направо, одновременно заполняя выходной массив dest:

for (i=0; i<n; i++) { c = source[i]; dest[ count[c] ] = c; count[c]++; // для повторяющихся чисел }

Таким образом, число c=source[i] ставится на место count[c]. На этот случай, если числа повторяются в массиве, предусмотрен оператор count[c]++, который увеличивает значение позиции для следующего числа c, если таковое будет.

Циклы занимают (n + m) времени. Столько же требуется памяти.

Итак, мы научились за (n + m) сортировать цифры. А от цифр до строк и чисел - 1 шаг. Пусть у нас в каждом ключе k цифр (m = 10). Аналогично случаю со списками отсортируем их в несколько проходов от младшего разряда к старшему (рис. 23).

Исходная k =3 последовательность	Первый проход по 3-му разряду	Второй проход по 2-му разряду	третий проход по 1-му разряду
523	523	523	088
153	153	235	153
088	554	153	235
554	235	554	523
235	088	088	553
	↑	↑	↑
Offset (номер позиции)	3	2	1

Рис. 23

Общее количество операций составляет k(n+m), при используемой дополнительно памяти (n+m). Эта схема допускает небольшую оптимизацию. Заметим, что сортировка по каждому байту состоит из 2 проходов по всему массиву: на первом шаге и на четвертом. Однако можно создать сразу все массивы count[] (по одному на каждую позицию) за один проход. Неважно, как расположены числа - счетчики не меняются, поэтому это изменение корректно. Таким образом, первый шаг будет выполняться один раз за всю сортировку, а значит, общее количество проходов изменится с 2k на k+1.

 

 

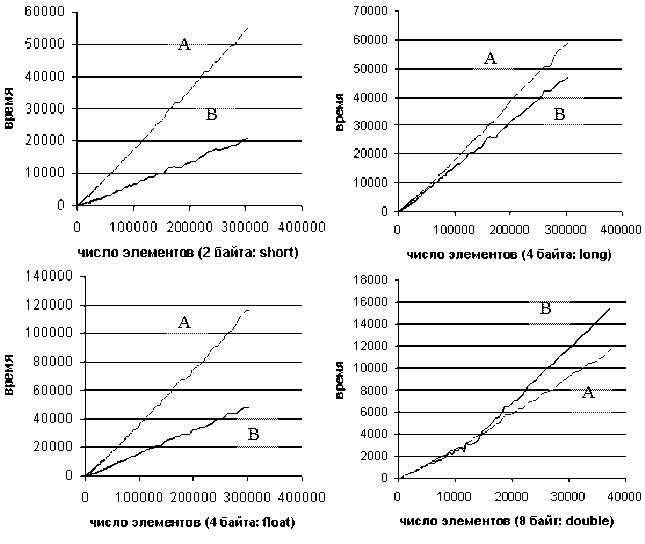
Эффективность поразрядной сортировки

Рост быстрой сортировки мы уже знаем: O(nlogn). Судя по оценке, поразрядная сортировка растет линейным образом по n, так как k, m - константы.

Также она растет линейным образом по k - при увеличении длины типа (количества разрядов) соответственно возрастает число проходов. Однако в последний пункт реальные условия вносят свои коррективы.

Дело в том, что основной цикл сортировки по i -му байту состоит в движении указателя uchar* bp шагами sizeof(T) по массиву для получения очередного разряда. Когда T=char, шаг равен 1, T=short - шаг равен 2, T=long - шаг равен 4. Чем больше размер типа, тем менее последовательный доступ к памяти осуществляется, а это весьма существенно сказывается на скорости работы. Поэтому реальное время возрастает чуть быстрее, нежели теоретическое.

Кроме того, поразрядная сортировка уже по своей сути неинтересна для малых массивов. Каждый проход содержит минимум 256 итераций, поэтому при небольших n общее время выполнения (n+m) определяется константой m=256.

Поведение неестественно, так как проходы выполняются полностью, вне зависимости от исходного состояния массива. Поразрядная сортировка является устойчивой.

Результаты тестирования

На диаграммах (рис. 24) изображены результаты сравнений поразрядной сортировки (линия В) и быстрой (линия А), причем использовалась функция sort() из библиотеки STL.

Рис. 24

Анализ диаграмм:

• short
  Благодаря малой разрядности и простоте внутренних циклов поразрядная перегнала быструю сортировку уже на 100 элементах.
• long
  При переходе к типу long произошло двукратное увеличение количества проходов RadixPass, поэтому худшая асимптотика быстрой сортировки показала себя лишь после 600 элементов, где она начала отставать.
• float
  По графику видно, что для этого типа поразрядная сортировка оказалась гораздо эффективнее, нежели для long. В чем дело, ведь размер одинаков - 4 байта? Оказывается, на типе float резко возрастает время работы быстрой сортировки. Возможно, это связано с тем, что процессор, прежде чем делать какие-либо операции, переводит его в double, а потом работает с этим типом, который в 2 раза больше по размеру. Так или иначе, быстрая сортировка стала работать в 2 раза медленнее, и поразрядная вышла вперед после 100 элементов.
• double
  График показан с десятикратным увеличением. Размер типа увеличился в 2 раза, поэтому для небольших n поразрядная сортировка, конечно, отстает, но перегоняет быструю на массивах из нескольких тысяч элементов. Небольшое преимущество RadixSort длится приблизительно до 16000 элементов, когда данные начинают вылезать за пределы кэша. Соответственно, начинает играть свою роль медленный непоследовательный доступ (с шагами по 8 байт) к основной памяти. В результате поразрядная сортировка снова выбивается вперед лишь после 500000 элементов.

В программах используются переопределения:

typedef double     real;typedef unsigned long ulong;typedef unsigned short ushort;typedef unsigned char uchar;

Под переменной size принимается количество элементов в массиве, а для обозначения индекса последнего элемента используется N. Очевидно, что size=N+1.