Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация методов сортировкиСтр 1 из 6Следующая ⇒
Введение Пожалуй, никакая другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. К сожалению, нельзя сказать, что существует некий "универсальный", наилучший алгоритм. Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом. Для того чтобы обоснованно сделать такой выбор, рассмотрим параметры, по которым будет производиться оценка алгоритмов. 1. Время сортировки: основной параметр, характеризующий быстродействие алгоритма. 2. Память: ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будут учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы. 3. Устойчивость: устойчивая сортировка не меняет взаимного расположения равных элементов. Такое свойство может быть очень полезным, если они состоят из нескольких полей, а сортировка происходит по одному из них.
Исходные данные
Пример работы устойчивой сортировки Рис. 1 На рис. 1 приведен пример устойчивой работы алгоритма. Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" осталось прежним: элемент с полем "a", затем - с "b", затем - с "c".
Пример работы неустойчивой сортировки На рис. 2 приведен пример неустойчивой работы алгоритма. Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось. 4. Естественность поведения: эффективность метода при обработке уже отсортированных или частично отсортированных данных. Алгоритм ведет себя естественно и работает лучше, если учитывает эту характеристику входной последовательности. В общей постановке задача ставится следующим образом. Пусть есть последовательность a0, a1... an и функция сравнения, которая на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.
Возможна ситуация, когда элементы состоят из нескольких полей (рис. 3).
Рис. 3 struct element { field x; field y; };Если значение функции сравнения зависит только от поля x, то x называют ключом, по которому производится сортировка, или ключом сортировки. На практике в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма. Тип данных ключа должен включать операции сравнения ("=", ">", "<", ">=" и "<="). Задачей сортировки является преобразование исходной последовательности в последовательность, содержащую те же записи, но в порядке возрастания (или убывания) значений ключа. Поскольку сортировка основана только на значениях ключа и никак не затрагивает оставшиеся поля записей, можно говорить о сортировке массивов ключей. Сортировка выбором Идея метода состоит в том, чтобы создавать отсортированную последовательность путем присоединения к ней одного элемента за другим в правильном порядке. Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)- м. На i -м шаге выбираем наименьший из элементов a[i]... a[n] и меняем его местами с a[i]. Последовательность шагов при n=5 изображена на рис. 4.
Рис. 4 Вне зависимости от номера текущего шага i последовательность a[0]...a[i] (выделена на рисунке курсивом) является упорядоченной. Таким образом, на (n-1)- м шаге вся последовательность, кроме a[n] оказывается отсортированной, а a[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево. template<class T>void selectSort(T a[], long size) { long i, j, k; T x; for(i=0; i < size; i++) { // i - номер текущего шага k=i; x=a[i]; for(j=i+1; j < size; j++) // цикл выбора наименьшего элемента if (a[j] < x) { k=j; x=a[j]; // k - индекс наименьшего элемента } a[k] = a[i]; a[i] = x; // меняем местами наименьший с a[i] }}Для нахождения наименьшего элемента из n+1 рассматриваемых алгоритм совершает n сравнений. С учетом того, что количество рассматриваемых на очередном шаге элементов уменьшается на единицу, общее количество операций:
n + (n-1) + (n-2) + (n-3) +... + 1 = 1/2 * (n2+n) = О(n2). Таким образом, так как число обменов всегда будет меньше числа сравнений, время сортировки растет квадратично относительно количества элементов. Алгоритм не использует дополнительной памяти: все операции происходят "на месте". Для определения устойчивости метода рассмотрим последовательность из трех элементов, каждый из которых имеет два поля, а сортировка идет по первому из них (рис. 5).
Рис. 5. Результат сортировки такой последовательности можно увидеть уже после шага 0, так как больше обменов не будет. Порядок ключей 2a, 2b был изменен на 2b, 2a, поэтому метод неустойчив. Если входная последовательность почти упорядочена, то сравнений будет столько же, то есть алгоритм ведет себя неестественно. Сортировка вставками Одним из наиболее простых и естественных методов внутренней сортировки является сортировка с простыми включениями или вставками. Идея алгоритма очень проста. Пусть имеется массив ключей a[1], a[2],..., a[n]. Для каждого элемента массива, начиная со второго, производится сравнение с элементами с меньшим индексом (элемент a[i] последовательно сравнивается с элементами a[i-1], a[i-2]...) и до тех пор, пока для очередного элемента a[j] выполняется соотношение a[j] > a[i], a[i] и a[j] меняются местами. Если удается встретить такой элемент a[j], что a[j] <= a[i], или если достигнута нижняя граница массива, производится переход к обработке элемента a[i+1] (пока не будет достигнута верхняя граница массива). Аналогичным образом делаются проходы по части массива, и аналогичным же образом в его начале "вырастает" отсортированная последовательность. Однако в сортировке «пузырьком» или «выбором» можно было четко заявить, что на i -м шаге элементы a[0]...a[i] стоят на правильных местах и никуда более не переместятся. Здесь же подобное утверждение будет более слабым: последовательность a[0]...a[i] упорядочена. При этом по ходу алгоритма в нее будут вставляться все новые элементы. На i -м шаге работы алгоритма последовательность разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n]. На следующем, (i+1)- м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива. Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте (вставка завершена), либо они меняются местами и процесс повторяется (рис. 8).
Последовательность на текущий момент. Часть a[0]… a[2] уже упорядочена.
Вставка числа 2 в отсортированную подпоследовательность. Сравниваемые пары выделены
Рис. 8 Таким образом, в процессе вставки мы "просеиваем" элемент x к началу массива, останавливаясь в случае, когда: 1) найден элемент, меньший x, или 2) достигнуто начало последовательности. Иногда этот метод называют сортировкой «просеиванием». template<class T>void insertSort(T a[], long size) { T x; long i, j; for (i=0; i < size; i++) { // цикл проходов, i - номер прохода x = a[i]; // поиск места элемента в готовой последовательности for (j=i-1; j>=0 && a[j] > x; j--) a[j+1] = a[j]; // сдвигаем элемент направо, пока не дошли // место найдено, вставить элемент a[j+1] = x; }}Аналогично сортировке выбором, среднее, а также худшее число сравнений и пересылок оцениваются О(n2), дополнительная память при этом не используется. Хорошим показателем сортировки является весьма естественное поведение: почти отсортированный массив будет «досортирован» очень быстро. Именно эти качества алгоритма делают его широко применимым на практике в соответствующих ситуациях.
Сортировка Шелла Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками. Рассмотрим следующий алгоритм сортировки массива a[0].. a[15] (рис. 11).
Рис. 11 1. Вначале сортируем простыми вставками каждые 8 групп из двух элементов (a[0], a[8]), (a[1], a[9]),..., (a[7], a[15]) (рис.12).
Рис. 12 2. Потом сортируем каждую из четырех групп по четыре элемента (a[0], a[4], a[8], a[12]),..., (a[3], a[7], a[11], a[15]) (рис. 13).
Рис.13 В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п. 3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]) (рис. 14).
Рис. 14
4. В конце сортируем вставками все 16 элементов (рис. 15).
Рис. 15 Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные? Они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.
Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности. Использованный в примере набор - 8, 4, 2, 1 – является обычным выбором в тех случаях, когда количество элементов представляет собой степень двойки. Однако гораздо лучший вариант предложил Р.Седжвик. Его последовательность имеет вид:
При использовании таких приращений среднее количество операций: O(n7/6), в худшем случае - порядка O(n4/3). Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5,... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке. При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size. int increment(long inc[], long size) { int p1, p2, p3, s; p1 = p2 = p3 = 1; s = -1; do { if (++s % 2) { inc[s] = 8*p1 - 6*p2 + 1; } else { inc[s] = 9*p1 - 9*p3 + 1; p2 *= 2; p3 *= 2; } p1 *= 2; } while(3*inc[s] < size); return s > 0? --s: 0;} template<class T>void shellSort(T a[], long size) { long inc, i, j, seq[40]; int s; // вычисление последовательности приращений s = increment(seq, size); while (s >= 0) { // сортировка вставками с инкрементами inc[] inc = seq[s--]; for (i = inc; i < size; i++) { T temp = a[i]; for (j = i-inc; (j >= 0) && (a[j] > temp); j -= inc) a[j+inc] = a[j]; a[j+inc] = temp; } }}Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s] > size. Пирамидальная сортировка Пирамидальная сортировка является первым из рассматриваемых методов, быстродействие которых оценивается как O(n log n). В качестве вступления к основному методу рассмотрим перевернутую сортировку выбором. Во время прохода, вместо вставки наименьшего элемента в левый конец массива, будем выбирать наибольший элемент, а готовую последовательность строить в правом конце. Пример действий для массива a[0]... a[7]: 44 55 12 42 94 18 06 67 исходный массив 44 55 12 42 67 18 06 | 94 94 <-> 67 44 55 12 42 06 18 | 67 94 67 <-> 06 44 18 12 42 06 | 55 67 94 55 <-> 18 06 18 12 42 | 44 55 67 94 44 <-> 06 06 18 12 | 42 44 55 67 94 42 <-> 42 06 12 | 18 42 44 55 67 94 18 <-> 12 06 | 12 18 42 44 55 67 94 12 <-> 12Вертикальной чертой отмечена левая граница уже отсортированной (правой) части массива.
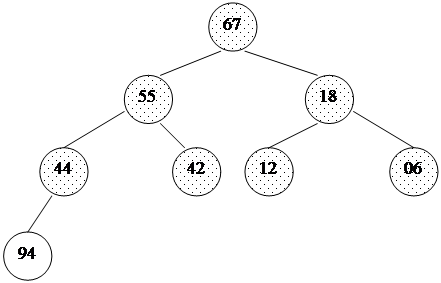
Рассмотрим оценку количества операций подробнее. Всего выполняется n шагов, каждый из которых состоит в выборе наибольшего элемента из последовательности a[0]..a[i] и последующем обмене. Выбор происходит последовательным перебором элементов последовательности, поэтому необходимое на него время: O(n). Итак, n шагов по O(n) каждый - это O(n2). Произведем усовершенствование: построим структуру данных, позволяющую выбирать максимальный элемент последовательности не за O(n), а за O(log n) времени. Тогда общее быстродействие сортировки будет n*O(log n) = O(n log n). Эта структура также должна позволять быстро вставлять новые элементы (чтобы быстро ее построить из исходного массива) и удалять максимальный элемент (он будет помещаться в уже отсортированную часть массива - его правый конец). Итак, назовем пирамидой (Heap) бинарное дерево высоты k, в котором: · все узлы имеют глубину k или k-1, то есть дерево сбалансированное; ·
Рис. 16 · выполняется "свойство пирамиды": каждый элемент меньше, либо равен родителю (рис. 17).
Рис. 17
Как хранить пирамиду? Наименее хлопотно - поместить ее в массив. Соответствие между геометрической структурой пирамиды как дерева и массивом устанавливается по следующей схеме:
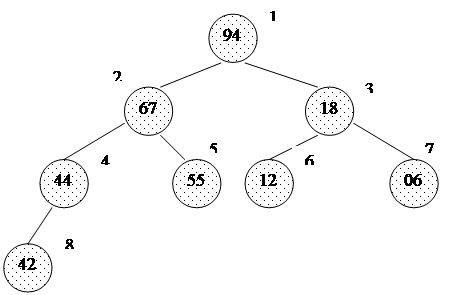
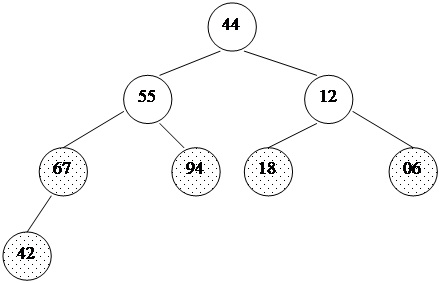
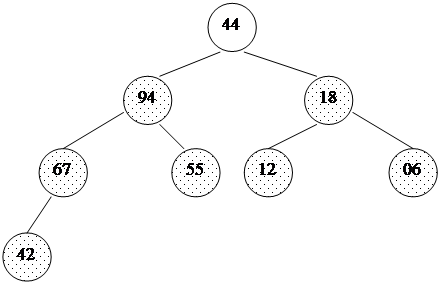
Таким образом, для массива, хранящего в себе пирамиду, выполняется следующее характеристическое свойство: a[i] >= a[2i+1] и a[i] >= a[2i+2]. Плюсы такого хранения пирамиды очевидны: · никаких дополнительных переменных, нужно лишь понимать схему; · узлы хранятся от вершины и далее вниз, уровень за уровнем; · узлы одного уровня хранятся в массиве слева направо. Запишем в виде массива пирамиду, изображенную выше. Слева направо, сверху вниз: 94 67 18 44 55 12 06 42. На рисунке 17 место элемента пирамиды в массиве обозначено цифрой справа вверху от него. Восстановить пирамиду из массива как геометрический объект легко - достаточно вспомнить схему хранения и нарисовать, начиная от корня. Шаг 1: построение пирамиды Начать построение пирамиды можно с a[k]...a[n], k = [size/2]. Эта часть массива удовлетворяет свойству пирамиды, так как не существует индексов i, j: i = 2i+1 (или j = 2i+2), потому что такие i, j находятся за границей массива. Следует заметить, что a[k]...a[n] не является пирамидой как самостоятельный массив. Это, вообще говоря, неверно: его элементы могут быть любыми. Свойство пирамиды сохраняется лишь в рамках исходного, основного массива a[0]...a[n]. Далее будем расширять часть массива, обладающую столь полезным свойством, добавляя по одному элементу за шаг. Следующий элемент на каждом шаге добавления - тот, который стоит перед уже готовой частью. Чтобы при добавлении элемента сохранялась пирамидальность, будем использовать следующую процедуру расширения пирамиды a[i+1]...a[n] на элемент a[i] влево: 1. Смотрим на сыновей слева и справа (в массиве это a[2i+1] и a[2i+2]) и выбираем наибольшего из них. 2. Если этот элемент больше a[i] - меняем его с a[i] местами и идем к шагу 2, имея в виду новое положение a[i] в массиве. Иначе процедура заканчивается. Новый элемент "просеивается" сквозь пирамиду. template<class T>void downHeap(T a[], long k, long n) { // процедура просеивания следующего элемента // До процедуры: a[k+1]...a[n] - пирамида // После: a[k]...a[n] - пирамида T new_elem; long child; new_elem = a[k]; while(k <= n/2) { // пока у a[k] есть дети child = 2*k; // выбираем большего сына if(child < n && a[child] < a[child+1]) child++; if(new_elem >= a[child]) break; // иначе a[k] = a[child]; // переносим сына наверх k = child; } a[k] = new_elem;}Учитывая, что высота пирамиды h <= log n, этот метод сортировки требует O(log n) времени. Полный код процедуры построения пирамиды будет иметь вид: // вызвать downheap O(n) раз для преобразования массива в пирамиду целикомfor(i=size/2; i >= 0; i--) downHeap(a, i, size-1);Ниже дана иллюстрация процесса для пирамиды из 8 элементов: 44 55 12 42 // 94 18 06 67 Справа - часть массива, удовлетворяющая 44 55 12 // 67 94 18 06 42 свойству пирамиды, 44 55 // 18 67 94 12 06 42 остальные элементы добавляются 44 // 94 18 67 55 12 06 42 один за другим, справа налево. // 94 67 18 44 55 12 06 42В геометрической интерпретации ключи из начального отрезка a[size/2]...a[n] являются листьями в бинарном дереве, как изображено ниже. Один за другим остальные элементы продвигаются на свои места, и так пока не будет построена вся пирамида. На рис. 18, 19 изображен процесс построения. Неготовая часть пирамиды (начало массива) окрашена в белый цвет, удовлетворяющий свойству пирамиды конец массива - заштрихован. Шаг 2: сортировка Итак, задача построения пирамиды из массива успешно решена. Как видно из свойств пирамиды, в корне всегда находится максимальный элемент. Отсюда вытекает алгоритм фазы 2: 1. Берем верхний элемент пирамиды a[0]...a[n] (первый в массиве) и меняем с последним местами. Теперь "забываем" об этом элементе и далее рассматриваем массив a[0]...a[n-1]. Для превращения его в пирамиду достаточно просеять лишь новый первый элемент. 2. Повторяем шаг 1, пока обрабатываемая часть массива не уменьшится до одного элемента (рис. 20). Очевидно, в конец массива каждый раз попадает максимальный элемент из текущей пирамиды, поэтому в правой части постепенно возникает упорядоченная последовательность. 94 67 18 44 55 12 06 42 // иллюстрация 2-й фазы сортировки 67 55 44 06 42 18 12 // 94 во внутреннем представлении пирамиды 55 42 44 06 12 18 // 67 94 44 42 18 06 12 // 55 67 94 42 12 18 06 // 44 55 67 94 18 12 06 // 42 44 55 67 94 12 06 // 18 42 44 55 67 94 06 // 12 18 42 44 55 67 94
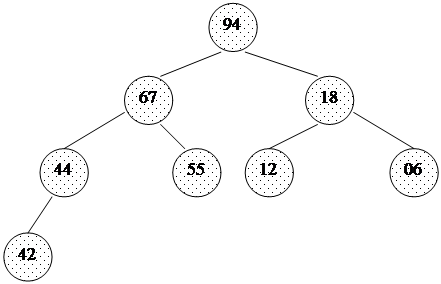
Исходная картина, 94, 18, 06, 67 - листья Сравнили 42 и 67 и поменяли их местами
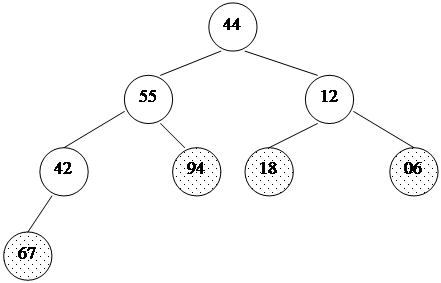
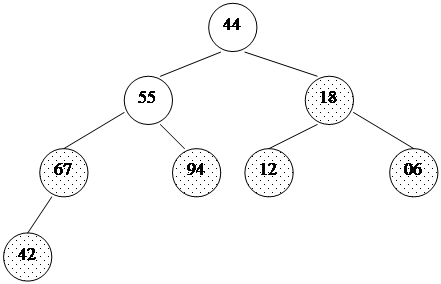
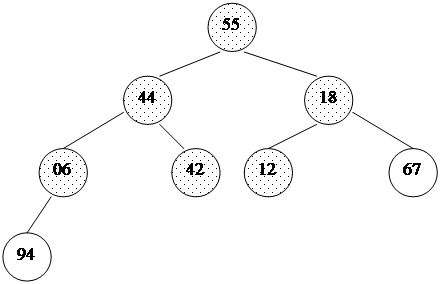
12 сравнили с max(18, 6) = 18 55 сравнили с max(67, 94) = 94
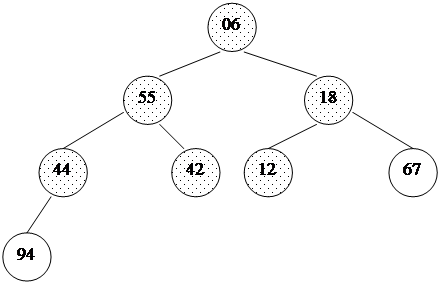
Рис. 18
Рис. 19 Код внешней процедуры сортировки: template<class T>void heapSort(T a[], long size) { long i; T temp; // строим пирамиду for(i=size/2-1; i >= 0; i--) downHeap(a, i, size-1); // теперь a[0]...a[size-1] пирамида for(i=size-1; i > 0; i--) { temp=a[i]; a[i]=a[0]; a[0]=temp; // меняем первый с последним downHeap(a, 0, i-1); // восстанавливаем пирамидальность a[0]...a[i-1 ] }}Каково быстродействие получившегося алгоритма? Построение пирамиды занимает O(n log n) операций, причем более точная оценка дает даже O(n) за счет того, что реальное время выполнения этой процедуры зависит от высоты уже созданной части пирамиды. Вторая фаза занимает O(n log n) времени: O(n) раз берется максимум и происходит просеивание бывшего последнего элемента. Плюсом является стабильность метода: среднее число пересылок (n log n)/2, и отклонения от этого значения сравнительно малы. Пирамидальная сортировка не использует дополнительной памяти. Метод не является устойчивым: по ходу работы массив так "перетряхивается", что исходный порядок элементов может измениться случайным образом. Поведение неестественно: частичная упорядоченность массива никак не учитывается.
Обменяли 94 и 42, забыли о 94 Просеяли 42 сквозь 67, 55 Обменяли 06 и 67, забыли о 67 Просеяли 06 сквозь 55, 44 Рис. 20 Быстрая сортировка Этот метод был разработан более 40 лет назад. Это наиболее широко применяемый и один из самых эффективных алгоритмов. Метод основан на подходе "разделяй-и-властвуй". Общая схема такова: 1) из массива выбирается некоторый опорный элемент a[i]; 2) запускается процедура разделения массива, которая перемещает все ключи, меньшие либо равные a[i], влево от него, а все ключи, большие либо равные a[i] - вправо, 3) теперь массив состоит из двух подмножеств, причем левое меньше либо равно правому (рис.21);
Рис. 21 4) для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру. В конце получится полностью отсортированная последовательность. Далее алгоритм будет рассмотрен подробнее. Разделение массива На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение. 1. Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности. 2. Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p. 3. Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам. 4. Повторяем шаг 3, пока i <= j. Рассмотрим работу процедуры для массива a[0]...a[6] и опорного элемента p = a[3]. Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено (рис. 22).
Исходное положение указателей
Рис. 22 Общий алгоритм Псевдокод. quickSort (массив a, верхняя граница N) { Выбрать опорный элемент p - середину массива Разделить массив по этому элементу Если подмассив слева от p содержит более одного элемента, вызвать quickSort для него. Если подмассив справа от p содержит более одного элемента, вызвать quickSort для него. }
Реализация на языке Си. template<class T>void quickSortR(T* a, long N) {// На входе - массив a[], a[N] - его последний элемент. long i = 0, j = N; // поставить указатели на исходные места T temp, p; p = a[ N>>1 ]; // центральный элемент do { // процедура разделения while (a[i] < p) i++; while (a[j] > p) j--; if (i <= j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while (i<=j); // рекурсивные вызовы, если есть что сортировать if (j > 0) quickSortR(a, j); if (N > i) quickSortR(a+i, N-i);}Каждое разделение требует, очевидно, О(n) операций. Количество шагов деления (глубина рекурсии) составляет приблизительно log n, если массив делится на более-менее равные части. Таким образом, общее быстродействие: O(n log n), что и имеет место на практике. Однако, возможен случай таких входных данных, на которых алгоритм будет работать за O(n2) операций. Такое происходит, если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности. Если данные взяты случайно, вероятность этого равна 2/n. И эта вероятность должна реализовываться на каждом шаге. Метод неустойчив. Поведение довольно естественно, если учесть, что при частичной упорядоченности повышаются шансы разделения массива на более равные части. Сортировка использует дополнительную память, так как приблизительная глубина рекурсии составляет O(log n), а данные о рекурсивных подвызовах каждый раз добавляются в стек.
Модификации кода и метода Во-первых, из-за рекурсии и других "накладных расходов" Quicksort может оказаться не столь уж быстрой для коротких массивов. Поэтому, если в массиве меньше CUTOFF элементов (константа зависит от реализации, обычно равна от 3 до 40), вызывается сортировка вставками. Увеличение скорости может составлять до 15%. Для проведения метода в жизнь можно модифицировать функцию quickSortR, заменив последние 2 строки на if (j > CUTOFF) quickSortR(a, j); if (N > i + CUTOFF) quickSortR(a+i, N-i);Таким образом, массивы из CUTOFF элементов и меньше досортировываться не будут, и в конце работы quickSortR() массив разделится на последовательные части из <=CUTOFF элементов, отсортированные друг относительно друга. Близкие элементы имеют близкие позиции, поэтому, аналогично сортировке Шелла, вызывается insertSort(), которая доводит процесс до конца. template<class T>void qsortR(T *a, long size) { quickSortR(a, size-1); insertSort(a, size); // insertSortGuarded быстрее, но нужна функция setmax()}Во-вторых, в случае явной рекурсии, как в программе выше, в стеке сохраняются не только границы подмассивов, но и ряд совершенно ненужных параметров, таких как локальные переменные. Если эмулировать стек программно, его размер можно уменьшить в несколько раз. В-третьих, чем на более равные части будет делиться массив, тем лучше. Потому в качестве опорного целесообразно брать средний из трех, а если массив достаточно велик - то из девяти произвольных элементов. В-четвертых, пусть входные последовательности очень плохи для алгоритма. Например, их специально подбирают, чтобы средний элемент оказывался каждый раз минимумом. Как сделать QuickSort устойчивой к такому "саботажу"? Очень просто - выбирать в качестве опорного случайный элемент входного массива. Тогда любые неприятные закономерности во входном потоке будут нейтрализованы. Другой вариант - переставить перед сортировкой элементы массива случайным образом. В-пятых, быструю сортировку можно использовать и для двусвязных списков. Единственная проблема при этом - отсутствие непосредственного доступа к случайному элементу. Так что в качестве опорного приходится выбирать первый элемент, и либо надеяться на хорошие исходные данные, либо случайным образом переставить элементы перед сортировкой. При использовании рекурсивного кода, подобного написанному выше, это будет означать n вложенных рекурсивных вызовов функции QuickSort. Каждый рекурсивный вызов означает сохранение информации о текущем положении дел. Таким образом, сортировка требует O(n) дополнительной памяти в стеке. При достаточно большом n такое требование может привести к непредсказуемым последствиям. Для исключения подобной ситуации можно заменить рекурсию на итерации, реализовав стек на основе массива. Процедура разделения будет выполняться в виде цикла. Каждый раз, когда массив делится на две части, в стек будет направляться запрос на сортировку большей из них, а меньшая будет обрабатываться на следующей итерации. Запросы будут выбираться из стека по мере освобождения процедуры разделения от текущих задач. Сортировка заканчивает свою работу, когда запросы кончаются. Псевдокод. Итеративная QuickSort (массив a, размер size) {Положить в стек запрос на сортировку массива от 0 до size-1. do { Взять границы lb и ub текущего массива из стека. do { 1. Произвести операцию разделения над текущим массивом a[lb..ub]. 2. Отправить границы большей из получившихся частей в стек. 3. Передвинуть границы ub, lb чтобы они указывали на меньшую часть. } пока меньшая часть состоит из двух или более элементов } пока в стеке есть запросы}Реализация на языке Си. #define MAXSTACK 2048 // максимальный размер стекаtemplate<class T>void qSortI(T a[], long size) { long i, j; // указатели, участвующие в разделении long lb, ub; //границы сортируемого в цикле фрагмента long lbstack[MAXSTACK], ubstack[MAXSTACK]; // стек запросов /* каждый запрос задается парой значений, а именно: левой(lbstack) и правой(ubstack) границами промежутка*/ long stackpos = 1; // текущая позиция стека long ppos; // середина массива T pivot; // опорный элемент T temp; lbstack[1] = 0; ubstack[1] = size-1; do { lb = lbstack[ stackpos ]; // Взять границы lb и ub текущего массива из стека ub = ubstack[ stackpos ]; stackpos--; do { ppos = (lb + ub) >> 1; // Шаг 1. Разделение по элементу pivot i = lb; j = ub; pivot = a[ppos]; do { while (a[i] < pivot) i++; while (pivot < a[j]) j--; if (i <= j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while (i <= j);/*Сейчас указатель i указывает на начало правого подмассива, j - на конец левого (см. иллюстрацию выше). Возможен случай, когда указатель i или j выходит за границу массива Шаги 2, 3. Отправляем большую часть в стек и двигаем lb, ub */ if (i < ppos) { // правая часть больше if (i < ub) { // если в ней больше 1 элемента - нужно stackpos++; // сортировать, запрос в стек lbstack[ stackpos ] = i; ubstack[ stackpos ] = ub; } ub = j; // следующая итерация разделения будет работать с левой частью } else { // левая часть больше if (j > lb) { stackpos++; lbstack[ stackpos ] = lb; ubstack[ stackpos ] = j; } lb = i; } } while (lb < ub); // пока в меньшей части более 1 элемента } while (stackpos!= 0); // пока есть запросы в стеке}Размер стека при такой реализации всегда имеет порядок O(log n), так что указанного в MAXSTACK значения хватает с лихвой.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-09; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.190 (0.145 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 2
2
 2
2
 1
1

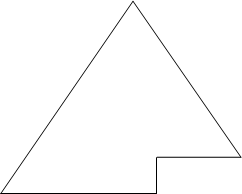 при этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо, т.е форма пирамиды имеет приблизительно такой вид, как на рис. 16:
при этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо, т.е форма пирамиды имеет приблизительно такой вид, как на рис. 16: