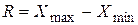Таким образом, R =
Определение размеров классов.
Для большей наглядности поведения изучаемого показателя, процесса, явления количество интервалов должно быть от 5 до 20. Размер класса можно определить путем деления размаха на выбранное удобное число интервалов. Можно наоборот размах разделить на несколько удобных значений размеров классов и выбрать тот, который дает нужное их количество.
Например, определим по второму способу размер класса, если R = 0,37, n = 50
0,37 ׃ 0,05 = 7,4;
0,37 ׃ 0,02 = 18,5;
0,37 ׃ 0,10 = 3,7.
Таким образом, в первом случае получили, округлив - 7, во втором - 19, в третьем – 4 класса. Между 5 и 20 имеется два значения: 7 и 19. Выбираем 7 интервалов, так как, если возникают две возможности, используют более узкий интервал при числе наблюдений 100 и больше, и более широкий - при 99 наблюдениях и меньше. В данном случае 0,05 против 0,02 для 50 наблюдений.
Используя вышеприведенный пример, определить число классов и размер интервала для данных по молоку.
1.3 Заполнение таблицы частот (табл. 3).
1.3.1 Определяя классы, необходимо правильно выбрать минимальное значение. В нашем случае его лучше округлить до 2,500, затем прибавить найденный размер класса. Начало каждого класса должно быть на одну долю больше конца предыдущего класса, для того чтобы выборочные значения не могли принадлежать сразу двум соседним классам.
Например, если min = 45,25, а интервал =0,05, то:
1 класс 45,25 – 45,30; либо 1 класс 45,250 – 45,300;
2 класс 45,31 – 45,35 и т.д., 2 класс 45,301 – 45,350 и т.д.
1.3.2 Определяя середину класса, долю перехода из класса в класс не учитывают, то есть для первого класса суммируют оба значения и делят пополам, а для остальных берут максимальные значения предыдущего и данного класса.
Например,
1 класс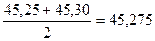 
;
2 класс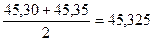 
и т.д.
1.3.3 Используя вышеуказанный пример, заполнить таблицу частот содержания белка в молоке.
Таблица 3 – Таблица частот
| Номер класса | Класс | Середина класса | Подсчет частот | Частота ƒ |
| Итого |
Построение гистограммы
2.1 Используя данные таблицы частот и п 2.2 общих положений, построить гистограмму, показывающую распределение содержания белка в молоке, поступающего на молочный завод.
2.2 Рядом с гистограммой нанести информационные данные.
2.3 Нанести на гистограмму границы допусков в виде вертикалей, проходящих через предельные значения на оси абсцисс.
2.4 Нанести на гистограмму линию, показывающую среднее значение выборки.
Для получения более точного значения используют формулу:
.
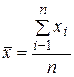Для ускорения расчетов среднее значение выборки считают по формуле:
,
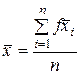где ƒ – количество частот (выборочных значений) в классе;
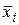-среднее значение класса.
Для второго варианта расчета средней арифметической удобно использовать следующую таблицу
Таблица 4 Данные для расчета средней арифметической
| Номер класса | Середина класса 
| Частота ƒ | ƒ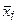 
| 
|
|
| ||||
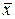
| Итого | n = | Σ = |
2.5 Определить тип гистограммы и есть ли смещение относительно центра размаха.
2.6 Определить количество брака и по содержанию белка сделать вывод о качестве молока – сырья, поступающего на молочный завод.
План самостоятельной работы
1 Выбрать вариант задания (приложение А), который соответствует номеру фамилии студента в списке группы в алфавитном порядке.
2 Рассчитать данные и построить гистограмму;
3 Нанести на гистограмму все необходимые данные;
4 Сделать выводы о характере распределения и качестве продукции.
|
| Поделиться: |
