
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение предела последовательности и функции.Содержание книги
Поиск на нашем сайте
«Предел последовательности» Множество действительных чисел, пронумерованных с помощью натуральных чисел:
Например, Определение. Число Обозначение предела: Если рассмотреть полосу от
Чем меньше число Пример.
* Для того, чтобы лучше понять, что такое предел, представьте следующее. Машина приближается к городу. Для любого заранее заданного расстояния (например
Для некоторых последовательностей предел может не существовать. Так, для последовательности Для последовательности
Простейший пример. Найти предел Решение. Сократим на n. Ответ. Задача 175. Найти предел Решение. Здесь неопределённость типа
Каждая из мелких дробей в числителе и знаменателе стремится к 0, поэтому получается сумма пределов в каждом случае, и тогда
Задача 176. Найти предел Решение. Здесь неопределённость типа
Задача 177. Найти предел Решение. Есть 2 способа. Можно сократить на
А можно сократить на
Ответ. 0. Замечание. Если наоборот, в знаменателе была бы степень больше, чем в числителе, то ответ не 0 а В общем случае, когда степени разные: Задача 178. Найти предел Решение. Здесь неопределённость типа Чтобы свести к дроби, и сокращать как в прошлых примерах, надо сначала домножить на «сопряжённое» выражение, то есть такое где вместо разности сумма, это позволит использовать формулу сокращённого умножения
Теперь можно сократить на первую степень
Задача 179. Найти предел Решение. Здеь домножение и не требуется, а можно сразу сократить на
Задача 180. Найти предел Решение. Можем сразу сократить на
Таблица соответствия недель, задач и номеров практик.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

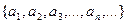 называется числовой последовательностью. Её можно определить также и как функцию
называется числовой последовательностью. Её можно определить также и как функцию 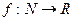 . Графиком в этом случае будет не кривая, а дискретный набор точек.
. Графиком в этом случае будет не кривая, а дискретный набор точек. 
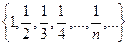 - последовательность.
- последовательность. называется пределом последовательности
называется пределом последовательности 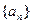 , если:
, если: 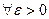
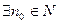 , такое, что
, такое, что 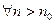 выполняется:
выполняется: 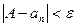 . В этом случае говорится, что последовательность стремится к числу А.
. В этом случае говорится, что последовательность стремится к числу А. 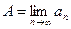 .
.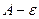 до
до 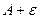 по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:
по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу: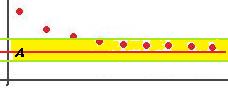
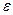 (погрешность меньше) тем больший номер требуется.
(погрешность меньше) тем больший номер требуется.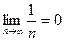 . По определению: если например требуемая точность
. По определению: если например требуемая точность 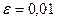 то
то 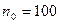 ,
, 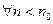 выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.
выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.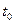 , что в последующие моменты времени
, что в последующие моменты времени 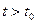 расстояние будет меньше, чем
расстояние будет меньше, чем 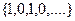 предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа
предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа 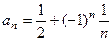 предел равен
предел равен 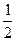 .
.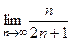 .
.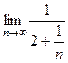 =
= 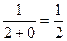 .
.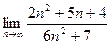 .
. 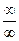 . Вынесем за скобки
. Вынесем за скобки 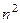 и в числителе, и в знаменателе, с целью сократить на этот множитель.
и в числителе, и в знаменателе, с целью сократить на этот множитель.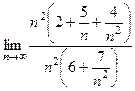 =
= 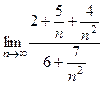
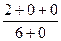 =
= 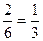 . Ответ.
. Ответ. 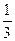 .
.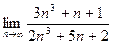 .
. 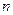 , в прошлой задаче это была 2-я степень, а здесь 3-я.
, в прошлой задаче это была 2-я степень, а здесь 3-я.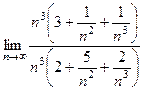 =
= 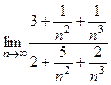 =
= 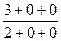 =
= 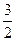 . Ответ.
. Ответ. 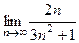 .
.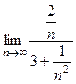 =
= 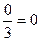 .
.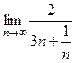 =
= 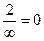 .
. .
. =
= 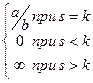 .
.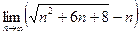 .
.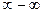 . Будет ошибочно думать, что
. Будет ошибочно думать, что 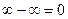 . Так, например, если от нас удаляются 2 объекта со скоростями
. Так, например, если от нас удаляются 2 объекта со скоростями 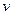 и
и 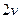 , то не только расстояние от нас до каждого объекта, но и расстояние между ними увеличивается к
, то не только расстояние от нас до каждого объекта, но и расстояние между ними увеличивается к 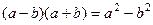 .
.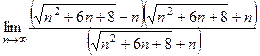 =
= 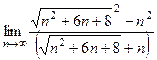 =
=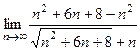 =
= 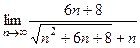 .
.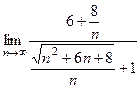 =
= 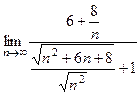 =
= 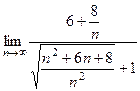 =
= 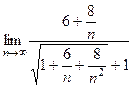 =
= 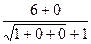 =
= 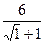 = 3. Ответ. 3.
= 3. Ответ. 3.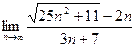 .
.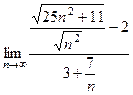 =
= 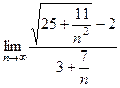 =
= 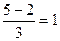 . Ответ. 1.
. Ответ. 1.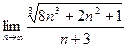 .
.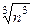 .
.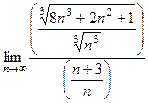 =
= 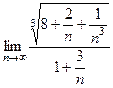 =
=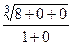 = 2. Ответ. 2.
= 2. Ответ. 2.


