
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм поиска собственных векторов.Стр 1 из 5Следующая ⇒
Практика № 10. Задача 90. Вычислить площадь параллелограмма, образованного векторами Решение. Площадь параллелограмма - значит, надо вычислить модуль векторного произведения
Ответ 92.
Задачи 91 и 92. Векторы a,b выражены через p,q: Задача 91. Найти Решение.
Ответ. 1227. Задача 92. Найти | [a,b] |. Решение. | [a,b] | = |
Ответ.
Задача 93. Найти смешанное произведение трёх векторов:
Решение. Вычислим определитель:
Задача 94. Доказать, что 4 точки: A(1,1,1), B(2,3,1), C(2,4,2), D(3,6,2) лежат в одной плоскости. Решение. Составим 3 вектора AB, AC, AD и докажем, что они лежат в одной плоскости. AB = (1,2,0), AC = (1,3,1), AD = (2,5,1). Определитель Ответ. 4 точки в одной плоскости. Задача 95. Найти объём тетраэдра, вершины которого A(1,1,1), B(2,1,3), C(2,2,4), D(1,2,4). Решение. Объём тетраэдра ровно в 6 раз меньше объёма параллелепипеда с рёбрами AB, AC, AD. Найдём эти векторы, и сначала вычислим объём параллелепипеда с помощью определителя, затем поделим на 6. AB = (1,0,2), AC = (0,1,3), AD = (1,1,3).
Ответ. Объём тетраэдра равен
Линейные операторы Задача 96. Построить матрицу линейного оператора в 2-мерном пространстве, если действие оператора задано таким образом: Решение. Находим, в какие векторы отображаются два базисных вектора: Эти результаты запишем по столбцам: Ответ. Матрица линейного оператора Проверка: Так,
Задача 97. Построить матрицу линейного оператора в 3-мерном пространстве Решение. Отобразим базис 3-мерного пространства.
Ответ. Матрица линейного оператора
Задача 98. Построить матрицу оператора поворота на произвольный угол Решение. Найдём матрицу оператора поворота на угол
Расстояния r1 и r2 здесь равны Ответ. При
При
Задача 99. С помощью линейного оператора поворота плоскости доказать, что скалярное произведение не изменяется при повороте. Решение. Рассмотрим векторы
А теперь скалярно перемножим 2 получившихся вектора:
Учитывая, что 3,4,7,8 слагаемые взаимоуничтожаются, получим:
Ответ: Что и требовалось доказать.
Практика 11 (21.10.2020). Ответ. Собст. число собст. число собст. число
Задача 107. Найти собственные числа и векторы Решение.
Итак, система из 1 уравнения с 3 неизвестными: Тогда
Ещё два уравнения в ней пропорциональны, так что в итоге, у нас есть такое общее решение: Ответ. Кратный корень Корень Проверка. Задача 108. Найти все собственные значения и векторы для линейного оператора, заданного матрицей: Решение. Найдём собственные значения с помощью характеристического уравнения.
Видно, что есть по крайней мере один корень
Затем разделим многочлен
Итак, разделилось без остатка. Таким образом,
Для многочлена 2 степени: Итак, собственные числа: Теперь ищем вектор для каждого из этих чисел. Пусть
Запишем систему, заодно при этом поделив 1-е уравнение на 2.
Из 1-го сразу
Пусть теперь
Из 1-го уравнения сразу очевидно Система:
Пусть теперь
из 1-го уравнения
Ответ.
Практика № 12. 23.10.2020. Задача 109. Найти все собственные значения и векторы для линейного оператора, заданного матрицей: Решение.
откуда
откуда
откуда Тогда ФСР это вектор (1,0,0). Ответ.
Задача 110. Найти все собственные значения и векторы для линейного оператора, заданного матрицей: Решение.
отсюда следует, что
отсюда следует, что
Здесь 2 уравнения. Если вычесть 1-е из 2-го, получим Ответ.
Квадратичные формы. Задача 111. Построить матрицу кв. формы Решение. Распределим поровну коэффициенты:
Ответ: матрица: Задача 112. Построить матрицу квадратичной формы:
Решение. По диагонали коэффициенты при квадратах, а остальные должны быть разделены поровну, то есть Таким образом мы добиваемся, чтобы матрица была симметрической. Ответ. Матрица Проверка.
Приведение к главным осям. Алгоритм: 1. Записать матрицу кв. формы. 2. Найти собственные числа и векторы. 3. Нормировать векторы. 4. Записать формулы перехода от старого к новому базису. 5. Подставить в кв. форму, привести подобные. Задача 113. Квадратичную форму Решение. Сначала построим её матрицу: Характеристическое уравнение
Затем нужно нормировать их, то есть поделить на длину. Итак получили новый ортонормированный базис:
Запишем связь старых и новых координат, новые мы обозначаем
Итак, верны такие формулы: В записи квадратичной формы заменим
Ответ. Кв.форма: Задача 114. Квадратичную форму Решение. Матрица квадратичной формы Найдём собственные числа и векторы. Характеристическое уравнение Собственные числа 5 и 1. Решаем две однородные системы, для каждого
Нормируем этот вектор, то есть делим на его длину, которая составляет Аналогично,
Нормируем его: Как видим, эти векторы ортогональны. Это потому, что матрица оператора симметрична (что и так следует из теоремы 7, см.лекции). Обратите внимание, что этот новый базис - повёрнутый на 450 декартов базис, то есть (1,0) и (0,1). Синим цветом нарисованы векторы (1,0) и (0,1) а красным
При таком преобразовании плоскости не искажаются площади фигур. Если бы мы не нормировали векторы, то при линейном преобразовании искажались бы площади, коэффициенты квадратичной формы в новом базисе не получились бы равны собственным числам
Обозначим новые координаты
Если мы подставим эти
Собственные числа, как видим, как раз и оказались в роли коэффициентов при квадратах. Ответ.
Задача 115. Привести к главным осям квадратичную форму: Q(x,y) = 14 Решение. Матрица:
Ищем собственные векторы. Пусть уравнения в такой системе пропорциональны, ранг равен не 2, а 1. Фактически, здесь одно уравнение: Можно в качестве ФСР принять вектор (3,4). Однако его ещё надо нормировать. Длина равна Итак, нормированный собственный вектор
Пусть уравнения пропорциональны, ранг равен 1. Фактически, здесь одно уравнение: Можно в качестве ФСР принять вектор Итак, новый базис состоит из векторов Переход к новым координатам:
Если подставить эти выражения в 14
Ответ.
Практика 13. Аналитическая геометрия. Прямая на плоскости Плоскость в пространстве. Задача 131. Построить уравнение плоскости, проходящей через точку A(1,2,3) перпендикулярно вектору Решение. Для произвольной точки
Ответ. Уравнение плоскости Замечание. Второй способ. Если мы уже знаем из теории, что координаты нормали это и есть коэффициенты A,B,C в уравнении плоскости, то можно сразу записать Задача 132. Построить уравнение плоскости по точке (2,2,8) и перпендикуляру (3,3,7). Решение. Как и в прошлой задаче, берём произвольную точку Ответ.
Задача 133. Построить уравнение плоскости, проходящей через (0,0,0) параллельно 2 направляющим (1,1,2) и (2,1,3). Решение. Вектор от начала координат до произвольной точки Ответ.
Практика 14. Задача 134. Построить уравнение плоскости по точке Решение. Возьмём вектор
Из этого следует Ответ.
Задача 135. Построить уравнение плоскости по трём точкам. А(1,2,3), В(3,5,7), С(4,5,6). Решение. Здесь можно одну из точек, например А, рассматривать в качестве основной, а две другие помогут найти 2 направляющих вектора: АВ и АС. АВ = (2,3,4), АС = (3,3,3).
Для удобства вычислений, вынесли из определителя коэффициент 3. Можно сразу сократить на него правую и левую часть. Итак,
Сократим ещё на Ответ.
Задача 136. Найти расстояние от точки M1 (3,1,5) до плоскости Решение. По формуле
Ответ. Задача 137. Найти угол между двумя плоскостями:
Решение. Нормали к этим плоскостям: Нормали не коллинеарны, то есть плоскости не параллельны, значит, они действительно пересекаются по какой-то прямой, и между ними есть какой-то угол.
Кстати, константа в уравнении одной из плоскостей никак не влияет на ответ, так как параллельный перенос плоскости не влияет на угол, который она образует с другой плоскостью. Ответ. Задача 138. Через точку Решение. Если плоскость содержит ось и точку, то в ней по крайней мере содержится начало координат, и 2 такие направляющих: один проведён от (0,0,0) к точке А затем мы найдём угол между их нормалями. Эти плоскости можно представить так: две наклонные части крыши. Плоскость, перпендикулярная линии ОМ, не горизонтальна, так что угол между двумя частями такой крыши вовсе не 90 градусов. Чем более пологая крыша, тем ближе этот угол к 180, а чем более крутая, тем ближе к 90. Плоскость, перпендикулярная стыковочной линии крыши, а именно линии ОМ, показана жёлтым цветом.
Строим уравнение 1-й плоскости. Возьмём 3-й вектор, проведённый к какой-то произвольной точке
Нормаль к этой плоскости Строим уравнение 2-й плоскости. Аналогично, только (0,1,0).
Нормаль к этой плоскости Известно, что Тогда Замечание. Если бы надо было найти косинус наименьшего угла, то есть острого, то должны были бы рассматривать модуль
Вообще же, всегда имеется два угла, Прямая в пространстве Практика 15 Задача 143. Доказать, что две прямые в пространстве
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 53; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.208.117 (0.242 с.) |
 , если
, если  ,
,  , угол между p,q равен
, угол между p,q равен  .
.  =
=  =
=  =
=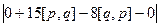 =
= 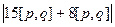 =
=  =
=  =
= = 92.
= 92.  ,
, 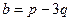 .
.  , угол между ними 600.
, угол между ними 600. .
. 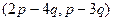 =
=  =
=  =
=  =
= =
=  = 1227.
= 1227. |= |
|= | 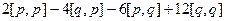 | = |
| = | 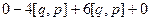 | = |
| = |  | =
| = 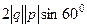 =
=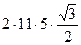 =
=  .
. .
. =
=  = 25. Ответ.
= 25. Ответ. 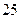 .
.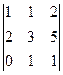 = 0 так как 3 строка есть сумма 1-й и 2-й.
= 0 так как 3 строка есть сумма 1-й и 2-й. =
=  ,
,  .
. .
. .
. ,
, 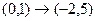 .
. .
. . То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу.
. То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу. но ведь и по исходным формулам
но ведь и по исходным формулам 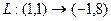 .
.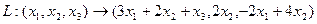

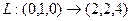
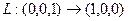
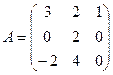 .
. .
.
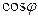 и
и  . Красным показаны образы базисных векторов. Получаем матрицу
. Красным показаны образы базисных векторов. Получаем матрицу  .
.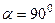 получится
получится  Действие оператора на любой вектор задаётся матрицей так:
Действие оператора на любой вектор задаётся матрицей так:  - любой вектор поворачивается на 90 градусов.
- любой вектор поворачивается на 90 градусов. матрица
матрица  , и действительно, умножение на такую матрицу переводит любой вектор
, и действительно, умножение на такую матрицу переводит любой вектор 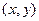 в
в 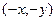 .
.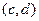 . Их скалярное произведение равно
. Их скалярное произведение равно  . теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол
. теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол  =
= 
 =
= 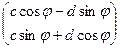
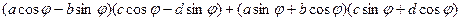 =
= +
+
 =
= 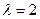 собст. вектор (1,0,0),
собст. вектор (1,0,0),  собст. вектор (1,1,0),
собст. вектор (1,1,0), собст. вектор (1,1,1).
собст. вектор (1,1,1).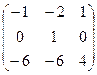
 разложим по 2-й строке:
разложим по 2-й строке: =
=  что сводится к
что сводится к , первый корень и так виден и равен 1, у второго выражения найдём корни, например, через дискриминант, получаем 1 и 2. Итак,
, первый корень и так виден и равен 1, у второго выражения найдём корни, например, через дискриминант, получаем 1 и 2. Итак,  , корни 1,1,2, они же собственные числа. Два характеристических корня совпали (1 это корень кратности 2). Теперь ищем собственные векторы.
, корни 1,1,2, они же собственные числа. Два характеристических корня совпали (1 это корень кратности 2). Теперь ищем собственные векторы.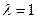 .
. , если в такой системе уравнений вычесть из 3-го уравнения утроенное 1-е, то 3-е обнулится, и в итоге ранг системы равен 1. То есть мы видим, что в случае корня кратности 2, ранг понизился сразу на 2 пункта, здесь будет 2 свободных неизвестных.
, если в такой системе уравнений вычесть из 3-го уравнения утроенное 1-е, то 3-е обнулится, и в итоге ранг системы равен 1. То есть мы видим, что в случае корня кратности 2, ранг понизился сразу на 2 пункта, здесь будет 2 свободных неизвестных. .
. , свободные переменные
, свободные переменные  поочерёдно принимают значение 1, ФСР из двух векторов: (1,0,2) (0,1,2).
поочерёдно принимают значение 1, ФСР из двух векторов: (1,0,2) (0,1,2). , при этом сразу замечаем, что из 2-го уравнения будет следовать
, при этом сразу замечаем, что из 2-го уравнения будет следовать 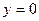 , поэтому в остальных уравнениях его сразу не пишем. Однородная система:
, поэтому в остальных уравнениях его сразу не пишем. Однородная система: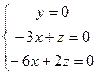
 . ФСР вектор (1,0,3).
. ФСР вектор (1,0,3).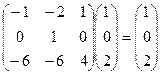 ,
, 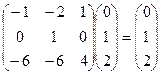 ,
, 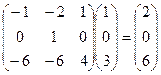 .
.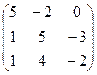
 сводится к
сводится к 
 на
на 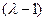 , получим крадратичное уравнение и там найдём ещё 2 корня.
, получим крадратичное уравнение и там найдём ещё 2 корня.
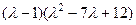 .
. . Корни
. Корни 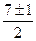 , т.е. 3 и 4.
, т.е. 3 и 4.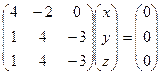 здесь сразу видим, что 2 и 3 строка одинаковы, то есть 3-е уравнение копия 2-го, так что в системе фактически не 3, а 2 уравнения.
здесь сразу видим, что 2 и 3 строка одинаковы, то есть 3-е уравнение копия 2-го, так что в системе фактически не 3, а 2 уравнения.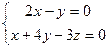
 , подставляя во 2-е, можно также и
, подставляя во 2-е, можно также и 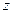 выразить через
выразить через  :
:  , т.е.
, т.е.  . При этом
. При этом  . ФСР это вектор (1,2,3).
. ФСР это вектор (1,2,3).
 .
. Если учесть
Если учесть 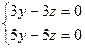 так что очевидно, что и
так что очевидно, что и  . ФСР (1,1,1).
. ФСР (1,1,1).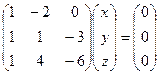 Система:
Система: 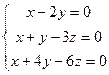
 , подставим эту информацию во 2-е и 3-е.
, подставим эту информацию во 2-е и 3-е. значит
значит  .
.  сводится к уравнению
сводится к уравнению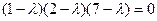 , корни которого:
, корни которого: 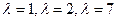 .
.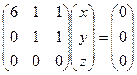 , система
, система 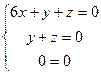
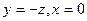 , ФСР это вектор
, ФСР это вектор  .
.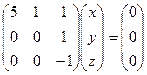 , система
, система 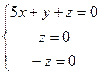
 , ФСР это вектор
, ФСР это вектор 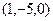 .
. .
. , система
, система 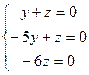
 , а значит и
, а значит и 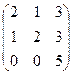
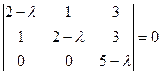 сведём к уравнению.
сведём к уравнению.


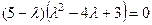 . Один корень, очевидно,
. Один корень, очевидно, 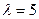 , два других найдём, решим квадратное уравнение (через дискриминант либо по теореме Виета). Получим
, два других найдём, решим квадратное уравнение (через дискриминант либо по теореме Виета). Получим  .
. система
система 
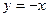 . Тогда вектор
. Тогда вектор  .
.  система
система 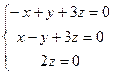
 . Тогда вектор (1,1,0).
. Тогда вектор (1,1,0). 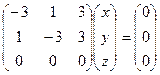 система
система 
 , то есть
, то есть  , в итоге
, в итоге  , и
, и 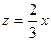 . Если присвоить
. Если присвоить 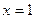 , получим вектор
, получим вектор  . Впрочем, чтобы не было дробей, можем увеличить в 3 раза, и рассматривать собственный вектор (3,3,2).
. Впрочем, чтобы не было дробей, можем увеличить в 3 раза, и рассматривать собственный вектор (3,3,2).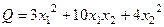 .
. . Каждый коэффициент, стоящий при
. Каждый коэффициент, стоящий при  , запишем на место
, запишем на место  .
.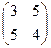 .
.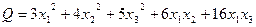 .
. 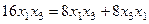 .
.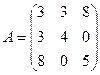 .
. =
=  .
. привести к главным осям.
привести к главным осям. .
.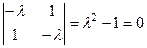 , собственные числа
, собственные числа 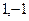 . Ищем собственные векторы для каждого из них.
. Ищем собственные векторы для каждого из них. ,
, 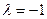 :
:  ,
, 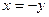 , собственный вектор
, собственный вектор 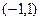 .
. и
и  .
.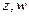 .
. здесь надо вспомнить, что для нахождения новых координат мы решали систему уравнений, где основная матрица - это «матрица перехода», у которой в столбцах векторы нового базиса.
здесь надо вспомнить, что для нахождения новых координат мы решали систему уравнений, где основная матрица - это «матрица перехода», у которой в столбцах векторы нового базиса. ,
, 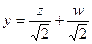 .
. , и останутся только квадраты, причём коэффициентами как раз и окажутся собственные числа.
, и останутся только квадраты, причём коэффициентами как раз и окажутся собственные числа.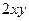 =
= 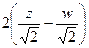
 =
=  =
=  .
.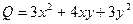 привести к главным осям.
привести к главным осям.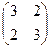 .
. 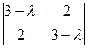 =
= 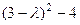 =
=  =
= 
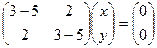 ,
,  , ранг системы = 1, остаётся одно уравнение
, ранг системы = 1, остаётся одно уравнение 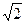 . Получаем
. Получаем 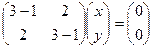 ,
, 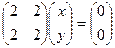 , ранг системы = 1, остаётся одно уравнение
, ранг системы = 1, остаётся одно уравнение 
 - отсюда, умножив матрицу на столбец, можно записать формулы связи старых и новых координат:
- отсюда, умножив матрицу на столбец, можно записать формулы связи старых и новых координат: 
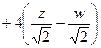
 =
=

 =
= =
= 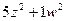 .
.  , новый базис
, новый базис  +24
+24  +21
+21  .
. . Ищем собственные числа и векторы.
. Ищем собственные числа и векторы.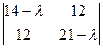 =
=  =
=  .
. ,
, 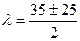 , корни 30 и 5.
, корни 30 и 5.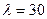 .
. 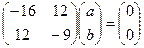 ,
, 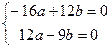
 .
. 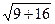 = 5.
= 5. .
. ,
, 
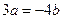 .
.  . Длина равна 5. Нормированный собственный вектор
. Длина равна 5. Нормированный собственный вектор  .
. , т.е.
, т.е.  ,
, 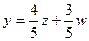 .
. 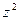 +5
+5 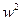 .
. + 24
+ 24 
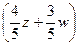 + 21
+ 21  =
=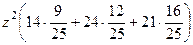 +
+  +
+ =
=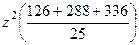 +
+  +
+  =
=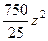 +
+  +
+  = 30
= 30  30
30 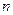 (1,4,2)
(1,4,2)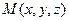 в плоскости, вектор
в плоскости, вектор  с координатами
с координатами  ортогонален
ортогонален  . Их скалярное произведение 0. Тогда
. Их скалярное произведение 0. Тогда 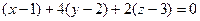 , т.е.
, т.е. .
. , а затем найти неизвестную D, используя условие, что точка (1,2,3) принадлежит плоскости:
, а затем найти неизвестную D, используя условие, что точка (1,2,3) принадлежит плоскости: 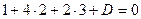 , откуда
, откуда 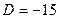 .
. ортогонален вектору
ортогонален вектору 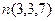 . Тогда
. Тогда  из чего следует
из чего следует  .
. , который сам имеет координаты
, который сам имеет координаты  =
=  .
. и двум направляющим векторам
и двум направляющим векторам 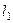 (4,2,3) и
(4,2,3) и  .
. в плоскости, тогда 3 вектора, а именно
в плоскости, тогда 3 вектора, а именно  ,
,  =
=  =
= 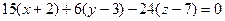 .
. . Такое уравнение можно сократить на 3, и получается
. Такое уравнение можно сократить на 3, и получается  .
.


 .
. 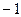 , получим
, получим 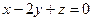 .
.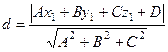 получаем, что
получаем, что =
=  =
=  =
=  .
. .
. и
и 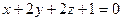 .
.  и
и  .
.  =
=  =
=  .
. , что приблизительно составляет 83,6 градусов.
, что приблизительно составляет 83,6 градусов.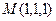 и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти тупой угол между этими плоскостями.
и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти тупой угол между этими плоскостями. , а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.
, а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.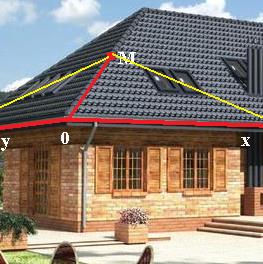
 ,
, 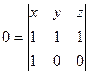 =
=  =
=  .
. .
. =
=  =
=  .
. .
. .
.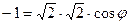 , т.е.
, т.е. 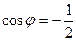 , угол 120 градусов.
, угол 120 градусов.  , чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.
, чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.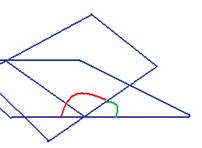
 . В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как
. В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как 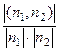 либо
либо 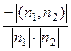 . Ответ.
. Ответ. 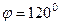 .
.


