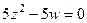Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Блок задач на поиск пересечений.
Задача 142. Доказать, что прямая Решение. Если прямая пересекает ось Если бы первые две дроби после такой подстановки оказались не равны, то это бы означало, что нет пересечения с осью Ответ. (0,0,1). Замечание. Если бы прямая и ось
Практика 15 Задача 143. Доказать, что две прямые в пространстве
Решение. Если у них естьь общая точка, то можно приравнять
Преобразуем методом Гаусса. От 2-й строки отнимем утроенную 1-ю, а к 3-й прибавим 4-кратную 1-ю.
Впрочем, можно было решить систему ещё быстрее, если сложить 2 и 3 уравнения, тогда сразу бы получилось Затем подставить получим одни и те же значения для
Ответ. Точка пересечения (1,1,2). Задача 144. Найти точку пересечения плоскости Решение. Запишем прямую с помощью параметрических уравнений:
Подставим эти выражения в уравнение плоскости, чтобы найти, при каком значении
Ответ. Точка пересечения Нахождение углов и расстояний. Задача 145. Найти угол между прямой и плоскостью Решение. Формула: Направляющий к прямой Их скалярное произведение равно 9. Модули векторов равны Приблизительно представим, какой это угол. Если бы было
Но в данном случае дробь чуть меньше, а угол составляет около 79 градусов. Ответ.
Задача 146. Вычислить расстояние от точки Решение. Во-первых, можно заметить, что точка не принадлежит прямой. Если подставить Применим формулу Точка
Его модуль равен
Модуль этого вектора равен Задача 147. Найти проекцию точки Решение. Представим прямую с помощью параметрических уравнений.
Вектор
Тогда при данном
Ответ. Проекция - точка Замечание. Расстояние от точки Задача 148. Даны три точки А(1,1,1),В(2,2,3),С(2,1,2). Вывести уравнение прямой, содержащей АВ, и найти расстояние от точки С до этой прямой (высота треугольника АВС). Решение. Вектор АВ (1,1,2) можем принять в качестве направляющего для этой прямой. Он отложен от точки А(1,1,1). Тогда канонические уравнения прямой:
Расстояние в данной ситуации, в пространстве, надо искать по формуле Здесь точки А,С играют ту же роль, что 2-я сторона параллелограмма: АС=(1,0,1). Векторное произведение:
Модуль вектора Ответ. Задача 149. Доказать, что две прямые в пространстве:
Решение. Решая систему уравнений (как в задаче 133) здесь мы обнаружим, что система несовместна.
прибавим ко 2-й строке 1-ю, а от 3-й отнимем 1-ю.
2-е и 3-е уравнения противоречат друг другу. Система не имеет решений, значит, эти 2 прямые не имеют ни одной общей точки.
Так как направляющие векторы Найдём расстояние между ними. Точку на каждой прямой можно найти, присваивая Вычисляем по формуле Смешанное произведение с помощью определителя.
=
Модуль векторного произведения равен
Задача 150. Заданы 2 прямые в пространстве, одна - своими параметрическими уравнениями, а другая как пересечение пары плоскостей:
Доказать, что эти прямые параллельны.
Решение. Найдём направляющие векторы этих прямых и докажем, что они коллинеарны. Для 1-й прямой надо просто выбрать коэффициенты при Для 2-й прямой надо искать направляющий как векторное произведение нормалей к двум плоскостям.
Векторы
Итак, прямые параллельны. Задача 151. Заданы 2 прямые в пространстве:
Доказать, что эти прямые параллельны, и найти уравнение плоскости, содержащей их. Решение. Во-первых, направляющие векторы (1,1,2) и (2,2,4), что видно из коэффициентов при Построим канонические уравнения первой прямой, выразив параметр
При Точка в плоскости, например, M1. Итак, проведём плоскость через точку M1(1,2,3) и 2 направляющих:
Ответ.
На повторение прямых в плоскости, для контрольных работ: Задача 152. Найти: а) уравнение прямой, проходящей через точку б) уравнение прямой, проходящей через точку в) точку пересечения этих прямых. Решение. а) прямая б)
в) Ищем их пересечение, решая систему.
Из 2-го вычтем утроенное 1-е, будет Ответ.
Практика 16. Кривые.
Полярная система координат. Кроме пары чисел
Так как
Задача 153. Построить уравнение прямой Решение. На чертеже видно, что чем больше угол наклона, тем больше расстояние. При
В уравнении Замечание. При Ответ. Задача 154. Построить уравнение прямой Решение. В уравнении Ответ. Задача 155. Построить уравнение окружности Решение.
Замечание. Здесь снова, как было в позапрошлой задаче, если луч направлен во 2-ю или 3-ю четверть, при этом косинус отрицателен, а значит, мы попадаем в противоположную сторону - снова на ту же окружность, и она чертится 2-й раз. Ответ. Задача 156. Построить уравнение линии
Решение. В уравнении заменим обе переменные
Ответ.
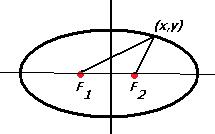
Определение эллипса. Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний до двух фиксированных точек постоянна.
Задача 157. Доказать, что кривая является эллипсом, найти каноническое уравнение, центр и полуоси. Решение. Выделим полный квадрат по каждой переменной.
Ответ. Центр Чертёж:
Задача 158. Доказать, что кривая является эллипсом, найти каноническое уравнение, центр и полуоси, построить чертёж. Решение. Здесь в уравнении есть произведение Находим собственные числа и векторы.
Собственные числа 1 и 9. Ищем собственные векторы.
Нормируем его, то есть делим на длину, которая здесь
Это единичный вектор в 1-й четверти, получающийся поворотом (1,0) на 45 градусов.
Нормируем его, получаем Это вектор во 2-й четверти, получающийся поворотом (0,1) на 45 градусов. Запишем формулы перехода от одного базиса к другому:
Если подставить эти выражения в исходное уравнение, то после приведения подобных исчезнут выражения, содержащие разные переменные
в линейной форме
Итак, как мы видим, коэффициентами как раз и оказались 9 и 1, то есть собственные числа матрицы этой квадратичной формы. Заметим, что 1-й степени
Центр
Если Итак, центр - точка (1,1). В направлении первого вектора нового базиса, а именно Ответ. Центр Чертёж:
Задача 159 (теоретическая). Доказательство (вывод) уравнения эллипса. Выведем уравнение кривой, удовлетворяющей этому свойству ( Пусть фокусы расположены в точках Фокус F2 наоборот, расположен ближе к точке на чертеже то есть катет на оси Ox равен Выясним, какой именно константе равна величина Заметим, что если оба корня возвести в квадрат, то они будут отличаться только одним слагаемым, а именно
Но ведь Тогда мы знаем и разность: Итак, получили систему, из которой можно определить каждое
Сложив эти 2 равенства, получим а вычитая второе из 1-го, Сопоставим выражения, изначально полученные по теореме Пифагора, с этими выражениями:
Рассмотрим вершину
Но ведь он является гипотенузой треугольника, один катет которого это малая полуось (длина Итак, каноническое уравнение эллипса:
Задача 160. Доказать, что однополостный гиперболоид Чертёж:
Решение. Рассмотрим вертикальную плоскость, проходящую через его вершину, например,
Практика 17. Задача 161. Доказать, что кривая является параболой, найти каноническое уравнение, построить чертёж. Решение. Сначала построим матрицу квадратичной формы.
Найдём собственные значения и векторы.
корни Ищем собственные векторы. Для
Нормируем этот вектор: Для
Итак, новый базис: Составим матрицу перехода, записав их по столбцам. Пусть новые координаты будут обозначены
Подставим эти две формулы перехода к новым координатам в выражение
+
+
| Поделиться:
| |
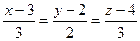 пересекает ось
пересекает ось  и найти точку пересечения.
и найти точку пересечения. . Если в первые две дроби вместо
. Если в первые две дроби вместо  подставить 0, то получим
подставить 0, то получим  . Тогда
. Тогда 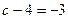 , т.е.
, т.е.  .
.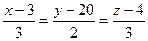 получили бы
получили бы 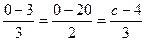 , но ведь
, но ведь  , т.е. противоречие уже в первых дробях, независимо от
, т.е. противоречие уже в первых дробях, независимо от 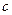 .
. и
и 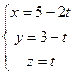 пересекаются, и найти точку пересечения.
пересекаются, и найти точку пересечения. из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах
из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах  , а во вторых
, а во вторых 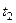 .
. перенесём все
перенесём все  расширенная матрица:
расширенная матрица: 
 т.е.
т.е.  то есть сразу же
то есть сразу же  из 2-го и 3-го уравнений, и они не противоречат друг другу. Система совместна, ранги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем
из 2-го и 3-го уравнений, и они не противоречат друг другу. Система совместна, ранги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем  , т.е.
, т.е.  .
.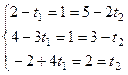 , т.к.
, т.к.  и
и 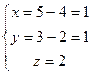
 и прямой
и прямой  .
.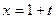 ,
,  ,
,  .
.  оно выполняется.
оно выполняется. 


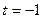 . Тогда
. Тогда 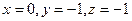 .
. .
.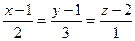
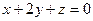 .
.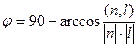 .
. , нормаль к плоскости
, нормаль к плоскости  .
.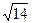 и
и  .
.  .
.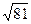 вместо
вместо 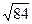 то было бы
то было бы 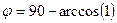 = 90.
= 90.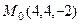 до прямой
до прямой 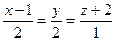 в пространстве.
в пространстве.  ,
,  .
. .
.  на прямой ищется из таких соображений: все дроби в каноническим уравнении приравняем к 0, тогда
на прямой ищется из таких соображений: все дроби в каноническим уравнении приравняем к 0, тогда 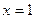 ,
, 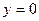 ,
, 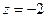 .
.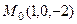 .
.  . Направляющий вектор состоит из чисел в знаменателях в канонических уравнениях:
. Направляющий вектор состоит из чисел в знаменателях в канонических уравнениях:  .
. 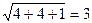 . Векторное произведение:
. Векторное произведение: =
=  =
=  .
. . Ответ.
. Ответ. 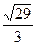 .
. на прямую
на прямую  .
.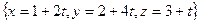 . Направляющий здесь
. Направляющий здесь  , начальная точка
, начальная точка 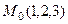 . Теперь можно найти такое время
. Теперь можно найти такое время 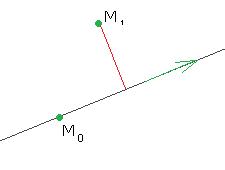
 ортогонален
ортогонален 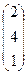 , то есть их скалырное произведение равно 0. Тогда
, то есть их скалырное произведение равно 0. Тогда
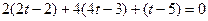
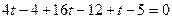
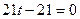
 .
. , то есть точка
, то есть точка  .
. , то есть
, то есть 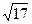 . Это 2-й способ вычислить расстояние от точки до прямой, через проекцию, в отличие от метода прошлой задачи.
. Это 2-й способ вычислить расстояние от точки до прямой, через проекцию, в отличие от метода прошлой задачи.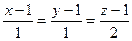 .
.
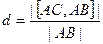 .
. в прошлой задаче.
в прошлой задаче. .
. =
=  =
= 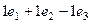 .
.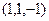 равен
равен  . Тогда результат:
. Тогда результат: 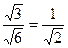 .
.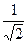 .
. и
и  скрещивающиеся, и найти расстояние между ними.
скрещивающиеся, и найти расстояние между ними.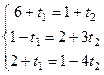
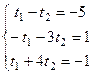 матрица:
матрица: 
 получили систему
получили систему 
 и
и 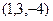 не коллинеарны, то прямые также и не параллельны. Таким образом, скрещивающиеся.
не коллинеарны, то прямые также и не параллельны. Таким образом, скрещивающиеся. .
. 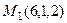 ,
,  . Вектор, соединяющий две прямых,
. Вектор, соединяющий две прямых,  .
. .
.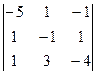 =
=  (прибавили 2-ю строку к 1-й)
(прибавили 2-ю строку к 1-й) =
=  , а по модулю получается 4.
, а по модулю получается 4. =
=  =
=  .
. =
= 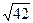 .
. =
= 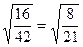 . Ответ.
. Ответ.  и
и  .
. .
. =
= 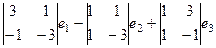 =
= 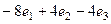 .
. коллинеарны,
коллинеарны,  . Значит, прямые параллельны или совпадают. Далее можно убедиться, что они не совпадающие. Возьмём точку
. Значит, прямые параллельны или совпадают. Далее можно убедиться, что они не совпадающие. Возьмём точку  , принадлежащую первой прямой (это получается при
, принадлежащую первой прямой (это получается при 
 и
и 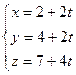 .
. . Возьмём точку (2,4,7), принадлежащую второй прямой, и подставим в эти уравнения.
. Возьмём точку (2,4,7), принадлежащую второй прямой, и подставим в эти уравнения. но первое не равно третьему, точка не лежит на первой прямой. Тогда прямые не совпадающие, а именно параллельны.
но первое не равно третьему, точка не лежит на первой прямой. Тогда прямые не совпадающие, а именно параллельны.  и
и  . Третий вектор, проведённый к какой-либо произвольной точке в этой плоскости, и 2 направляющих, образуют ЛЗС:
. Третий вектор, проведённый к какой-либо произвольной точке в этой плоскости, и 2 направляющих, образуют ЛЗС: 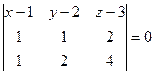

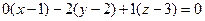
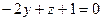
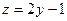 .
.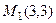 перпендикулярно вектору
перпендикулярно вектору 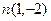 .
. параллельно вектору
параллельно вектору 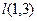 .
. и
и 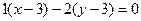
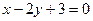 .
. и
и  , из чего следует
, из чего следует

 .
.

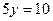 , откуда
, откуда 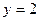 , тогда
, тогда 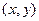 , которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим
, которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим 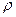 . Угол между осью
. Угол между осью  и этим отрезком обозначим
и этим отрезком обозначим  .
.
 это прилежащий катет, а
это прилежащий катет, а 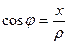 , аналогично
, аналогично  , откуда следуют такие формулы:
, откуда следуют такие формулы: 
 в полярных координатах.
в полярных координатах.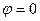 расстояние
расстояние  , при
, при  оно увеличивается до
оно увеличивается до 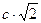 , а затем стремится к
, а затем стремится к 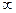 .
.
 . Получается
. Получается 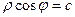 , тогда
, тогда  .
. получается
получается 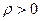 , и точка в правой полуплоскости. Но ведь косинус существует и не только в 4-й и 1-й четвертях, но и во 2-й и 3-й тоже. Но слева нет ни одной точки этой прямой. Нет ли в этом противоречия? На самом деле нет, потому что во 2 и 3 четвертях косинус отрицателен, а при
, и точка в правой полуплоскости. Но ведь косинус существует и не только в 4-й и 1-й четвертях, но и во 2-й и 3-й тоже. Но слева нет ни одной точки этой прямой. Нет ли в этом противоречия? На самом деле нет, потому что во 2 и 3 четвертях косинус отрицателен, а при 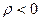 надо двигаться в обратную сторону по лучу, направленному влево, тем самым мы снова попадаем вправо, т.е. на ту же самую прямую, и фактически она прочерчивается второй раз.
надо двигаться в обратную сторону по лучу, направленному влево, тем самым мы снова попадаем вправо, т.е. на ту же самую прямую, и фактически она прочерчивается второй раз.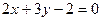 в полярных координатах.
в полярных координатах. , следовательно,
, следовательно, 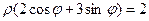 , откуда следует, что
, откуда следует, что  .
.  .
. с центром в точке
с центром в точке  радиуса
радиуса 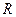 в полярных координатах.
в полярных координатах. 
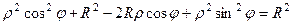

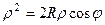
 . Чертёж:
. Чертёж: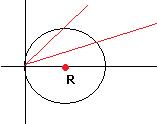
 в полярных координатах, сделать чертёж.
в полярных координатах, сделать чертёж.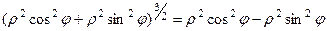
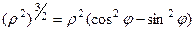

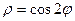 .
.


 в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ):
в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ):  . Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.
. Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.


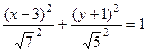 это каноническое уравнение.
это каноническое уравнение.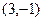 , полуоси
, полуоси  и
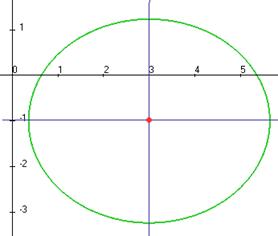
и 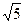 .
.

 , то есть надо сначала привести к главным осям квадратичную форму:
, то есть надо сначала привести к главным осям квадратичную форму:  . Строим её матрицу:
. Строим её матрицу: 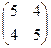 .
.
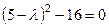
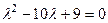
 .
. .
.  , оба уравнения пропорциональны, т.е. есть только такая информация:
, оба уравнения пропорциональны, т.е. есть только такая информация: 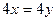 , т.е.
, т.е.  . ФСР: вектор (1,1).
. ФСР: вектор (1,1).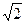 . Получаем
. Получаем - собственный вектор для
- собственный вектор для 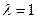 .
.  , оба уравнения пропорциональны, фактически оно одно:
, оба уравнения пропорциональны, фактически оно одно: 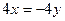 , т.е.
, т.е. 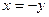 . ФСР: вектор
. ФСР: вектор 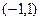 .
. собственный вектор для
собственный вектор для 
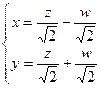
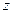 и
и 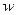 :
: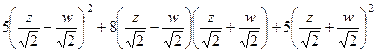



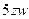 тоже сократятся.
тоже сократятся.
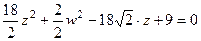
 .
.
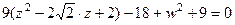
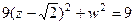
 , т.е.
, т.е. 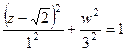 . Полуоси 1 и 3, то есть размеры эллипса: 2 на 6.
. Полуоси 1 и 3, то есть размеры эллипса: 2 на 6. , но это центр в новых координатах, а для чертежа надо найти центр именно в старых координатах
, но это центр в новых координатах, а для чертежа надо найти центр именно в старых координатах  .
.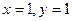 .
. , полуоси 1 и 3.
, полуоси 1 и 3.
 = const), и докажем, что в уравнении должна быть сумма квадратов.
= const), и докажем, что в уравнении должна быть сумма квадратов. и
и 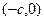 . Вычислим по теореме Пифагора расстояние от точки (x,y) до двух фокусов. F1 расположен дальше длина катета равна
. Вычислим по теореме Пифагора расстояние от точки (x,y) до двух фокусов. F1 расположен дальше длина катета равна  , тогда длина большего из двух отрезков, а именно
, тогда длина большего из двух отрезков, а именно 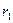 , равна:
, равна:  .
.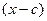 , тогда
, тогда  .
. , такая же сумма расстояний по определению должна быть и для произвольных точек. Итак,
, такая же сумма расстояний по определению должна быть и для произвольных точек. Итак, 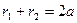 .
.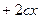 либо
либо 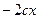 . Тогда можно так оценить разность квадратов:
. Тогда можно так оценить разность квадратов: =
=  =
=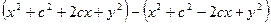 =
= 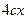 .
. , то есть
, то есть  .
.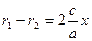 .
. :
: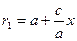 ,
, .
. . Теперь возведём в квадрат:
. Теперь возведём в квадрат: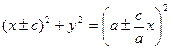 . Тогда
. Тогда  , далее
, далее  , тогда
, тогда 

 .
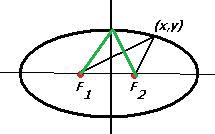
.  . Сумма расстояний до фокусов равна
. Сумма расстояний до фокусов равна  , то есть каждый отрезок, показанный зелёной линией на чертеже, имеет длину
, то есть каждый отрезок, показанный зелёной линией на чертеже, имеет длину  :
:
 ), а другой -
), а другой - 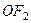 (длина равна
(длина равна  , тогда
, тогда  .
. .
.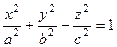 содержит прямолинейные образующие.
содержит прямолинейные образующие. 
 . Эта плоскость имеет уравнение
. Эта плоскость имеет уравнение  . Тогда в уравнении гиперболоида
. Тогда в уравнении гиперболоида 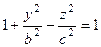 , т.е.
, т.е.  . Получается
. Получается  , т.е. в вертикальной плоскости две прямых:
, т.е. в вертикальной плоскости две прямых:  и
и  , или можно записать так:
, или можно записать так:  и
и  . Это пара пересекающихся прямых.
. Это пара пересекающихся прямых.
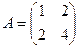 .
.

 ,
,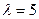 и
и  .
. 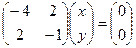 ,
,  уравнения пропорциональны, фактически это одно условие:
уравнения пропорциональны, фактически это одно условие:  . Собственным вектором является вектор
. Собственным вектором является вектор 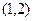 . Его модуль равен
. Его модуль равен 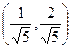 . Итак, получили первый вектор нового базиса.
. Итак, получили первый вектор нового базиса.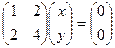 ,
,  уравнения пропорциональны. Фактически, это одно уравнение:
уравнения пропорциональны. Фактически, это одно уравнение:  . Вектор
. Вектор  . Нормируем и его тоже:
. Нормируем и его тоже:  .
. . Тогда:
. Тогда: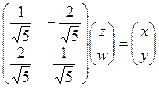
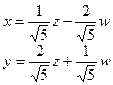
 +
+ = 0
= 0  +
+ = 0
= 0