
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продолжение 4: Факультативное.Содержание книги
Поиск на нашем сайте
Еще несколько практически значимых вопросов.
В вопросе о до-закупке сырья выяснилось, что твердо рекомендовать вложение денег в ослабление какого-то из ограничений (расширение бутылочного горлышка) можно только когда увеличение не превышает границ постоянства теневой цены. А что делать, если денег существенно больше? Как тогда выяснить оптимальное направление инвестиций?
В разборе кейса упоминалось, что в ходе оптимизации, при необходимости, можно получить и целочисленное решение проблемы (целочисленный план). Но с практической точки зрения интереснее не целое решение, а решение, кратное заданным числам, например величине упаковки или величине стандартной партии на производстве. Можно ли это сделать?
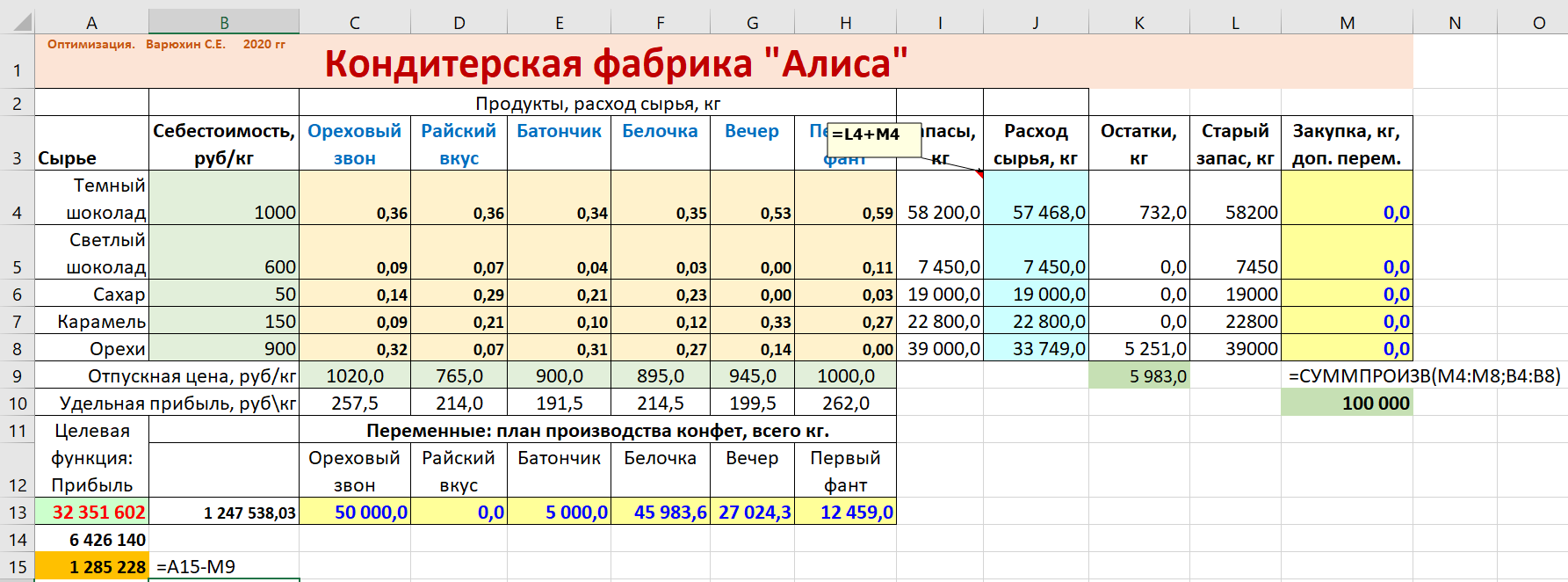
Мы отмечали, что при разных решениях остатки склада сильно варьируют. При том, что сырье дорогостоящее, может оказаться, что прибыль в каком-то решении меньше, но стоимость сырья гораздо выше. Не значит ли это, что стоимость сырья следует тоже учитывать и добавить ее к целевой функции, предположив, что сырье можно продать? Это наверняка изменило бы наши выводы о лучшем решении!
В сущности, проблему можно переформулировать так: сколько каждого вида сырья нужно закупить и сколько конфет разного вида произвести, чтобы максимизировать прибыль. В этом случае очевидно, что требуется добавить переменных в задачу. А именно, 5 переменных, по числу ресурсов, которые показывают, сколько каждого ресурса закупить. Ну и следует добавить закупленные ресурсы к запасам.
В столбец L скопируем изначальные запасы из I4:I8. В М4:М8 запланируем новые переменные.
В ячейках I4:I8 вместо фиксированных значений запишем формулу =L4+M4 и протянем до I8. Теперь запасы из ограничений задачи будут меняться с закупкой.
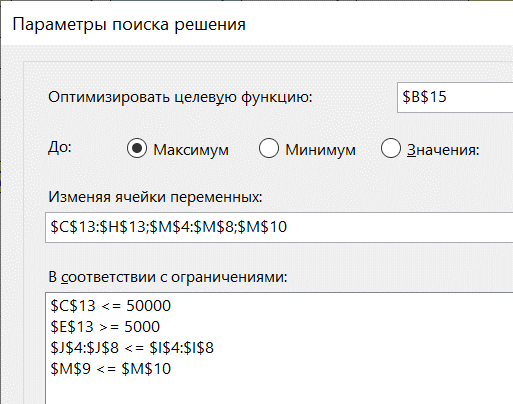
Ну и, учитывая канву задачи, пересчитаем бонус с учетом расходов на закупку M9: = A15-M9. Чтобы добавить в список переменных несвязанные диапазоны ячеек, уберем старые переменные, еще раз выделим C13:H13, зажмем кнопку CTRL и выделим M4:M8. Этот диапазон добавится через точку с запятой. Дополнительное ограничение, очевидно: M9<=M10. Все.
Теперь можно оптимизировать закупки при любых доступных суммах М10.
Правда, просто добавить ячейку М10 к переменным недостаточно. Раз мы желаем максимального бонуса, то в качестве ключевого KPI выберем именно ячейку B15 – бонус с учетом расходов. На листе ничего изменять не нужно.
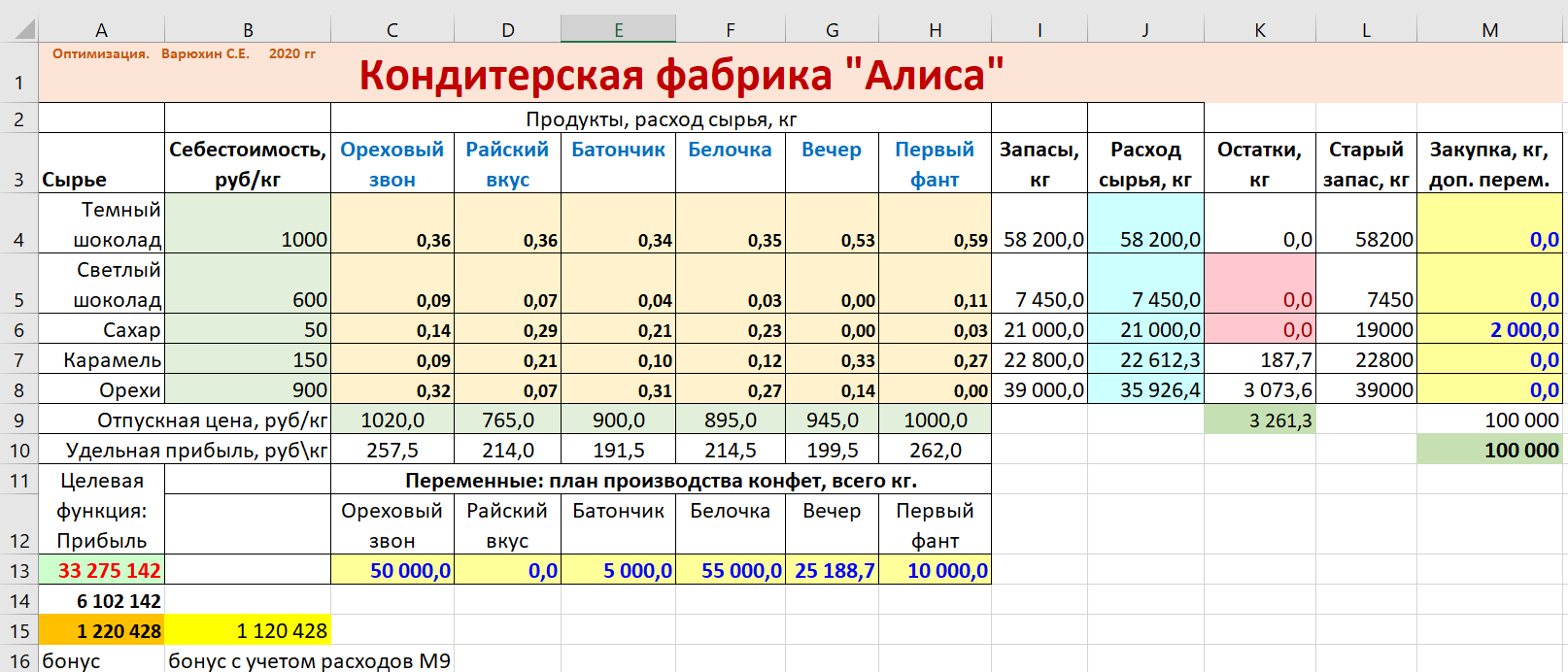
В результате получается, что максимальный бонус 1 166 282 руб достигается при инвестициях в закупку около 255 тыс.
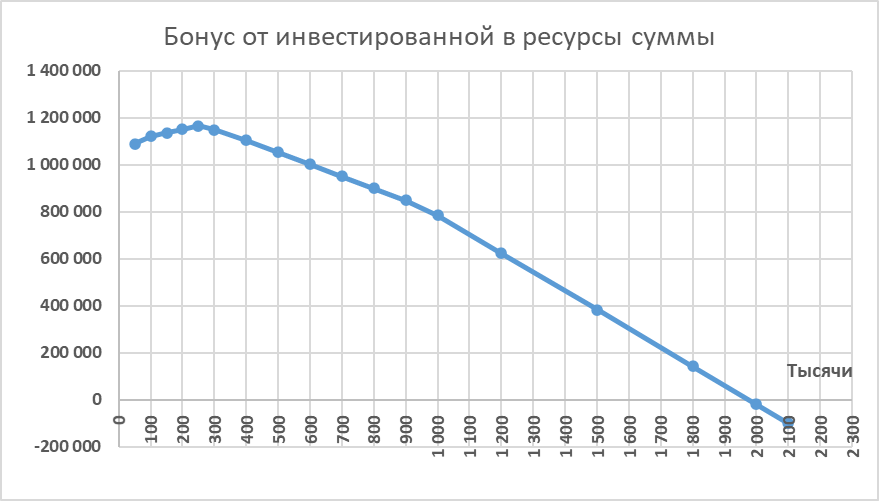
На графике, построенном по данным максимизации без переменной М10, это выглядит так.
Видно, что бонус сначала растет, а затем начинает уменьшаться. При инвестициях 2 млн руб бонус уходит в минус, кроме сахара закупается и светлый шоколад, но это уже мало интересно.
Идея поиска планов, кратных каким-то заданным значениям, проста: давайте в качестве переменных выберем количество упаковок и именно его сделаем целым. Опыт проведем на базовом решении с ограничениями только на ресурсы, сделав копию страницы.
После этого введем новые переменные в строке 17 и запишем туда какой-нибудь вариант плана. Например, всех конфет по 100 упаковок.
После этого вместо старых переменных C13:H13 запишем формулы вида: =С15*С17, чтобы в этих ячейках по-прежнему фигурировали количества продукции в кг и остальные формулы не пришлось корректировать.
Осталось вызвать «Поиск решения» и заменить переменные на С17:H17, а также добавить целочисленные ограничения С17:H17=целые.
Решение не будет сильно отличаться от исходного, но план станет кратным заданным в 15-й строке числам.
На самом деле попытка приплюсовать к прибыли деньги от продажи остатков сырья - заблуждение. Потому что прибыль вычисляется как выручка минус расходы. И для неиспользованного сырья, которое не с неба упало, должно быть так же. И тут уж очевидно, что продажа сырья в реальных условиях принесет скорее убыток и прибыль уменьшится (кроме особой ситуации, когда мы купили сырье, а цены на него взлетели). Но все-таки, можно ли как-то учесть стоимость остатков сырья?
Можно. Но тогда нужно менять целевую функцию. Потому что полную стоимость сырья имеет смысл сопоставлять только с выручкой. Выручка в данной ситуации может быть и более разумным целевым показателем, поскольку деньги на закупку ресурсов уже потрачены и максимизация прибыли – это максимизация чисто формального показателя. В то время как выручка как раз показывает, сколько денег мы можем извлечь из уже имеющихся ресурсов.
Подсчитать выручку не сложно, нужно план перемножить не на прибыль, а на отпускные цены (B13) =СУММПРОИЗВ(C9:H9;C13:H13).
Если теперь в качестве целевой ячейки выбрать B13 и выполнить оптимизацию, выручка подрастет, а прибыль уменьшится. Правда, незначительно.
И вот к этой выручке можно теперь добавить стоимость сырья. Сосчитаем в K11 стоимость сырья =СУММПРОИЗВ(K4:K8;B4:B8), а в K13 сумму выручки и стоимость сырья =K11+B13.
Теперь можно выбрать в качестве целевой ячейки K13 и учесть явным образом стоимость остатков сырья. Но результат оптимизации получается довольно интересный.
А именно: точно такой же, как при максимизации прибыли. Ожидаемо, если задуматься, правда?
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.159 (0.007 с.) |


 Чтобы закупка не оказалась бесконечно большой, подсчитаем стоимость закупленного сырья в М9, а в М10 запишем предельную сумму, например 100 тыс.
Чтобы закупка не оказалась бесконечно большой, подсчитаем стоимость закупленного сырья в М9, а в М10 запишем предельную сумму, например 100 тыс.
 Причем, как несложно убедиться буквально с нескольких попыток, бонус при инвестициях в районе 1 млн руб. оказывается явно меньше, чем при инвестициях 50-100 тыс. Это наталкивает на идею поварьировать в качестве переменной и максимальную сумму инвестиций в ресурсы M10!
Причем, как несложно убедиться буквально с нескольких попыток, бонус при инвестициях в районе 1 млн руб. оказывается явно меньше, чем при инвестициях 50-100 тыс. Это наталкивает на идею поварьировать в качестве переменной и максимальную сумму инвестиций в ресурсы M10!

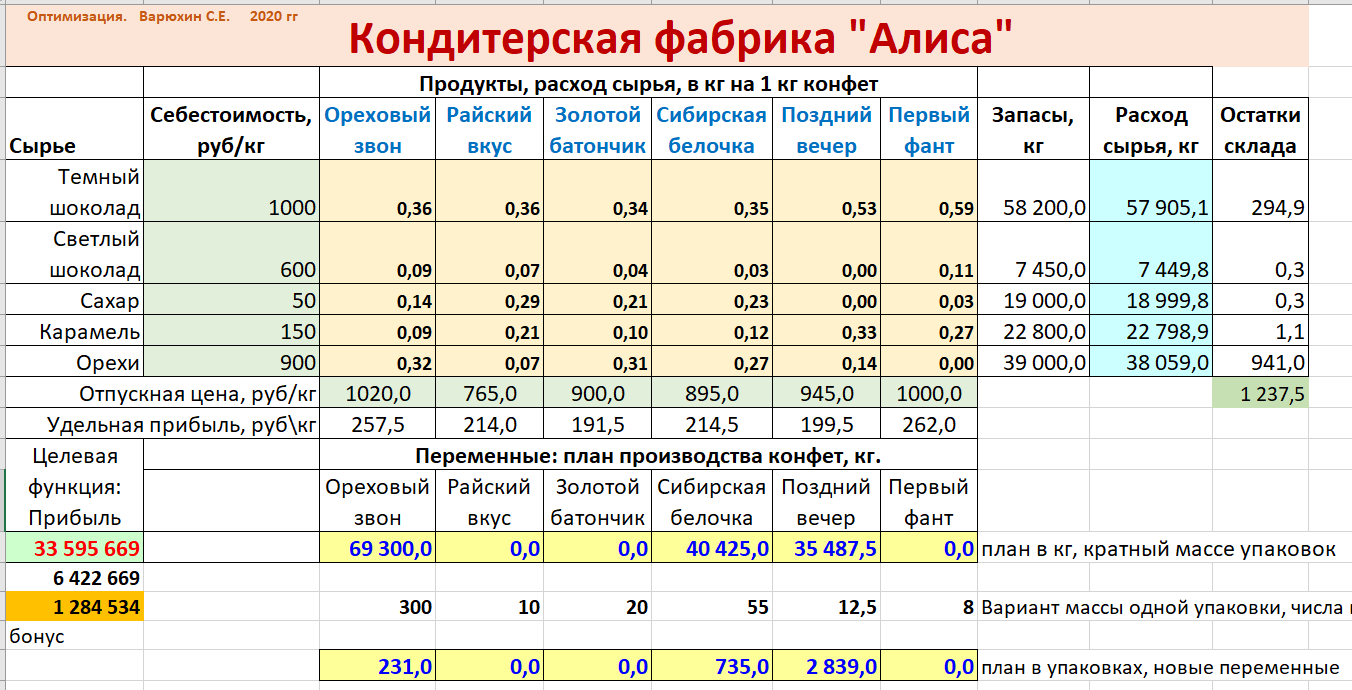 В строке 15 зададим размер упаковок в килограммах. Вес упаковок задан произвольно, но так, чтобы были сильно отличающиеся варианты.
В строке 15 зададим размер упаковок в килограммах. Вес упаковок задан произвольно, но так, чтобы были сильно отличающиеся варианты.






