
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление случайных погрешностейСодержание книги
Поиск на нашем сайте Для удобства анализа предположим, что систематическая погрешность равна 0. В этом случае абсолютная погрешность будет только случайной. Случайная погрешность измерений описывается и оценивается с помощью теории вероятности и математической статистики. Основной характеристикой случайной погрешности является вероятность нахождения погрешности результата измерения в заданном интервале, имеющем нижнюю и верхнюю границу. Для определения значения вероятности необходимо знать закон распределения случайной погрешности, который описывается плотностью вероятности или функцией распределения. Закон распределения случайной погрешности представляется в виде плотности распределения вероятностей f (D) или функцией распределения вероятностей F (D), которые связаны следующим соотношением:
Значение функции распределения представляет собой вероятность того, что погрешность не превысит заданного граничного значения
Функция распределения обладает следующим свойствами: 1) 2) 3) возрастание при возрастании Вероятность попадания погрешности в заданный интервал определяется выражением
Очевидно, что вероятность попадания погрешности в бесконечно большой интервал равна единице. Для описания случайной погрешности часто используется такая числовая характеристика, как дисперсия:
Дисперсия характеризует разброс погрешностей относительно ожидаемого значения 0. Поскольку дисперсия имеет квадратичную размерность, вместо нее используют среднеквадратичное отклонение (СКО) В практике измерений наиболее часто используются: – нормальный закон; – равномерный; – треугольный; – Стьюдента. Нормальный закон распределения
СКО характеризует точность измерений (при ее увеличении «горб» ниже, «хвосты» длиннее). Закон может быть использован при следующих допущениях: – погрешность является непрерывной величиной на бесконечно большом интервале; – при выполнении большого числа измерений большие погрешности появляются реже, чем малые; – частота появления равных по величине, но противоположных по знаку погрешностей, одинакова; – результаты наблюдений формируются под влиянием большого числа факторов, каждый из которых оказывает незначительное влияние по сравнению с суммой всех остальных (центральная предельная теорема); – число наблюдений более 20. Вероятность попадания погрешности в симметричный интервал от
Для удобства использования справочников и математических программных пакетов переменную D заменяют на безразмерную t = D/s. Граница интервала погрешностей выражается величиной При использовании безразмерных величин вероятность попадания погрешности в интервал на основании нормального закона распределения принимает вид
Функция Для определения вероятности попадания погрешности в заданный интервал и, наоборот, определения интервала, в который погрешность попадает с заданной вероятностью, удобно использовать интервалы, выраженные через s. Ниже приведена таблица соответствия между границами интервалов и вероятностями попадания в них погрешности. Таблица 3.1 Вероятности попадания погрешности в интервал
Закон распределения Стьюдента Закон применяется, когда случайные погрешности распределены по нормальному закону и число измерений от 3 до 20. Закон описывает распределение плотности вероятности значений случайной величины:
Он отличается от нормального закона тем, что: – учитывает число наблюдений n; – s является СКО среднего арифметического. Особенности распределения Стьюдента: – при n < 3 становится бесконечным СКО; – классический аппарат математической статистики не работает, и для анализа необходимо использовать доверительные оценки. Распределение Стьюдента мало отличается от нормального при При n < 20 для поиска вероятности попадания величины t в интервал (
Величину Равномерный закон распределения
Равномерный закон применяется при следующем допущении: случайная погрешность принимает любые значения в ограниченном интервале ( Вероятность нахождения погрешности в интервале (
Области применения равномерного закона для описания случайных погрешностей: – метод дискретного счета для измерения непрерывной величины; – аналого-цифровое преобразование; – отсчет показаний со шкалы прибора.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

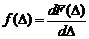 .
.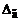 :
: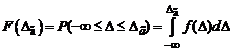 .
.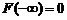 ;
; ;
; .
.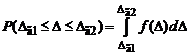 .
.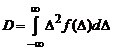 .
.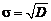 .
.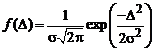 .
.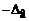 до
до 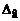 :
: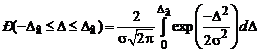 .
. .
.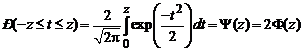 .
.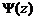 является интегралом вероятностей, которая выражает вероятность попадания случайной величины в интервал от – z
является интегралом вероятностей, которая выражает вероятность попадания случайной величины в интервал от – z  выражает вероятность попадания случайной величины в интервал от 0 до + z. Ее называют интегралом вероятностей или функцией Лапласа.
выражает вероятность попадания случайной величины в интервал от 0 до + z. Ее называют интегралом вероятностей или функцией Лапласа.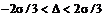
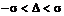
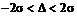

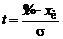 ,
, 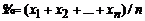 .
.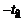 ,
,  ) используют уравнение
) используют уравнение .
. называют коэффициентом Стьюдента. При расчете погрешностей измерений задают допустимую вероятность и число наблюдений и находят
называют коэффициентом Стьюдента. При расчете погрешностей измерений задают допустимую вероятность и число наблюдений и находят  .
.
 ;
; 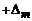 ).
).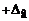 ):
): .
.


