
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Г. Базы данных, информационно-справочные и поисковые системыСодержание книги
Поиск на нашем сайте
Автоматизированная информационно-библиотечная система «Марк». ЭБС IPRbooks: www.iprbookshop.ru. ЭБС ВСЭИ:http://edu/vs_library/index.php Приложения Приложение 1
Приложение к заданию № 3
Линейные дифференциальные уравнения http://kurs.ido.tpu.ru/courses/tay/chapter_2/glv_2_page_1.html
Наиболее общей и наиболее полной формой математического описания автоматических систем и их элементов является дифференциальное уравнение вида. Желаемый закон в них имеет вид
где Уравнение (1) устанавливает связь между входной и выходной величиной как в переходных, так и в установившихся режимах. Коэффициенты дифференциального уравнения называются параметрами. Они зависят от различных физических констант, характеризующих скорость протекания процессов в элементах. Такими константами являются, например, массы движущихся частей, индуктивности и емкости электрических цепей, теплоемкости нагреваемых элементов. Иногда параметры некоторых элементов систем изменяются во времени. Такую систему называют нестационарной или системой с переменными параметрами. Системой с переменными параметрами является, например, автоматическая система управления приводом поворота мощного экскаватора, если в процессе его поворота одновременно происходит выдвижения рукояти с ковшом. В большинстве практических случаев коэффициенты уравнения существенно не изменяются и системы являются системами с постоянными параметрами. В дальнейшем будут рассматриваться только такие системы. Для автоматических систем управления, описываемых линейным уравнением, справедлив принцип наложения или суперпозиции, согласно которому изменение выходной величины Это свойство линейных систем имеет большое практическое значение, так как благодаря ему значительно облегчаются все расчеты. Рассмотрим типовые формы записи линейного дифференциального уравнения (1), используемые в различных задачах теории автоматического управления. Все физические переменные, входящие в уравнение, могут быть выражены в относительных единицах. Для этого каждое слагаемое делят на постоянную величину, имеющую размерность той переменной, которая входит в это слагаемое. Постоянные величины называют базовыми. В качестве базовых величин обычно принимают номинальные или установившиеся значения переменных
Удобной формой записи линейных дифференциальных уравнений является символическая или операторная. Переход к операторной форме осуществляют введением сокращенного условного обозначения операции дифференцирования:
тогда уравнение (2) в символической форме будет иметь вид.
Многочлены от
называют собственным оператором, а многочлен
называют входным оператором или оператором воздействия. Название "собственный оператор" обусловлено тем, что многочлен У всех реальных элементов и систем порядок наивысшей производной во входном операторе не может быть больше порядка наивысшей производной в собственном операторе, т.е. всегда Уравнения элементов невысокого порядка
путем деления всех членов на коэффициент
где Коэффициенты
Пример 1 Составить дифференциальное уравнение электрической цепи (рис. 1).
Рисунок 1. Схема одноконтурной электрической цепи Решение. Входной величиной для цепи является напряжение
Выходное напряжение
откуда определим значение тока
Подставим (10) в (8):
Уравнение (11) является интегро-дифференциальным и его необходимо привести к дифференциальной форме. После дифференцирования (11) получим:
Уравнение (12) приводится к стандартной форме:
где В операторной форме уравнение (13) представляется как
Временные характеристики Дифференциальное уравнение является самой общей формой описания элемента и не дает наглядного представления о передаточных свойствах элемента. Наглядное представление об этих свойствах дает функция Наиболее наглядное представление о динамических свойствах элемента дает его переходная функция (характеристика). Переходной функцией Переходная функция
Свободная составляющая может быть найдена как решение однородного дифференциального уравнения (при отсутствии одинаковых корней):
где
Рисунок 2. Переходная (а) и импульсная (б) характеристики Переходная функция определится как сумма вынужденной и свободной составляющих. Характеристическое уравнение, соответствующее определенному дифференциальному уравнению, представляет собой алгебраическое уравнение, степень и коэффициенты которого совпадают с порядком и коэффициентами левой части этого уравнения. Для дифференциального уравнения, записанного в форме (6), характеристическое уравнение имеет вид
Структура характеристического уравнения (2.10) совпадает со структурой левой части уравнения (2.3) и со структурой собственного оператора
Для линейных элементов и систем, кроме принципа суперпозиции, справедливо еще одно общее правило: реакция Импульсной переходной функцией Импульсная переходная функция
и наоборот, переходная функция равна интегралу от импульсной переходной функции:
Переходные характеристики называют также временными. Пример 2 Для электрической цепи (рис. 3) определить переходную функцию.
Рисунок 3. Электрическая RC-цепь и ее переходная функция Решение. Электрической цепи соответствуют уравнения:
которые путем исключения промежуточной переменной
или в стандартной форме:
где Из (22) составляем характеристическое уравнение
и определяем корень Переходная функция
При Окончательно имеем
Переходная функция показана на рис. 3.
|
|||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.49.94 (0.008 с.) |

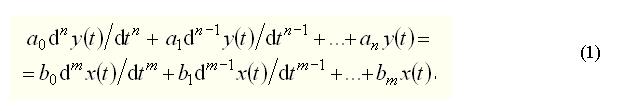
 и
и  – входная и выходная величины элемента или системы;
– входная и выходная величины элемента или системы;  – коэффициенты уравнения.
– коэффициенты уравнения.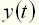 , возникающее при действии на систему нескольких входных сигналов
, возникающее при действии на систему нескольких входных сигналов 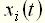 , равно сумме изменений
, равно сумме изменений 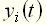 величины
величины 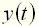 , вызываемых каждым сигналом в отдельности.
, вызываемых каждым сигналом в отдельности.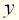 и
и 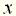 .
.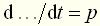 . Соответственно, k-ю производную переменной
. Соответственно, k-ю производную переменной 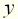 обозначают,
обозначают, 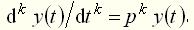 (2)
(2)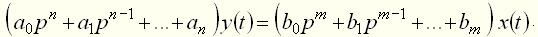 (3)
(3)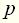 степени
степени 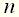 и
и 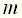 , находящиеся в левой и правой частях уравнения (3), называются дифференциальными операторами. Каждый такой оператор устанавливает соответствие между функцией времени и определенной совокупностью производных этой функции. Многочлен
, находящиеся в левой и правой частях уравнения (3), называются дифференциальными операторами. Каждый такой оператор устанавливает соответствие между функцией времени и определенной совокупностью производных этой функции. Многочлен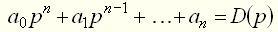 (4)
(4)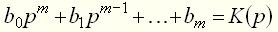 (5)
(5)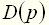 характеризует собственное (свободное) движение элемента, т.е. движение при отсутствии внешних воздействий. Оператор
характеризует собственное (свободное) движение элемента, т.е. движение при отсутствии внешних воздействий. Оператор 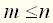 . Если это условие не выполняется, то уравнение соответствует физически нереализуемой системе.
. Если это условие не выполняется, то уравнение соответствует физически нереализуемой системе.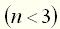 в теории автоматического управления принято записывать в так называемой стандартной форме. При стандартной форме записи уравнение преобразовывают таким образом, чтобы коэффициент при выходной величине был равен единице. При этом коэффициент перед входной величиной в правой части уравнения становится равным передаточному коэффициенту, а коэффициенты при производных выходной величины будут иметь размерность времени в степени, равной порядку соответствующей производной. Например, уравнение второго порядка
в теории автоматического управления принято записывать в так называемой стандартной форме. При стандартной форме записи уравнение преобразовывают таким образом, чтобы коэффициент при выходной величине был равен единице. При этом коэффициент перед входной величиной в правой части уравнения становится равным передаточному коэффициенту, а коэффициенты при производных выходной величины будут иметь размерность времени в степени, равной порядку соответствующей производной. Например, уравнение второго порядка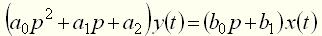 (6)
(6)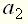 может быть приведено к стандартной форме
может быть приведено к стандартной форме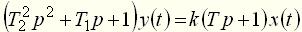 , (7)
, (7)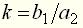 ,
, 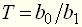 ,
, 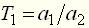 ,
, 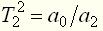 .
.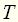 ,
, 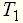 ,
, 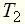 , принято называть постоянными времени, характеризующими динамические свойства элемента.
, принято называть постоянными времени, характеризующими динамические свойства элемента.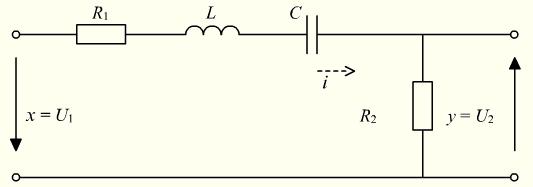
 , а выходной величиной – напряжение
, а выходной величиной – напряжение  . В динамических режимах по одноконтурной цепи протекает ток
. В динамических режимах по одноконтурной цепи протекает ток  . Выходное напряжение равно падению напряжения на сопротивлении
. Выходное напряжение равно падению напряжения на сопротивлении 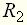 . На основании второго закона Кирхгофа при нулевых начальных условиях составим уравнение:
. На основании второго закона Кирхгофа при нулевых начальных условиях составим уравнение: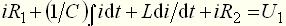 . (8)
. (8)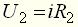 , (9)
, (9)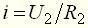 . (10)
. (10)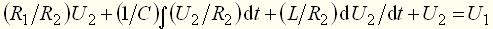 . (11)
. (11)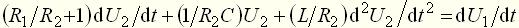 (12)
(12)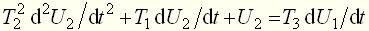 (13)
(13)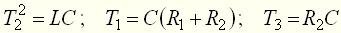 .
.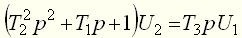 . (14)
. (14) , являющаяся решением дифференциального уравнения. Но одно и то же дифференциальное уравнение может иметь множество решений, зависящих от начальных условий и вида внешнего воздействия
, являющаяся решением дифференциального уравнения. Но одно и то же дифференциальное уравнение может иметь множество решений, зависящих от начальных условий и вида внешнего воздействия  . Поэтому принято динамические свойства элементов и систем характеризовать решением, соответствующим нулевым начальным условиям и одному из типовых воздействий. В качестве типового воздействия принимают единичное ступенчатое, дельта-функцию или гармоническое воздействие.
. Поэтому принято динамические свойства элементов и систем характеризовать решением, соответствующим нулевым начальным условиям и одному из типовых воздействий. В качестве типового воздействия принимают единичное ступенчатое, дельта-функцию или гармоническое воздействие. . называют изменение выходной величины
. называют изменение выходной величины 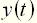 во времени, возникающее после подачи на вход единичного ступенчатого воздействия, при нулевых начальных условиях. Переходная функция может быть задана в виде графика (рис. 2, а) или аналитически.
во времени, возникающее после подачи на вход единичного ступенчатого воздействия, при нулевых начальных условиях. Переходная функция может быть задана в виде графика (рис. 2, а) или аналитически.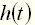 , как и любое решение неоднородного дифференциального уравнения, имеет две составляющие: вынужденную
, как и любое решение неоднородного дифференциального уравнения, имеет две составляющие: вынужденную 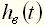 и свободную
и свободную 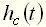 . Вынужденная составляющая переходного процесса представляет собой частное решение исходного уравнения. При ступенчатом воздействии вынужденная составляющая равна установившемуся значению выходной величины, которое для статических элементов может быть определено непосредственно из дифференциального уравнения (при нулевых производных):
. Вынужденная составляющая переходного процесса представляет собой частное решение исходного уравнения. При ступенчатом воздействии вынужденная составляющая равна установившемуся значению выходной величины, которое для статических элементов может быть определено непосредственно из дифференциального уравнения (при нулевых производных):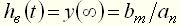 . (15)
. (15)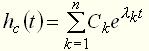 , (16)
, (16)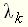 – корни характеристического уравнения;
– корни характеристического уравнения; 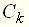 – постоянные интегрирования, зависящие от начальных условий.
– постоянные интегрирования, зависящие от начальных условий.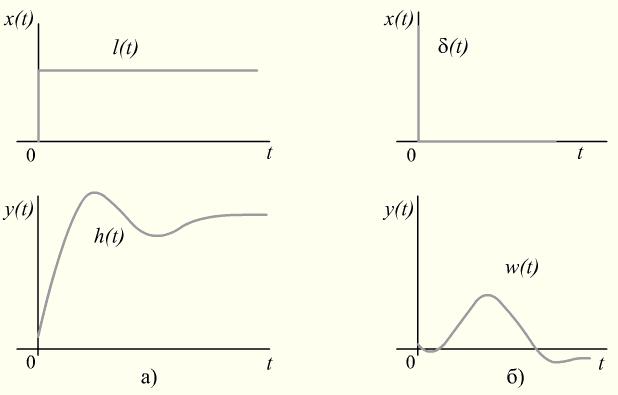
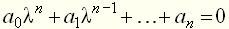 . (17)
. (17)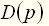 (см. (4)). Поэтому при записи характеристического уравнения часто вместо символа
(см. (4)). Поэтому при записи характеристического уравнения часто вместо символа 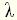 , обозначающего неизвестную переменную алгебраического уравнения, используют символ
, обозначающего неизвестную переменную алгебраического уравнения, используют символ 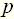 . Но при этом
. Но при этом 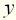 на неединичное воздействие
на неединичное воздействие 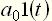 равна
равна 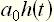 .
.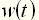 называют изменение выходной величины
называют изменение выходной величины 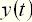 , возникающее после подачи на вход дельта-функции, при нулевых начальных условиях (рис. 2, б).
, возникающее после подачи на вход дельта-функции, при нулевых начальных условиях (рис. 2, б).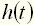 :
: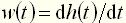 , (18)
, (18)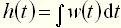 . (19)
. (19)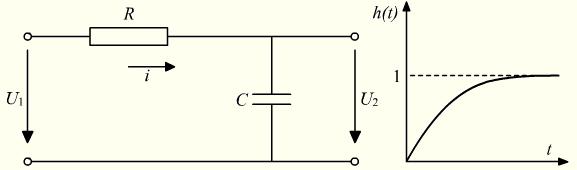
 (20)
(20) приводятся к одному дифференциальному уравнению:
приводятся к одному дифференциальному уравнению: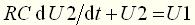 (21)
(21)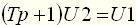 , (22)
, (22)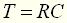 .
.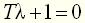 (23)
(23)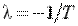 .
.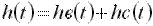 . При единичном воздействии
. При единичном воздействии 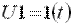 вынужденная составляющая также равна единице:
вынужденная составляющая также равна единице: 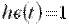 . Тогда
. Тогда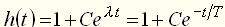 (24)
(24)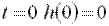 , и тогда из (24) определим постоянную интегрирования
, и тогда из (24) определим постоянную интегрирования 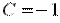 .
.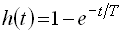 (25)
(25)


