
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операционный метод и передаточная функцияСодержание книги Поиск на нашем сайте Наиболее распространенным методом описания и анализа автоматических систем является операционный метод. В основе метода лежит преобразование Лапласа:
которое устанавливает соответствие между функциями действительной переменной Преобразование Лапласа выполнимо лишь для таких функций времени, которые равны нулю при Наиболее важными свойствами преобразования Лапласа являются свойства, формулируемые обычно в виде правил: при нулевых начальных условиях дифференцированию оригинала Именно на этих двух свойствах основан операционный метод решения дифференциальных уравнений, который заключается в следующем. Исходное дифференциальное (или интегро-дифференциальное) уравнение, записанное относительно искомой выходной функции Широкое распространение операционного метода в теории автоматического управления обусловлено тем, что с его помощью определяют так называемую передаточную функцию, которая является самой компактной формой описания динамических свойств элементов и систем. Применим преобразование Лапласа к линейному дифференциальному уравнению (1), полагая, что до приложения внешнего воздействия система находилась в покое и все начальные условия равны нулю. Используя свойство линейности и правило дифференцирования, можно получить алгебраическое уравнение в изображениях:
где
Сравнивая уравнение (27) с уравнением в символической форме (3), можно заметить полную аналогию их структур. Различие уравнений лишь в значении символа Введем понятие передаточной функции. Передаточной функцией
Для системы, описываемой уравнением (1), передаточная функция равна отношению входного оператора
Как следует из (28) и (29), передаточная функция представляет собой некоторый динамический оператор, характеризующий прохождение сигналов через линейный элемент. Рассмотрим основные свойства и особенности передаточных функций автоматических систем и их элементов. Передаточная функция элемента связана с его импульсной переходной функцией преобразованием Лапласа:
Для реальных элементов, описываемых обыкновенными дифференциальными уравнениями, передаточная функция представляет собой правильную рациональную дробь, у которой степень многочлена числителя меньше или равна степени многочлена знаменателя, т. е. Передаточная функция является функцией комплексной переменной
где
По распределению нулей и полюсов передаточной функции на комплексной плоскости с координатами Пример 3 Найти передаточную функцию для электрической цепи, схема которой приведена в примере 1 (рис. 1). Входной величиной является напряжение Передаточную функцию электрических цепей удобно получить на основе операторной схемы замещения цепи для нулевых начальных условий. Напомним, что операторное сопротивление индуктивности равно
Рисунок 4. Операторная схема замещения для определения W(p) Решение. Для операторной схемы замещения относительно изображений переменных справедливы законы Кирхгофа. На основании 2-го закона Кирхгофа составим уравнение
Изображение выходного напряжения с изображением тока связано соотношением
Исключив из уравнений промежуточную величину
откуда определим передаточную функцию как
Значения постоянных времени Тот же результат может быть получен и из уравнения (7) примера 1. Пример 4 Найти аналитические выражения для частотных характеристик для цепи (пример 3, рис. 4), имеющей передаточную функцию
Решение. Амплитудно-фазовая функция цепи равна (замена
Выражение для амплитудной частотной характеристики найдем как
Фазовая частотная характеристика определится как разность аргументов числителя и знаменателя
Приложение 2
Приложение к заданию № 4
|
||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.204 (0.008 с.) |

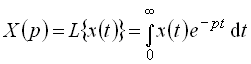 , (26)
, (26)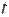 и функциями комплексной переменной
и функциями комплексной переменной 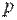 . Функцию времени
. Функцию времени 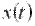 , входящую в интеграл Лапласа, называют оригиналом, а результат интегрирования – функцию
, входящую в интеграл Лапласа, называют оригиналом, а результат интегрирования – функцию 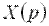 – изображением функции
– изображением функции  . Это условие обеспечивается обычно умножением функции
. Это условие обеспечивается обычно умножением функции  . С математической и физической точек зрения такой искусственный прием вполне корректен, так как функции
. С математической и физической точек зрения такой искусственный прием вполне корректен, так как функции 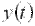 , заменяют на алгебраическое уравнение относительно изображения
, заменяют на алгебраическое уравнение относительно изображения 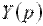 (это называется алгебраизацией дифференциального уравнения), затем, решая алгебраическое уравнение при заданном
(это называется алгебраизацией дифференциального уравнения), затем, решая алгебраическое уравнение при заданном 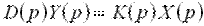 (27)
(27)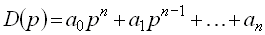 ,
,
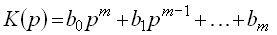 .
.
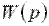 : называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях:
: называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях: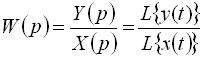 . (28)
. (28)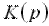 к собственному оператору
к собственному оператору 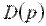 :
: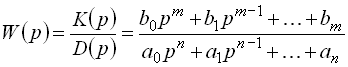 . (29)
. (29) 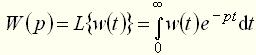 . (30)
. (30)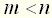 . Все коэффициенты передаточной функции – действительные числа, характеризующие параметры элемента.
. Все коэффициенты передаточной функции – действительные числа, характеризующие параметры элемента.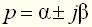 , которая может при некоторых значениях переменной
, которая может при некоторых значениях переменной 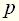 обращаться в нуль или бесконечность. Значение переменной
обращаться в нуль или бесконечность. Значение переменной 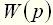 обращается в нуль, называют нулем, а значение, при котором обращается в бесконечность, – полюсом передаточной функции. Очевидно, что нулями передаточной функции являются корни полинома
обращается в нуль, называют нулем, а значение, при котором обращается в бесконечность, – полюсом передаточной функции. Очевидно, что нулями передаточной функции являются корни полинома 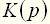 , а полюсами - корни полинома
, а полюсами - корни полинома 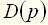 . Корни полиномов числителя и знаменателя могут быть комплексными, мнимыми и вещественными числами (в том числе и нулевыми). Если эти корни известны, то передаточная функция может быть представлена в следующем виде:
. Корни полиномов числителя и знаменателя могут быть комплексными, мнимыми и вещественными числами (в том числе и нулевыми). Если эти корни известны, то передаточная функция может быть представлена в следующем виде: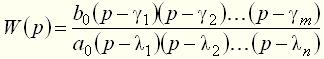 , (31)
, (31)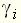 – корни многочлена
– корни многочлена 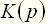 (нули
(нули 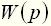 );
); 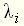 – корни многочлена
– корни многочлена 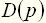 (полюсы
(полюсы 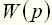 ).
).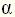 и
и 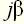 можно судить о свойствах элемента или системы.
можно судить о свойствах элемента или системы.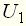 , а выходной – напряжение
, а выходной – напряжение 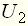 .
.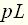 , емкости –
, емкости – 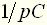 , а активного сопротивления –
, а активного сопротивления – 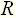 . На рис. 4 приведена операторная схема замещения рассматриваемой цепи.
. На рис. 4 приведена операторная схема замещения рассматриваемой цепи.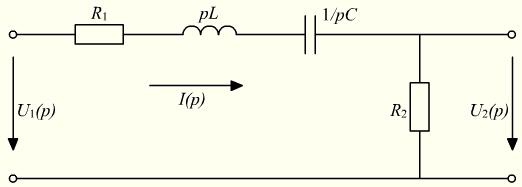
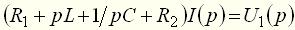 . (32)
. (32)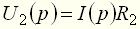 . (33)
. (33)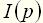 , после преобразований получим
, после преобразований получим 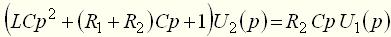 , (34)
, (34)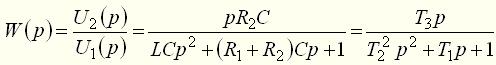 . (35)
. (35)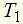 ,
, 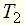 и
и 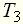 приведены в примере 1.
приведены в примере 1.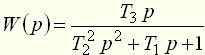 .
. 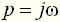 )
)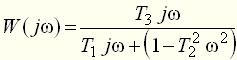 .
.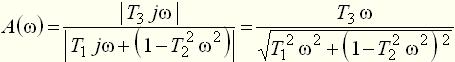 .
.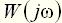 :
: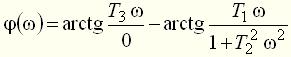 .
. 


