Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальные тесты проверки точности моделирования БСВСодержание книги
Поиск на нашем сайте Поскольку БСВ используются при моделировании всех других случайных элементов, точность моделирования для датчиков БСВ должна проверяться особенно тщательно. В терминах статистической проверки гипотез данная задача формулируется следующим образом. По выборке значений
Для этой цели наряду с традиционными статистическими критериями проверки точности моделирования СВ (критериями согласия, критериями серий и др.), применяется ряд специальных тестов. В пакете СТАТМОД реализованы следующие тесты данной группы:
· тест «совпадения моментов»;
· тест «ковариация»;
· тест «равномерность двумерного распределения».
Тест «совпадения моментов»
Пусть в результате
-- случайные отклонения выборочных оценок
от истинных характеристик Тест «совпадения моментов» -- это программа для ЭВМ, реализующая статистические критерии проверки по выборке А гипотез:
Решающее правило для проверки гипотез (4), (5) имеет вид:
принимается
где: Если
находится выражение для порога критериев:
Δ = Ф-1(1 -
где Ф-1 В пакете СТАТМОД предполагается эквивалентной формы решающих правил (6), связывающей задаваемый пользователем уровень значимости
принимается где
Тест «ковариация»
Ковариационной функцией случайной последовательности
Если
Пусть
где 1<t<< Тест «ковариация» позволяет проверить свойство (7) (гипотезу
принимается
где:
Δ = Ф-1(1 -
В пакете СТАТМОД предполагается использование эквивалентной формы правила (8):
принимается
где
Представим (8) в виде: принимается Здесь Решающее правило в форме (9) удобно использовать при визуальном анализе графиков ковариационной функции
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

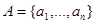 , полученной в результате
, полученной в результате 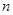 - кратного обращения к датчику БСВ необходимо проверить гипотезу
- кратного обращения к датчику БСВ необходимо проверить гипотезу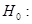 выборочные значения
выборочные значения 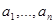 являются реализациями независимых СВ
являются реализациями независимых СВ  , равномерно распределённых на [0,1); конкурирующая гипотеза
, равномерно распределённых на [0,1); конкурирующая гипотеза 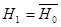 .
.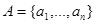 . Известно, что БСВ имеет среднее значение
. Известно, что БСВ имеет среднее значение  и дисперсию
и дисперсию  . Обозначим:
. Обозначим: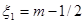 ,
, 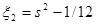
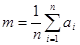 ,
, 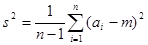
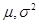 .
.
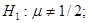 (4)
(4) ,
,  (5)
(5)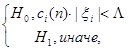 (6)
(6)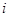 ={1 — для соотношений (4); 2 – для соотношений (5)};
={1 — для соотношений (4); 2 – для соотношений (5)}; 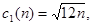
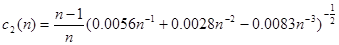 -- нормировочные множители; ∆ -- порог критерия.
-- нормировочные множители; ∆ -- порог критерия.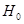 верна, а
верна, а 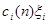 ~Ν1(0,1) (распределено приближённо по стандартному нормальному закону). С учётом этого из ограничения на вероятность ошибки первого рода:
~Ν1(0,1) (распределено приближённо по стандартному нормальному закону). С учётом этого из ограничения на вероятность ошибки первого рода: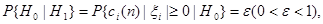
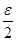 ),
), -- квантиль стандартного нормального закона,
-- квантиль стандартного нормального закона, 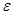 -- заданный уровень значимости.
-- заданный уровень значимости.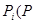 -значения):
-значения):

 называется функция целочисленной переменной
называется функция целочисленной переменной  :
: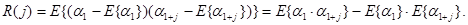
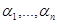 -- независимые, одинаково распределённые по закону R(0,1) случайные величины, то
-- независимые, одинаково распределённые по закону R(0,1) случайные величины, то 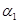 и
и 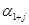 независимы для любого
независимы для любого  и следовательно:
и следовательно: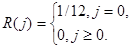 (7)
(7) -- оценка
-- оценка 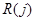 по выборке
по выборке 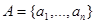 , полученной в результате
, полученной в результате 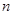 - кратного обращения к исследуемому датчику:
- кратного обращения к исследуемому датчику:
 -- выборочное среднее. Заметим, что
-- выборочное среднее. Заметим, что 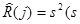 - выборочная дисперсия).
- выборочная дисперсия). ) для последовательности
) для последовательности 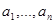 и описывается следующим решающим правилом:
и описывается следующим решающим правилом: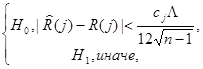 (8)
(8)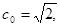
 для
для  Δ - порог, определённый для заданного уровня значимости
Δ - порог, определённый для заданного уровня значимости  по формуле:
по формуле: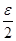 ).
).
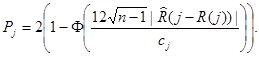
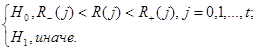 (9)
(9) - верхняя и нижняя доверительные границы для
- верхняя и нижняя доверительные границы для  , соответствующие доверительной вероятности
, соответствующие доверительной вероятности