Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VIII . Решение дифференциальных уравнений
Обыкновенным дифференциальным уравнением называется уравнение
которое связывает независимый аргумент x, неизвестную функцию y и ее производные Решением дифференциального уравнения называется функция Уравнения с разделяющимися переменными Дифференциальное уравнение вида:
называется уравнением с разделенными переменными. Уравнение, которое приводится к данному виду, называется дифференциальным уравнением с разделяющимися переменными. Пример 8.1. Решить дифференциальное уравнение:
Решение.
Таким образом, получаем общий интеграл:
Однородные дифференциальные уравнения первого порядка Дифференциальное уравнение вида:
где Пример 8.2. Решить дифференциальное уравнение: Решение. Сделаем замену
Сделав обратную замену
Линейные дифференциальные уравнения первого порядка Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид
где Будем искать решение в виде Найдем сначала какое-либо частное решение
Тогда функция
Таким образом, решение исходного уравнения сводится к решению двух уравнений с разделяющимися переменными. Пример 8.3. Решить уравнение Решение. Разделив обе части уравнения на
Пусть
Положим
Уравнение Бернулли. Уравнение вида
называется уравнением Бернулли. Данное уравнение приводится к линейному с помощью подстановки Пример 8.4. Решить дифференциальное уравнение Решение. Сделаем замену
Сгруппируем второе слагаемое с третьим: Приравняем к нулю выражение в квадратных скобках и найдем функцию
Подставив
Отсюда
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.12.101 (0.008 с.) |
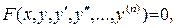
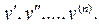 Порядком дифференциального уравнения называется максимальный порядок производной, входящей в уравнение.
Порядком дифференциального уравнения называется максимальный порядок производной, входящей в уравнение.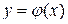 , которая при подстановке в уравнение превращает его в тождество. График этой функции называется интегральной кривой.
, которая при подстановке в уравнение превращает его в тождество. График этой функции называется интегральной кривой.

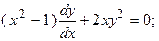
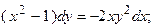
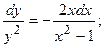



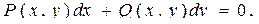
 и
и  – однородные функции одинакового измерения, называется однородным дифференциальным уравнением первого порядка. Данное уравнение можно привести к виду
– однородные функции одинакового измерения, называется однородным дифференциальным уравнением первого порядка. Данное уравнение можно привести к виду 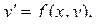 где
где  – однородная функция нулевого измерения. С помощью замены
– однородная функция нулевого измерения. С помощью замены 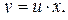 где
где 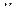 – новая неизвестная функция, рассматриваемое уравнение сводится к уравнению с разделяющимися переменными.
– новая неизвестная функция, рассматриваемое уравнение сводится к уравнению с разделяющимися переменными.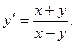
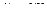 и получим:
и получим: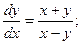


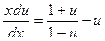 ;
;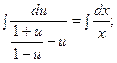
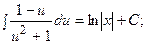

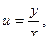 получим общий интеграл:
получим общий интеграл: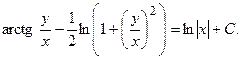
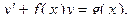
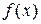 и
и 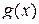 – некоторые (непрерывные) функции переменной
– некоторые (непрерывные) функции переменной  . В случае, когда функция
. В случае, когда функция 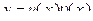 . Очевидно, что здесь искомыми становятся функции
. Очевидно, что здесь искомыми становятся функции  и
и 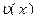 . Так как
. Так как 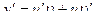 , то из определения следует
, то из определения следует  или
или 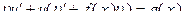
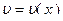 уравнения
уравнения
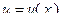 – решение уравнения
– решение уравнения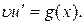

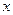 , получим линейное неоднородное уравнение:
, получим линейное неоднородное уравнение:
 , т.е.
, т.е. 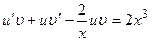 или
или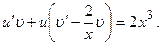
 или
или 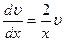 , откуда
, откуда  . Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при
. Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при 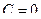
 и
и  . При
. При 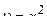 равенство
равенство 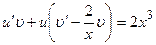 обратится в уравнение
обратится в уравнение  , или
, или 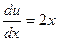 . Решая данное уравнение с разделяющимися переменными, получаем
. Решая данное уравнение с разделяющимися переменными, получаем 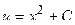 . Тогда окончательно имеем:
. Тогда окончательно имеем:
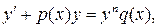 где
где 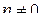
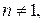
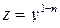 . Также можно использовать подстановку
. Также можно использовать подстановку 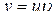 или метод вариации произвольных постоянных.
или метод вариации произвольных постоянных.
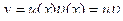 и получим
и получим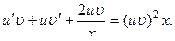
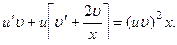 (
( )
)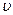 :
: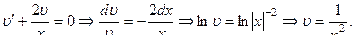
 :
: