Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие несобственного интеграла
Несобственным интегралом
Если предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае – расходящимся. Работая с несобственными интегралами, обычно выделяют две задачи: - исследование вопроса о сходимости заданного несобственного интеграла; - вычисление значения интеграла в случае, если он является сходящимся. Пример 6.4. Вычислить Решение. По определению Для нахождения интеграла, стоящего под знаком предела, используем формулу Ньютона – Лейбница:
Тогда
Таким образом, искомый несобственный интеграл сходится к 1. Если рассматривать несобственный интеграл на интервале
Если интегралы, входящие в правую часть равенства, сходятся, то рассматриваемый интеграл называется сходящимся, а если хотя бы один из интегралов правой части расходится, то – расходящимся. Пример 6.5. Вычислить Представим интеграл в виде суммы двух интегралов и исследуем их на сходимость, полагая
Вычислить несобственные интегралы (или установить их расходимость): 6.34. 6.36. 6.38. 6.40. 6.42. 6.44. 6.46. 6.48.
VII. Исследование на сходимость числовых рядов Общие признаки сходимости ряда: 1. Критерий Коши сходимости числового ряда. Для того, чтобы ряд
2. Необходимое условие сходимости ряда. Если ряд Признаки сходимости знакоположительных рядов Ряд
Общий признак сходимости знакоположительных рядов Для того, чтобы знакоположительный ряд
Признаки сравнения знакоположительных рядов Пусть даны два знакоположительных ряда 1) если 2) если существует 3) если
Признак Коши Пусть для знакоположительного ряда а) если б) если Примечание. Если
Признак Даламбера Пусть для знакоположительного ряда а) если б) если Примечание. Теорема не дает ответа на вопрос о сходимости ряда, если
Интегральный признак Коши Пусть члены ряда
Пример 7.1. Исследовать по признаку Даламбера сходимость ряда Решение. Зная,
Здесь, Пример 7.2. Исследовать по признаку Коши сходимость ряда Решение. Здесь
Пример 7.3. Исследовать по признаку сравнения сходимость ряда: Решение. Сравним данный ряд с гармоническим рядом: Каждый член Пример 7.4. Исследовать по признаку сравнения сходимость ряда: Решение. Сравним данный ряд с бесконечной геометрической прогрессией:
Пример 7.5. Исследовать по интегральному признаку сходимость ряда: Решение. Заменяем в заданном выражении общего члена ряда
Здесь несобственный интеграл расходится. Следовательно, согласно интегральному признаку, и данный ряд также расходится.
Исследовать на сходимость следующие ряды: 7.1. 7.3. 7.5. 7.7. 7.9. 7.11. 7.13. 7.15. 7.17. 7.19. 7.21. 7.23.
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.22.135 (0.039 с.) |
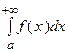 от функции
от функции 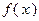 на полуинтервале
на полуинтервале 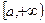 называется предел функции
называется предел функции  при
при 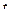 , стремящемся к
, стремящемся к 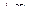 , т.е.
, т.е.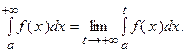
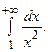
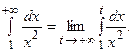
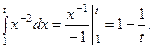
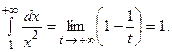
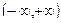 , то его можно представить как сумму двух интегралов, т.е.
, то его можно представить как сумму двух интегралов, т.е.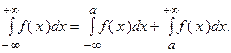
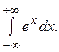
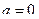 .
.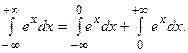
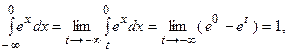 т.е. первый интеграл сходится к 1.
т.е. первый интеграл сходится к 1.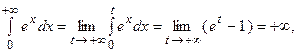 т.е. второй интеграл расходится, а, следовательно, расходящимся будет и несобственный интеграл
т.е. второй интеграл расходится, а, следовательно, расходящимся будет и несобственный интеграл 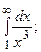 6.35.
6.35. 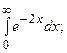
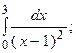 6.37.
6.37. 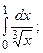
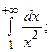 6.39.
6.39. 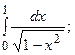
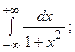 6.41.
6.41. 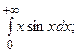
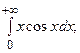 6.43.
6.43. 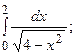
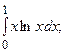 6.45.
6.45. 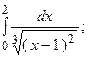
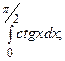 6.47.
6.47. 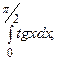
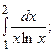 6.49.
6.49. 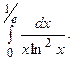

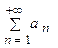 сходился, необходимо и достаточно, чтобы для любого
сходился, необходимо и достаточно, чтобы для любого 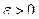 нашелся номер
нашелся номер 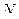 , такой, что для любых
, такой, что для любых 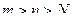 выполнялось условие
выполнялось условие 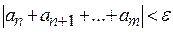 .
.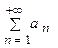 сходится, то его общий член стремится к нулю, т.е.
сходится, то его общий член стремится к нулю, т.е. 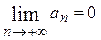 .
.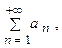 в котором все
в котором все 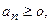 называется знакоположительным.
называется знакоположительным.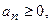 сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.
сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.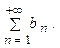 Тогда:
Тогда: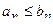 при всех
при всех 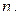 то из сходимости ряда
то из сходимости ряда 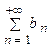 следует сходимость ряда
следует сходимость ряда 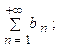
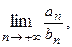 не равный нулю и конечный, то ряды
не равный нулю и конечный, то ряды 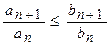 при всех
при всех 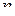 , то из сходимости ряда
, то из сходимости ряда 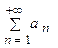 вытекает расходимость ряда
вытекает расходимость ряда 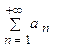 существует предел
существует предел 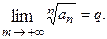 Тогда:
Тогда: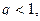 то ряд
то ряд 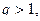 то ряд
то ряд 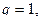 то теорема не дает ответа на вопрос о сходимости ряда.
то теорема не дает ответа на вопрос о сходимости ряда.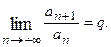 Тогда справедливы следующие утверждения:
Тогда справедливы следующие утверждения: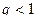 , то ряд
, то ряд 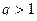 , то ряд
, то ряд 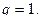
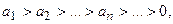 и пусть
и пусть 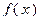 - непрерывная положительная убывающая функция, определенная при
- непрерывная положительная убывающая функция, определенная при 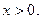 такая, что
такая, что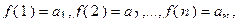 тогда интеграл
тогда интеграл 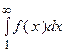 и ряд
и ряд 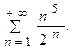
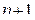 )-й член, заменяя в выражении
)-й член, заменяя в выражении 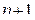 ). Затем ищем предел отношения последующего члена
). Затем ищем предел отношения последующего члена 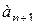 к предыдущему
к предыдущему 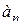 при неограниченном возрастании
при неограниченном возрастании 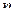
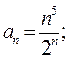
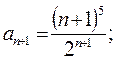
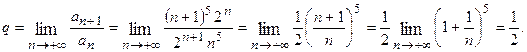
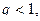 следовательно, согласно признаку Даламбера данный ряд сходится.
следовательно, согласно признаку Даламбера данный ряд сходится.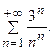
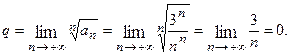
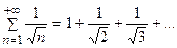
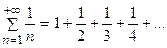
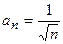 данного ряда, начиная со второго, больше соответствующего члена
данного ряда, начиная со второго, больше соответствующего члена 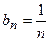 гармонического ряда:
гармонического ряда: 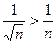 и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.
и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.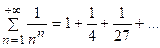
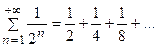 , которая представляет сходящийся ряд. Каждый член исследуемого ряда
, которая представляет сходящийся ряд. Каждый член исследуемого ряда 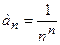 , начиная с третьего, меньше соответствующего члена
, начиная с третьего, меньше соответствующего члена 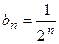 бесконечной геометрической прогрессии:
бесконечной геометрической прогрессии: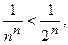 следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.
следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.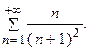
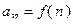 номер
номер 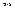 непрерывной переменной
непрерывной переменной 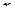 и убеждаемся, что полученная функция
и убеждаемся, что полученная функция 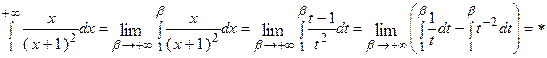

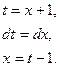
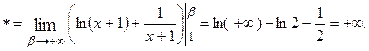
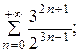 7.2.
7.2. 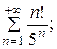
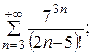 7.4.
7.4. 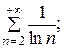
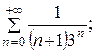 7.6.
7.6. 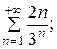
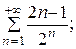 7.8.
7.8. 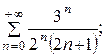
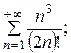 7.10.
7.10. 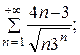
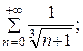 7.12.
7.12. 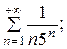
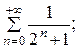 7.14.
7.14. 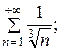
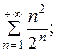 7.16.
7.16. 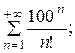
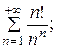 7.18.
7.18. 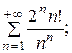
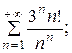 7.20.
7.20. 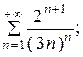
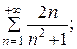 7.22.
7.22. 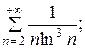
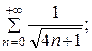 7.24.
7.24.