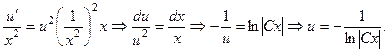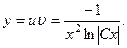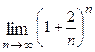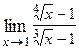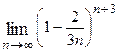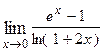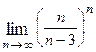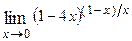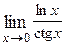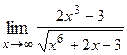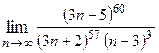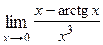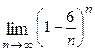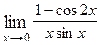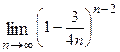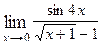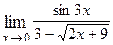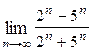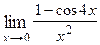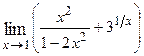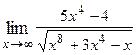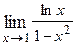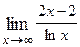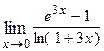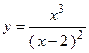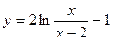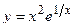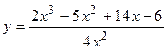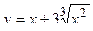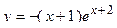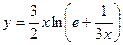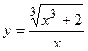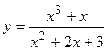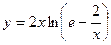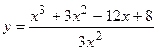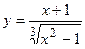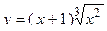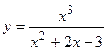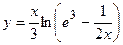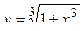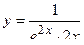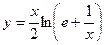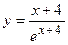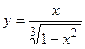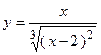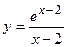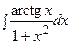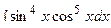Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I . Вычисление пределов функцииСодержание книги Поиск на нашем сайте
Введение В начале обучения студенты экономических и организационно – управленческих специальностей изучают курс высшей математики, который служит фундаментальной базой экономического и управленческого образования. Поэтому преподавание математических дисциплин для экономических и организационно – управленческих специальностей имеет следующие цели: ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических экономических и организационно – управленческих задач; привить умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести экономическую и организационно – управленческую задачу на язык математики. Кроме того, изучение курса математики имеет важное значение и для последующей практической работы экономиста и управленца, а также является необходимым для успешного изучения естественнонаучных, общепрофессиональных и специальных дисциплин. Настоящее учебно-методическое пособие предназначено для студентов очной и заочной форм обучения. Оно содержит более 400 задач по основным вопросам математического анализа: предел функции одной, производная функции, частные производные функции многих переменных, понятие градиента, исследование функций и построение графиков, неопределенный интеграл, определенный интеграл и геометрические приложения определенного интеграла, понятие несобственного интеграла, числовые ряды, дифференциальные уравнения. Подробно рассмотрены примеры решения некоторых типовых задач и представлены варианты контрольных заданий.
При подготовке настоящего пособия использованы примеры и задачи из следующих литературных источников: - Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1964. - Бохан К.А. и др. Курс математического анализа. Т.1.: Учебное пособие / Под ред. проф. Б.З. Вулиха. – М.: Просвещение, 1965. - Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1975. - Кундышева Е.С. Математика: Учебное пособие для экономистов. – 2-е изд. – М.: Издательско-торговая корпорация «Дашков Ко», 2006.
- Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова. – 2-е изд., испр. – М.: ИНФРА-М, 2008. - Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. Н.Ш. Кремера. – 3-е изд. – М.: ЮНИТИ-ДАНА, 2007.
Пример 4.2. 5. Случай, когда при В данном случае для нахождения предела функции используется 2-й замечательный предел:
е = 2,7182818… - основание натурального логарифма ln. Пример 5.1. Решение. При указанном изменении аргумента функция представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай
Пример 5.2. Решение. Полагаем
так как
6. Вычисление предела функции по правилу Лопиталя. Предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных, если он существует, или равен бесконечности.
Правило Лопиталя можно применять последовательно несколько раз, если это полезно, до получения результата. Пример 6.1. Пример 6.2. В примере 6.2 правило Лопиталя применено дважды.
Найти следующие пределы: 1.1. 1.3. 1.5. 1.7. 1.9. 1.11. 1.13. 1.15. 1.17. 1.19. 1.21. 1.23. 1.25. 1.27. 1.29.
1.31. 1.33. 1.35. 1.37. 1.39. 1.41. 1.43. 1.45. 1.47. 1.49. 1.51. 1.53. 1.55. 1.57. 1.59. 1.61. 1.63. 1.65. 1.67. 1.69. 1.71. 1.73. 1.75. 1.77. 1.79. 1.81. 1.83. 1.85. 1.87. 1.89. Таблица основных производных
Пользуясь формулами и общими правилами дифференцирования, найти производные следующих функций: 2.1. 2.3. 2.5. 2.7. 2.9. 2.11. 2.13. 2.15. 2.17. 2.19. 2.21. 2.23. 2.25. 2.27. 2.29. 2.31. 2.33. 2.35. 2.37. 2.39. 2.41. 2.43. 2.45. 2.47. Для нахождения производных показательно-степенных и некоторых алгебраических функций полезно бывает предварительно прологарифмировать функцию. Пример 2.1. Решение. Прологарифмируем заданную функцию, а затем найдем ее производную:
откуда
Пример 2.2. Решение.
2.49. 2.51. 2.53. Пример 4.1.
Пример 4.2.
Метод замены переменной Пример 4.3.
Пример 4.4.
Формула Ньютона – Лейбница Теорема. Пусть функция
Нахождение определенных интегралов с помощью формулы Ньютона – Лейбница осуществляется в два этапа: 1) используя методы вычисления неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); 2) применяя собственно формулу Ньютона – Лейбница, находят приращение первообразной, равное искомому интегралу. Пример 5.1. Вычислить
Признак Коши Пусть для знакоположительного ряда а) если б) если Примечание. Если
Признак Даламбера Пусть для знакоположительного ряда а) если б) если Примечание. Теорема не дает ответа на вопрос о сходимости ряда, если
Интегральный признак Коши Пусть члены ряда
Пример 7.1. Исследовать по признаку Даламбера сходимость ряда Решение. Зная,
Здесь, Пример 7.2. Исследовать по признаку Коши сходимость ряда Решение. Здесь Пример 7.3. Исследовать по признаку сравнения сходимость ряда: Решение. Сравним данный ряд с гармоническим рядом: Каждый член Пример 7.4. Исследовать по признаку сравнения сходимость ряда: Решение. Сравним данный ряд с бесконечной геометрической прогрессией:
Пример 7.5. Исследовать по интегральному признаку сходимость ряда:
Решение. Заменяем в заданном выражении общего члена ряда
Здесь несобственный интеграл расходится. Следовательно, согласно интегральному признаку, и данный ряд также расходится.
Исследовать на сходимость следующие ряды: 7.1. 7.3. 7.5. 7.7. 7.9. 7.11. 7.13. 7.15. 7.17. 7.19. 7.21. 7.23.
Уравнение Бернулли. Уравнение вида
называется уравнением Бернулли. Данное уравнение приводится к линейному с помощью подстановки Пример 8.4. Решить дифференциальное уравнение Решение. Сделаем замену
Сгруппируем второе слагаемое с третьим: Приравняем к нулю выражение в квадратных скобках и найдем функцию
Подставив
Отсюда
Варианты контрольных заданий Вычислить предел функции:
2. Исследовать функцию и построить её график:
3. Найти неопределенный интеграл:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.141.5 (0.013 с.) |

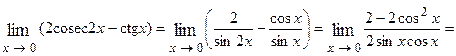
 или
или 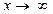 функция
функция  представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай
представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай 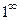 ).
).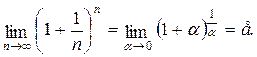
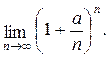
 , получим, что при
, получим, что при 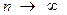
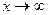 :
: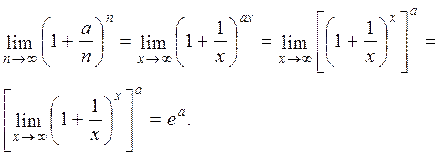
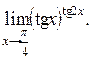
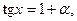 получим, что при
получим, что при 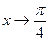
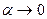 .
.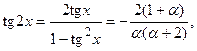
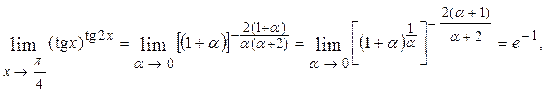
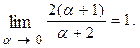
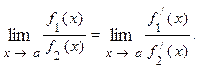
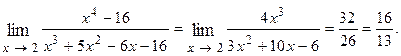
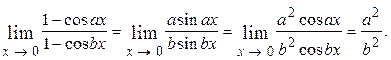
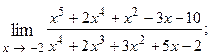 1.2.
1.2. 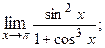
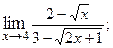 1.4.
1.4. 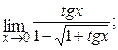
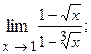 1.6.
1.6. 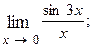
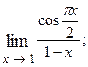 1.8.
1.8. 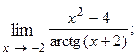
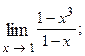 1.10.
1.10. 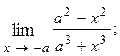
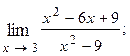 1.12.
1.12. 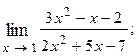
 1.14.
1.14. 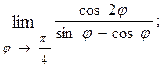

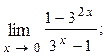 1.16.
1.16. 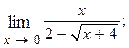

 1.18.
1.18. 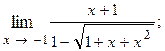
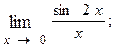 1.20.
1.20. 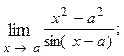
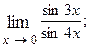 1.22.
1.22. 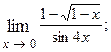
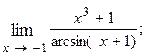 1.24.
1.24. 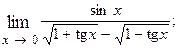
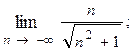 1.26.
1.26. 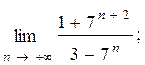
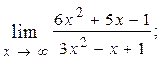 1.28.
1.28. 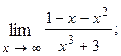
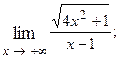 1.30.
1.30. 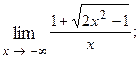
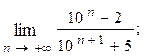 1.32.
1.32. 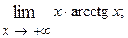
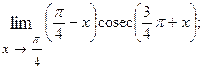 1.34.
1.34. 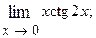
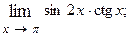 1.36.
1.36. 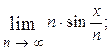
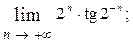 1.38.
1.38. 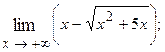
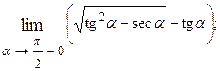 1.40.
1.40. 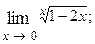
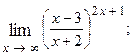
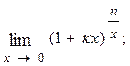
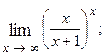 1.44.
1.44. 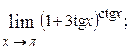
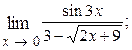 1.46.
1.46. 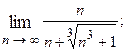
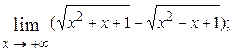 1.48.
1.48. 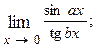
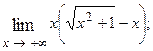 1.50.
1.50. 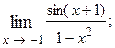
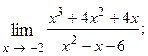 1.52.
1.52. 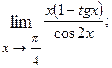
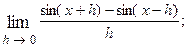 1.54.
1.54. 
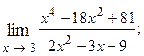 1.56.
1.56. 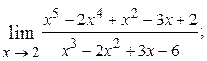
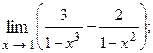 1.58.
1.58. 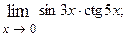
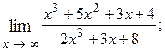 1.60.
1.60. 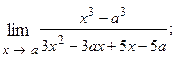
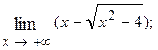 1.62.
1.62. 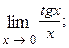
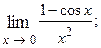 1.64.
1.64. 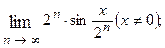
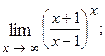 1.66.
1.66. 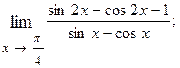
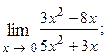 1.68.
1.68. 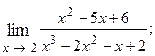
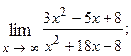 1.70.
1.70. 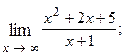
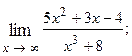 1.72.
1.72. 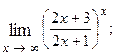
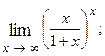 1.74.
1.74. 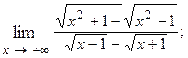
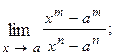 1.76.
1.76. 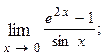
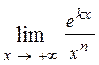 (k >0, n – натуральное число); 1.78.
(k >0, n – натуральное число); 1.78. 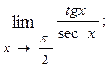
 1.80.
1.80. 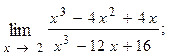
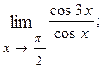 1.82.
1.82. 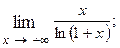
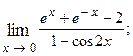 1.84.
1.84. 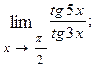
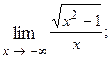 1.86.
1.86. 
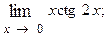 1.88.
1.88. 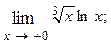
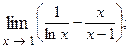 1.90.
1.90. 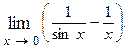
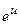
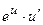
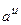


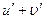
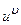
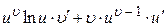
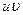
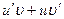
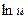
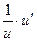
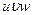
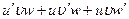
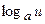
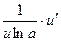
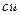
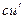
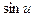
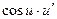
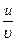
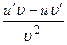
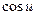
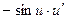
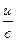
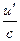
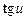
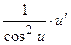
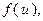
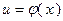
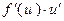
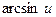

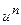
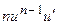
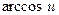
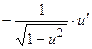
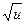
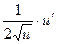
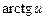
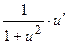

 2.2.
2.2. 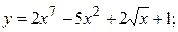
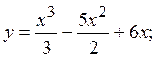 2.4.
2.4. 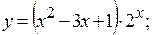
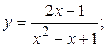 2.6.
2.6. 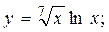
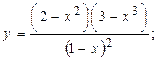 2.8.
2.8. 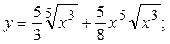
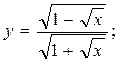 2.10.
2.10. 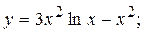
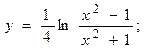 2.12.
2.12. 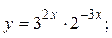
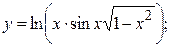 2.14.
2.14. 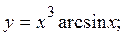
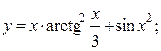 2.16.
2.16. 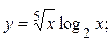
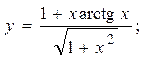 2.18.
2.18. 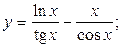
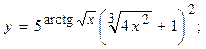 2.20.
2.20. 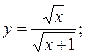
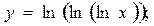 2.22.
2.22. 
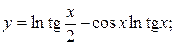 2.24.
2.24. 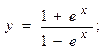
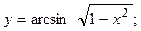 2.26.
2.26. 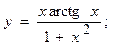
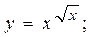 2.28.
2.28. 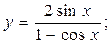
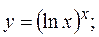 2.30.
2.30. 
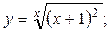 2.32.
2.32. 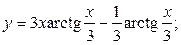
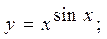 2.34.
2.34. 
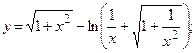 2.36.
2.36. 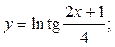
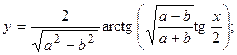 2.38.
2.38. 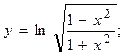
 2.40.
2.40. 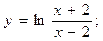
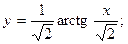 ; 2.42.
; 2.42. 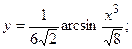
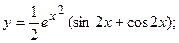 2.44.
2.44. 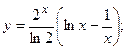
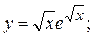 2.46.
2.46. 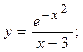
 2.48.
2.48. 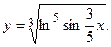
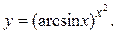

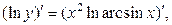
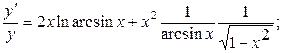
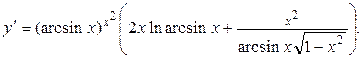
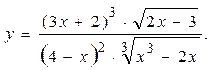
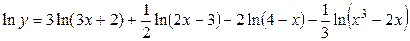 ;
;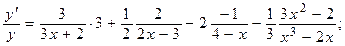 ;
;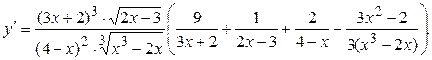 .
.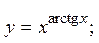 2.50.
2.50. 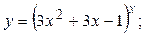
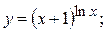 2.52.
2.52. 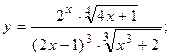
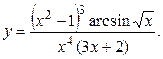
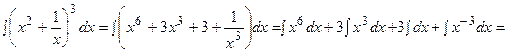
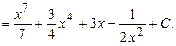
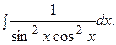 Так как
Так как 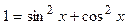 , то
, то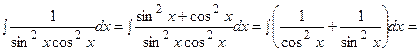
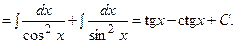
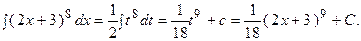
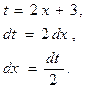

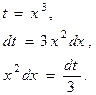
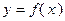 непрерывна на отрезке
непрерывна на отрезке 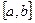 и
и 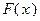 - любая первообразная для
- любая первообразная для 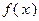 на
на 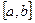 . Тогда определенный интеграл от функции
. Тогда определенный интеграл от функции  на
на 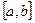 равен приращению первообразной
равен приращению первообразной 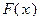 на этом отрезке, т.е.
на этом отрезке, т.е.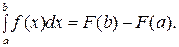

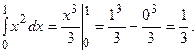
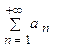 существует предел
существует предел 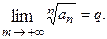 Тогда:
Тогда: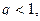 то ряд
то ряд 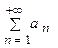 сходится;
сходится;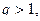 то ряд
то ряд 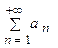 расходится;
расходится;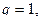 то теорема не дает ответа на вопрос о сходимости ряда.
то теорема не дает ответа на вопрос о сходимости ряда.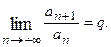 Тогда справедливы следующие утверждения:
Тогда справедливы следующие утверждения: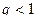 , то ряд
, то ряд 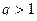 , то ряд
, то ряд 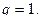
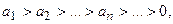 и пусть
и пусть 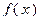 - непрерывная положительная убывающая функция, определенная при
- непрерывная положительная убывающая функция, определенная при 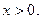 такая, что
такая, что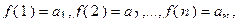 тогда интеграл
тогда интеграл 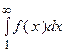 и ряд
и ряд 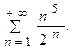
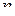 -й член ряда, находим следующий за ним (
-й член ряда, находим следующий за ним (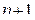 )-й член, заменяя в выражении
)-й член, заменяя в выражении 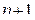 ). Затем ищем предел отношения последующего члена
). Затем ищем предел отношения последующего члена 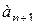 к предыдущему
к предыдущему 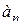 при неограниченном возрастании
при неограниченном возрастании 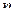
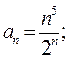
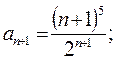
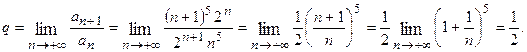
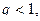 следовательно, согласно признаку Даламбера данный ряд сходится.
следовательно, согласно признаку Даламбера данный ряд сходится.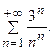
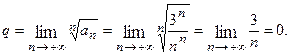
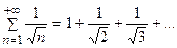
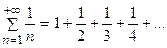
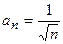 данного ряда, начиная со второго, больше соответствующего члена
данного ряда, начиная со второго, больше соответствующего члена 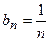 гармонического ряда:
гармонического ряда: 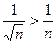 и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.
и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.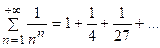
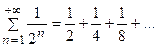 , которая представляет сходящийся ряд. Каждый член исследуемого ряда
, которая представляет сходящийся ряд. Каждый член исследуемого ряда 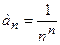 , начиная с третьего, меньше соответствующего члена
, начиная с третьего, меньше соответствующего члена 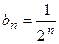 бесконечной геометрической прогрессии:
бесконечной геометрической прогрессии: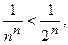 следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.
следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.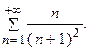
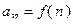 номер
номер 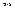 непрерывной переменной
непрерывной переменной 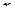 и убеждаемся, что полученная функция
и убеждаемся, что полученная функция 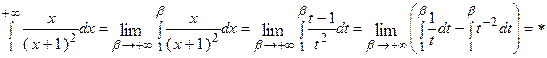

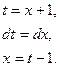
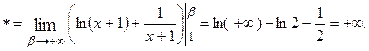
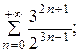 7.2.
7.2. 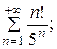
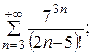 7.4.
7.4. 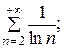
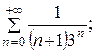 7.6.
7.6. 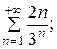
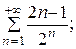 7.8.
7.8. 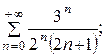
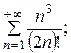 7.10.
7.10. 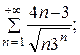
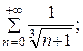 7.12.
7.12. 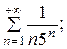
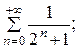 7.14.
7.14. 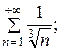
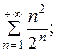 7.16.
7.16. 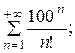
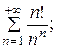 7.18.
7.18. 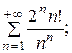
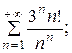 7.20.
7.20. 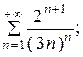
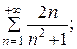 7.22.
7.22. 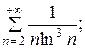
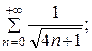 7.24.
7.24. 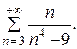
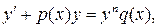 где
где 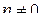
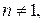
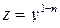 . Также можно использовать подстановку
. Также можно использовать подстановку 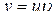 или метод вариации произвольных постоянных.
или метод вариации произвольных постоянных.
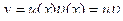 и получим
и получим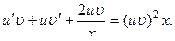
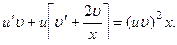 (
( )
)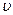 :
: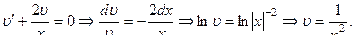
 :
: