
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое построение векторного произведения.
2) Чтобыгеометрически построить векторное произведение векторов a и b надо, совместив их начала, спроектировать вектор анна плоскость p, перпендикулярную вектору b. Полученную проекцию в плоскости, перпендикулярной вектору b, повернуть вокруг вектора b на 90°по ходу часовой стрелки, а затем умножить повернутый вектор на | b |. Алгебраические свойства векторного произведения. 1) a × b=-(b × a) – антикоммутативность; 2) λ(a × b)=λa × b=a ×λ b сочетательное (ассоциативное) относительно числового множителя; 3) a ×(b + с)= a × b + a × с -распределительное (дистрибутивное ) относительно суммы векторов; 4) a × а = 0 (a × а = |а||а| sin 0=0); Доказательства. 1) Пусть с = a × b, d =b × a. Если векторы a и b коллинеарны, то с = d =0. Если a и b не коллинеарны, то векторы с и d имеют одинаковую длину (|а||b| sinφ) и коллинеарны (т.к. оба ортогональны плоскости, определяемой векторами a и b). Но тогда либо с = d, либо с =- d. Если бы с=d, то обе тройки abc и bac были бы правыми, но они противоположной ориентации. Поэтому c=-d. ч.т.д. 2) Положим с=λ(a × b), d = λa × b. Исключим тривиальные случаи, когда вектор а коллинеарен вектору b или когда l=0. в этом случае с = d =0. Обозначим j= | с | = | l || a || b | sin y | d | = | l || a || b | sin j (10) Возможны 2 случая 1) j=y (когда l>0 и векторы а и l а направлены в одну сторону). 2) y=p-j (когда l<0 и векторы а и l а направлены в одну сторону). В обоих случаях sin y=sin j и в силу (10) |с|=|d|, т.е. векторы c и d имеют одинаковую длину. Далее, очевидно, что векторы c и d коллинеарны, т.к. ортогональность к плоскости, определяемой векторами l а и b, означает ортогональность и к плоскости, определяемой векторами а и b. Для доказательства равенства векторов c и d проверим, что эти векторы имеют одинаковое направление. Пусть l>0 (l<0), тогда векторы а и l а одинаково направлены (противоположно направлены), и, следовательно, векторы a × b и λa × b также одинаково (противоположно) направлены, а это означает, что векторы d =λ(a × b) и с= λa × b всегда одинаково направлены. ч.т.д.
3) – без доказательства. 4) – следует из того, что вектор а коллинеарен самому себе.
Теорема 7. Если два вектора определены своими декартовыми прямоугольными координатами а ={x1, y1, z1 }, b ={x2, y2, z2 }, то их векторное произведение имеет вид: a×b ={y1z2-z1y2,z1x2-x1z2, x1y2-y1x2} (11) a×b = Доказательство. В частности, i × i = j × j = k × k =0. i×i = j×j = k×k =0. i × j = k i × k =- j j × i =- k j×k = i k×i = j k×j =- i a×b =(x1 i +y1 j +z1 k)×( x2 i +y2 j +z2 k)= x1x2 i×i +x1y2 i×j +x1z2 i×k +y1x2 j×i +y1y2 j×j +y1z2 j×k +z1x2 k×i +z1y2 k×j +z1z2 j×j =0+x1y2 k +x1z2 (-j)+ y1x2 (-k)+ 0+y1z2 i+ z1x2 j+ z1y2 (- i)+ 0= =(y1z2-z1y2) i - (x1z2- z1x2) j +(x1y2 - y1x2) k = Если последний определитель равен 0, то либо один из векторов равен 0, либо векторы коллинеарны, т.е. их координаты пропорциональны. Пример. Найти векторное произведение векторов а =(1;3;4), b =(2;1;0) a×b =-4 i -8 j -5 k. Следствие. Если два вектора а ={x1, y1, z1 }, b ={x2, y2, z2 } коллинеарны, то их координаты пропорциональны, т.е. Доказательство. Из равенства нулю векторного произведения следует: y1z2=z1y2, x1z2=z1x2, x1y2=y1x2, а это эквивалентно доказываемым пропорциям.
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 47; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.178 (0.008 с.) |
 1) Если ненулевые векторы a и b ортогональны, то для геометрического построения вектора a × b достаточно совместить их начала и в плоскости, перпендикулярной вектору b, повернуть вектор а на 90° вокруг вектора b по ходу часовой стрелки, а затем умножить повернутый вектор на | b |.
1) Если ненулевые векторы a и b ортогональны, то для геометрического построения вектора a × b достаточно совместить их начала и в плоскости, перпендикулярной вектору b, повернуть вектор а на 90° вокруг вектора b по ходу часовой стрелки, а затем умножить повернутый вектор на | b |. , y=
, y= 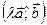 . По определению длины векторного произведения и произведения вектора на число можно утверждать, что
. По определению длины векторного произведения и произведения вектора на число можно утверждать, что Выражение векторного произведения через координаты векторов.
Выражение векторного произведения через координаты векторов.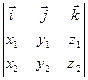 (11¢)
(11¢)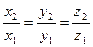 .
.


