
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические свойства векторного произведения.Содержание книги
Поиск на нашем сайте
Теорема 4. Два вектора являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю. Доказательство. Необходимость. Следует из определения векторного произведения, т.к. если векторы а и b коллинеарные, то угол между ними равен 0, а sin 0=0. Достаточность. Пусть a × b =0. покажем, что векторы а и b коллинеарные. Исключим тривиальный случай, когда хотя бы один из векторов Теорема 5. Длина (модуль) векторного произведения a × b равна площади параллелограмма, построенного на приведенных к общему началу векторах a и b. Доказательство. Следует из (7), т.к. площадь параллелограмма равна S= |а||b| sin(a^b) =| a × b|. Ч.т.д. Площадь соответствующего треугольника: SΔ=1/2 | a × b|. Определение. Ортом произвольного ненулевого вектора с называется единичный вектор, коллинеарный с и имеющий одинаковое с ним направление. Следствие. Если е – орт векторного произведения a × b, а S – площадь параллелограмма, построенного на приведенных к общему началу векторах a и b, то для векторного произведения a × b справедлива формула: a × b= S е (8). Замечание. Из определений орта и векторного произведения вытекает, что тройка abe является правой (т.к. тройка ab a × b является правой). Теорема 6. Если с – некоторый вектор, p - любая содержащая его плоскость, е – единичный вектор, лежащий в плоскости p и ортогональный к с, g – единичный вектор, ортогональный к плоскости p и направленный так, что тройка ес g является правой, то для любого лежащего в плоскости p вектора а справедлива формула a × с =пре а ×| с | g (9)
S=| a × с| - площадь построенного на приведенных к общему началу векторах а и с параллелограмма. Длина вектора, стоящего в правой части (9), равна |пре а | ×| с |, т.е. тоже равна S, т.к. если за основание указанного параллелограмма принять вектор с, то высота его h будет равна |пре а |.
Коллинеарность векторов, стоящих в левой и правой частях (9), вытекает из того, что оба эти вектора ортогональны плоскости p (вектор a × с в силу определения векторного произведения, а вектор пре а ×| с | g в силу того, что вектор g по условию ортогонален к плоскости p). Проверим, что векторы, стоящие в левой и правой частях (9) имеют одинаковое направление. Векторы a × с и g одинаково направлены (противоположно направлены), когда тройка a с g является правой (левой), т.е. когда векторы а и е лежат по одну сторону (по разные стороны) от с и проекция пре а является положительной (отрицательной), но это и означает, что векторы a × с ипре а ×| с | g всегда одинаково направлены. Ч.т.д.
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 79; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.125.158 (0.009 с.) |

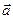 или
или 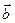 равен 0. Если оба вектора ненулевые, то
равен 0. Если оба вектора ненулевые, то 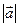 >0,
>0, 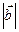 >0Þиз равенства a × b =0 и (7) следует, что sin j=0, т.е. векторы
>0Þиз равенства a × b =0 и (7) следует, что sin j=0, т.е. векторы 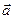 и
и  коллинеарны. Ч.т.д.
коллинеарны. Ч.т.д. Доказательство. Достаточно доказать, что векторы, стоящие в левой и правой частях (9): 1) имеют одинаковую длину, 2) коллинеарны, 3) имеют одинаковое направление.
Доказательство. Достаточно доказать, что векторы, стоящие в левой и правой частях (9): 1) имеют одинаковую длину, 2) коллинеарны, 3) имеют одинаковое направление.


