
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства проекции вектора на ось.Стр 1 из 4Следующая ⇒
Понятие базиса. Определение. Три линейно независимых вектора Определение. Два лежащих в плоскости p линейно независимых вектора Утверждения. 1) любая тройка некомпланарных векторов 2) любая пара лежащих в данной плоскости неколлинеарных векторов В дальнейшем для определенности будем рассматривать базис в пространстве. Пусть Покажем единственность разложения вектора Вычитая из (1) из (3) получаем: (l-l¢) В силу линейной независимости базисных векторов Теорема. При сложении двух векторов Доказательство. Пусть
a В силу единственности разложения по базису ч.т.д. Проекция вектора на ось. (Ортогональная) проекция точки на ось – основание перпендикуляра, опущенного из точки на данную ось. (рисунок)
 на ось u называется величина (длина) вектора на ось u называется величина (длина) вектора 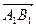 , проведенного из проекции начала в проекцию конца вектора , проведенного из проекции начала в проекцию конца вектора  , взятая со знаком “+”, если направление вектора , взятая со знаком “+”, если направление вектора 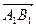 совпадает с направлением оси u и со знаком “-” в противном случае. совпадает с направлением оси u и со знаком “-” в противном случае.
Направляющие косинусы.
Числа cosα, cosβ, cosγ называются направляющими косинусами вектора Х=| Т.к. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то из равенств ОА=Х, ОВ=Y, OC=Z, получим выражение для длины вектора
Из (3) и (4) получаем:
Возводя в квадрат и складывая равенства (5), получаем: cos2α+cos2β+cos2γ=1. Т.к. вектор Действия над векторами.
Пусть 1) 2) Сумма (разность) векторов - вектор. Пусть
3) Умножение вектора на число- вектор: Примеры. а ={2; -3;0}, b ={1;3;-2}. a+2b={4;3;-4}.
. Приложение смешанного произведения. 1. Определение ориентации тройки векторов. Если abc>0, то тройка векторов, которая его образует, является правой. Если abc<0, то тройка векторов, которая его образует, является левой. 2. Определение компланарности векторов. 3. Вычисление объемов параллелепипеда и тетраэдра, построенного на векторах. Пример. Определить ориентацию тройки векторов ijk. ijk= Двойное векторное произведение. Пусть даны три произвольных вектора a, b и c. Если вектор b векторно умножается на вектор с, а вектор а также векторно умножается на векторное произведение b ´ c, то полученный при этом вектор а ´ (b ´ c)=[ a [ bc ]] называется двойным векторным произведением. Теорема. (Док-во на с.79). Для любых векторов a, b и c справедлива формула: а ´ (b ´ c)=[a[bc]]=b(ac)-c(ab) (13) Из формулы (13) Þ (а ´ b) ´ c =[[ ab ] c ]= b (ac)- a (bc) (13 ¢)
(Т.е. средний вектор, умноженный на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных.)
Понятие базиса. Определение. Три линейно независимых вектора Определение. Два лежащих в плоскости p линейно независимых вектора Утверждения. 1) любая тройка некомпланарных векторов 2) любая пара лежащих в данной плоскости неколлинеарных векторов В дальнейшем для определенности будем рассматривать базис в пространстве. Пусть Покажем единственность разложения вектора Вычитая из (1) из (3) получаем: (l-l¢) В силу линейной независимости базисных векторов Теорема. При сложении двух векторов Доказательство. Пусть
a В силу единственности разложения по базису ч.т.д. Проекция вектора на ось. (Ортогональная) проекция точки на ось – основание перпендикуляра, опущенного из точки на данную ось. (рисунок)
 на ось u называется величина (длина) вектора на ось u называется величина (длина) вектора 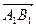 , проведенного из проекции начала в проекцию конца вектора , проведенного из проекции начала в проекцию конца вектора  , взятая со знаком “+”, если направление вектора , взятая со знаком “+”, если направление вектора 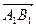 совпадает с направлением оси u и со знаком “-” в противном случае. совпадает с направлением оси u и со знаком “-” в противном случае.
Свойства проекции вектора на ось. 1) Проекция суммы (разности) двух векторов равна сумме (разности) проекций векторов на ось прu( 2) Постоянный множитель можно выносить за знак проекции:
Угол наклона вектора
На величину угла наклона вектора
Теорема. Проекция вектора Доказательство. Обозначим через v ось, проходящую через начало А вектора А1В1=АС (А1В1–величина вектора Но величина АС представляет собой проекцию вектора АС= Сопоставляя 91) и (20, получим Аффинные координаты (от лат. affinis – соседний, смежный). Аффинные координаты в пространстве определяются заданием базиса Аффинными координатами любой точки М называются координаты вектора Декартова прямоугольная система координат является частным случаем аффинной системы координат, отвечающей тройке взаимно ортогональных единичных базисных векторов.
Базисные векторы принято обозначать Любой вектор
Коэффициенты ах, ay, az называются декартовыми прямоугольными координатами вектора Если М – любая точка пространства, то декартовы координаты этой точки совпадают с декартовыми координатами вектора Координатами вектора Теорема. Декартовы прямоугольные координаты X,Y,Z вектора (Доказательство на стр. 61) Направляющие косинусы.
Числа cosα, cosβ, cosγ называются направляющими косинусами вектора Х=| Т.к. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то из равенств ОА=Х, ОВ=Y, OC=Z, получим выражение для длины вектора
Из (3) и (4) получаем:
Возводя в квадрат и складывая равенства (5), получаем: cos2α+cos2β+cos2γ=1. Т.к. вектор Действия над векторами.
Пусть 1) 2) Сумма (разность) векторов - вектор. Пусть
3) Умножение вектора на число- вектор: Примеры. а ={2; -3;0}, b ={1;3;-2}. a+2b={4;3;-4}.
.
|
||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.232 (0.211 с.) |
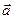 ,
,  и
и  образуют в пространстве базис, если любой вектор
образуют в пространстве базис, если любой вектор 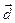 может быть представлен в виде некоторой линейной комбинации векторов
может быть представлен в виде некоторой линейной комбинации векторов  и
и 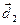 их координаты (относительно любого базиса
их координаты (относительно любого базиса  ,
, 
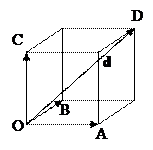 Обозначим буквами a, b, g углы наклона вектора
Обозначим буквами a, b, g углы наклона вектора 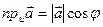 и предыдущей теоремы, получаем формулы для координат вектора
и предыдущей теоремы, получаем формулы для координат вектора  (4)
(4)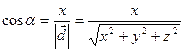 ;
;  ;
;  (5)
(5) ,
,  тогда
тогда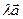 ={λх1,λу1,λz1}.
={λх1,λу1,λz1}. = 1>0 – правая тройка векторов.
= 1>0 – правая тройка векторов. )=
)= 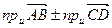

 на косинус угла φ наклона вектора
на косинус угла φ наклона вектора  оси v), т.к. оси u и v параллельны и одинаково направлены и отрезки этих осей заключенные между параллельными плоскостями a и b, равны. Т.к. по определению
оси v), т.к. оси u и v параллельны и одинаково направлены и отрезки этих осей заключенные между параллельными плоскостями a и b, равны. Т.к. по определению  , то получаем равенство:
, то получаем равенство:  =АС (1)
=АС (1) =
= 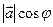 (2)
(2)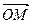 (относительно базиса
(относительно базиса  Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат.
Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат. - три взаимно ортогональных единичных вектора.
- три взаимно ортогональных единичных вектора. .
.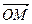 на плоскости
на плоскости 


