Photoshop - Урок 15. Эффекты текста

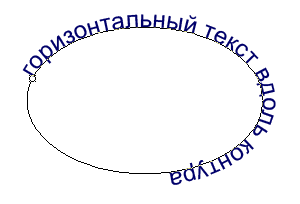
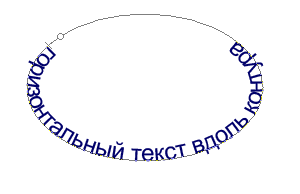
Можно выполнять различные действия с текстом для изменения его внешнего вида. Например, текст можно деформировать, преобразовать в различные фигуры или добавить к нему тень.

Текст по контуру

1. Создайте новый файл.
2. Создайте инструментом "Фигура" контур круга.
3. Возьмите инструмент "Горизонтальный текст". Установите курсор так, чтобы индикатор базовой линии инструмента "Текст" находился на контуре,
   
   
   
   и щелкните. После этого на контуре появится курсор вставки.
   
   

 

1. Введите текст, он будет располагаться вдоль контура.
   
   

 

1. Чтобы переместить текст вдоль контура, возьмите инструмент "Выделение контура" (черная стрелка), подведите курсор к контуру, он примет вид I-образной формы со стрелкой, нажмите левую клавишу мыши и ведите вдоль контура в сторону перемещения:
   
   

 

1. Чтобы отразить текст внутрь контура, возьмите инструмент "Выделение контура" (черная стрелка), подведите курсор к контуру, он примет вид I-образной формы со стрелкой, нажмите левую клавишу мыши и ведите поперек контура:
   
   

 

1. Чтобы изменить форму контура с текстом, возьмите инструмент "Стрелка" (белая стрелка), подведите курсор к контуру и щелкните по нему, появятся узловые точки, нажмите левой клавишей мыши на один из узлов и перетаскивайте до нужной формы:
   
   

Затем снова выровняйте текст по контуру, как в пункте 5.

 

1. Форму контура с текстом можно просто переместить инструментом "Перемещение".

 

Аналогично можно работать и с инструментами "Вертикальный текст", "Горизонтальный текст-маска" и "Вертикальный текст-маска".

Текст-маска

1. Создайте новый слой.

 

1. Возьмите инструмент "Горизонтальный слой-маска", выберите шрифт покрупнее (например, 60) и напишите им что-нибудь. При вводе текста появится красная маска:
   
   

 

1. По окончании ввода текста щелкните по галочке на панели параметров:
   
   

Границы текста превратятся в выделение:

 

1. Теперь можно залить буквы краской (Редактирование -> Выполнить заливку) или обвести их контур (Редактирование -> Выполнить обводку).
   
   

 

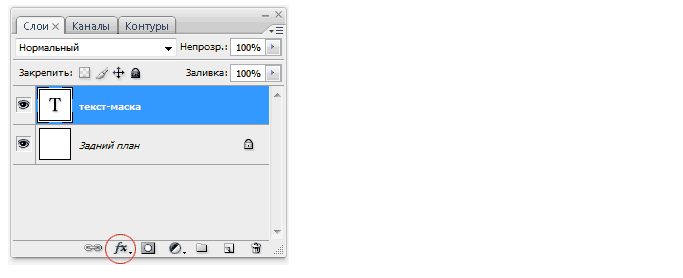
Аналогично можно работать и с инструментом "Вертикальный текст-маска".

Эффекты текстового слоя

Для придания тексту на изображении глубины можно добавить отбрасываемую тень или другие эффекты. Для этого:

1. На панели "Слои" выберите текстовый слой.

 

1. Щелкните два раза по этому слою или щелкните по кнопке "Добавить стиль слоя" внизу палитры слоев:
   
   

 

1. В открывшемся окне настройки эффектов поставьте галочки у тех эффектов, которые понравятся и щелкните ОК. Вот пример предыдущего текста с эффектами - тень и внутреннее свечение:
   
   

 

Текст также можно заполнить изображением. Об этом читайте на странице Создание и использование обтравочных масок. А еще к тексту можно применять различные фильтры и получать текст в виде огня, воды, железа и т.д. Подобные эффекты можно найти в разделе Adobe Photoshop - полезные навыки.

 

Фрактальная графика

 

Среди всех картинок, которые может создавать компьютер, лишь немногие могут поспорить с фрактальными изображениями, когда идет речь о подлинной красоте. У большинства из нас слово "фрактал" вызывает в памяти цветные завитушки, формирующие сложный, тонкий и составной узор. Но на самом деле этот термин имеет гораздо более широкий смысл. Фрактал - объект, обладающий бесконечной сложностью, позволяющий рассмотреть столько же своих деталей вблизи, как и издалека. Земля – классический пример фрактального объекта. Из космоса она выглядит как шаp. Если приближаться к ней, мы обнаружим океаны, континенты, побережья и цепи гор. Будем рассматривать горы ближе – станут видны еще более мелкие детали: кусочек земли на поверхности горы в своем масштабе столь же сложный и неровный, как сама гора. И даже еще более сильное увеличение покажет крошечные частички грунта, каждая из которых сама является фрактальным объектом.

Компьютеры дают возможность строить модели таких бесконечно детализированных структур. Есть много методов создания фрактальных изображений на компьютере. Два профессора математики из Технологического института штата Джоржия разработали широко используемый метод, известный как Cистемы Итерируемых Функций (СИФ). С помощью этого метода создаются реалистичные изображения природных объектов, таких, например, как листья папоротника, деревья, при этом неоднократно применяются преобразования, которые двигают, изменяют в размере и вращают части изображения. В СИФ используется самоподобие, которое есть у творений природы, и объект моделируется как композиция множества мельчайших копий самого себя. Фрактальные изображения с многоцветными завитушками относятся обычно к разряду так называемых фракталов с временным порогом, которые изображаются точками на комплексной плоскости с цветами, отражающими время, требуемое для того, чтобы орбита данной точки перешла ("перебежала") определенную границу. Комплексная плоскость - как координатная плоскость с осями x и y. По паре координат точка строится на комплексной плоскости так же, как и точка на плоскости Oxy, но числа имеют другой, необычный смысл: они обладают мнимой компонентой, называемой i, которая равна квадратному корню из -1. (Вот почему i - мнимая единица - в действительности корень из -1 не существует). Это искажает обычные правила математики, так что такие общепринятые операции как умножение двух чисел, дают необычные результаты.

Наиболее известный фрактал, множество Мандельброта – фрактал с временным порогом. Для каждой точки на экране компьютер считает координаты серии точек, определяющих мнимый путь, называемый орбитой. Точки, чьи орбиты никогда не выходят за пределы мнимого цилиндра, расположенного в начале координат комплексной плоскости, считаются элементами множества Мандельброта и обычно закрашиваются черным. Точки, чьи орбиты выходят за пределы цилиндра, раскрашиваются в соответствии с быстротой "убегания": пиксель, чья орбита покидает цилиндр, например, на шестой итерации, можно раскрасить голубым, a тот - орбите которого требуется для этого семь итераций - красным. В результате на изображении получим множество Мандельброта и его окружение с "нестабильными" областями фрактала - областями, для которых малые изменения формулы ведут к большой разнице в орбитальном поведении. Это характеризуется густотой закраски рисунка. Меняя формулу для подсчета орбит, получим другие, такие же экзотические фракталы с временным порогом. Бесконечно детализированная структура множества Мандельброта становится "ясной", когда вы увеличиваете произвольную область. Неважно, сколь маленький участок вы рассматриваете: рисунок, который вы увидите, будет одинаково сложным. Почему? Потому что в двумерной плоскости, на которой строится множество Мандельброта, любая область содержит бесконечное число точек. Когда вы выбираете область для отображения, компьютер точкам из области ставит в соответствие точки на экране. И каждая точка, выбранная как угодно близко к другой, имеет свою характеристическую орбиту, порождающую соответствующий цветовой узор.

Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.

Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.

Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале.

В центре фрактальной фигуры находится её простейший элемент - равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.

Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом, можно описать и такой графический элемент, как прямую. Изменяя и комбинирую окраску фрактальных фигур можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также, составлять из полученных фигур «фрактальную композицию». Фрактальная графика, также как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется.

Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы. Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект»; «Фрактальная прямая»; «Фрактальная композиция»; «Объект-родитель» и «Объект наследник». Следует обратить Ваше внимание на то, что фрактальная компьютерная графика, как вид компьютерной графики двадцать первого века получила широкое распространение не так давно. Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать такие композиционные приёмы как, горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение?

Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную структуру. Это свойство фрактального объекта может быть удачно использовано при составлении декоративной композиции или для создания орнамент. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу. С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной графике найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные.

Геометрические фракталы на экране компьютера - это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.

Создатель фракталов - это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности - Painter) от прочих графических программ.

Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.

 

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основная литература

1. Гурский Ю.А., Гурская И. Компьютерная графика: Photoshop CS 3, CorelDRAW X3, Illustrator CS 3. Трюки и эффекты (+CD). http://www.twirpx.com/file/698565/

2. Микрюков В.Ю. Компьютерная графика: учеб. пособие для СПО. http://lib.omgpu.ru/cgi-bin/irbis64r/cgiirbis_64.exe

3. Писарев А.П. Электронное пособие и лаб. практикум по КГ(векторная графика и растровая графика)

Дополнительная литература

1. Михеева Е.В. Информатика: учеб. пособие для СПО. – М.: Академия, 2009.

Интернет-ресурсы

1. Руденко К.А. "Учебник Фотошоп" - раздел для начинающих [Электронный ресурс]. Режим доступа: http://www.photoshop-master.ru/articles.php.

2. Гурский Ю.А. Онлайн учебник Corel Draw и PhotoPaint [Электронный ресурс]. Режим доступа: http://www. academia-moscow.ru›off-line/_books.