
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы компьютерного моделирования сварочных процессовСтр 1 из 18Следующая ⇒
Глава 12 Методы компьютерного моделирования сварочных процессов
Уравнение сохранения заряда. Первое правило Кирхгофа В основе решения задачи лежит уравнение сохранения заряда. Заряд не накапливается в участках электрической цепи, поэтому сумма токов, втекающих в каждый узел, равна нулю (первое правило Кирхгофа)
Например, для узла 1
где Мы получили уравнение (12.5), в котором несколько неизвестных – потенциал узла 1 и смежных с ним узлов 2, 3, 4 и 5. Это - уравнение постоянства заряда в узле 1. Такое уравнение можно записать для каждого узла, поэтому число уравнений равно общему количеству неизвестных. Вместе они образуют систему линейных уравнений:
которая в сокращенной (тензорной) форме записи выглядит как
где Мы проследили всю типичную процедуру метода конечных элементов от вывода исходных уравнений на основе некоторого дифференциального уравнения до сведения их в систему линейных уравнений. Далее необходимо решить систему и найти неизвестные, а по ним – все остальные параметры модели. В данном случае исходное дифференциальное уравнение сохранения заряда – это уравнение Лапласа (12.2). Его можно превратить в систему алгебраических уравнений, если вместо производных подставить отношение конечных разностей:
Можно сказать, что каждое уравнение в системе (12.6) – это проинтегрированное по некоторой области (по одной ячейке) дифференциальное уравнение (12.2). При интегрировании появляются неопределенные константы, которые нужно установить из граничных условий для получения окончательного решения. Граничными условиями являются значения функции в соседних узлах. Смысл системы уравнений заключается в стыковке между собой полученных интегралов по всем ячейкам.
Свойства системы уравнений Матрица
В каждой строке данной матрицы самый большой коэффициент находится на главной диагонали, и он положителен. Остальные коэффициенты отрицательны и меньше по абсолютной величине. Сумма коэффициентов в каждой строке равна нулю. Действительно, если потенциалы смежных ячеек равны
то все токи будут равны нулю. Подставим (12.8) в уравнение (12.5)
откуда
Таким образом, матрица является положительно определенной. Это обеспечивает устойчивость решения системы методом Гаусса. Матрица разреженная, в ней много нулевых коэффициентов: Очень важным моментом является однородность системы уравнений (в правой части - нули). Это значит, что она всегда имеет решение Возможно, система имеет также нетривиальное решение с разными Если в другом узле Условием 2-го рода является подача тока от внешнего источника в какой-то из узлов. Этот ток добавляется к правой части соответствующего уравнения.
Устойчивость решения В процедуре метода Гаусса есть операция деления каждого уравнения на первый коэффициент. Вначале первое уравнение делят на Этого можно избежать, переставляя местами уравнения. Если сперва исключить то неизвестное, при котором диагональный коэффициент Понятие вырожденной матрицы поясняет рис. 12.4, где рассмотрено решение системы из двух уравнений, каждое уравнение изображается прямой линией на графике, по осям которого отложены значения неизвестных. Решение отображает точка пересечения прямых. Если матрица близка к вырожденной (ее определитель близок к нулю), то прямые пересекаются под острым углом. Это не мешает найти решение при отсутствии погрешностей в значениях коэффициентов матрицы и процедуре решения. Однако появление данных погрешностей, даже небольших, (на рисунке это показано заменой прямых на полосы, ширина которых характеризует погрешность) приводит к резкому увеличению погрешности результата решения. Причинами вырождения матрицы могут быть особенности геометрии модели, свойств материала и граничных условий. У вырожденной матрицы (определитель равен нулю) линии становятся параллельными (решение отсутствует) или совпадают (бесчисленное множество решений).
Рис. 12.4. Схема роста погрешности решения при вырождении матрицы
Итерационные методы решения Возможны два пути применения итераций при решении системы уравнений. I. Итерационное решение системы уравнений (применяется вместо метода Гаусса). Порядок итераций такой (см. схему на рис. 12.3): 1) Задаемся начальными значениями потенциала в точках 1, 2, 3 …, например 2) Проводим итерационное уточнение значений потенциала, для этого обходим по очереди все точки модели: - у точки 1 в уравнение постоянства заряда входят значения в точках со второй по пятую; поскольку все они имеют нулевой потенциал, значение в точке 1 после первой итерации не изменится: - у точки 2 среди соседей есть точки A и B, потенциалы которых - пройдя по остальным точкам, убедимся, что в них потенциал не изменится: 3) Теперь будем считать - в точке 1 потенциал изменится - в точке 2 потенциал не изменится
- из остальных точек потенциал изменится в точке 3 4) Такой перебор всех точек будем повторять, пока хотя бы в одной из них будет происходить изменение потенциала. Итерации прекращаются, когда эти изменения за итерацию станут меньше заданного уровня точности
Достоинствами этого метода являются простота (уравнения составляются и решаются поочередно, полная система уравнений не составляется) и устойчивая сходимость при любом числе неизвестных. Его недостаток необходимость многократных обходов и медленная сходимость (особенно вначале, если исходное приближение выбрано неудачно). Разновидностью данного метода является метод Зейделя, в котором применение найденных значений неизвестных производится сразу, а не со следующей итерации. II. Итерационное уточнение решения, полученного методом Гаусса. Чтобы организовать итерационный процесс, нужно представить искомое значение на итерации в виде суммы значения на предыдущей итерации и приращения за итерацию:
Подставив это выражение в систему уравнений (12.7), получим:
Это система уравнений относительно Ход итерационного процесса такой: 1) Задаемся начальными значениями потенциала 2) Находим из решения системы (12.13) 3) Если после подстановки этих значений в исходные уравнения (12.7) получаем тождества, то найденные значения являются точными, и итерации прекращаются. Если же невязка 4) Условием завершения итераций является уменьшение до заданного порога либо невязки Уравнение Фурье Уравнение Фурье
является аналогом закона Ома (12.1): вместо плотности электрического тока
Теплота распространяется от горячих частей тела к холодным (в сторону убывания температуры), поэтому в уравнении присутствует знак минус. Поток тепла пропорционален градиенту температур, т. е. разности температур на единицу длины в направлении потока теплоты, и зависит от свойств материала (теплопроводности). Размерность теплопроводности – Вт/(м·К). Если имеется ячейка (элементарный объем) и найдены потоки теплоты через все ее границы, то общее количество теплоты, поступившего в объем за время
где Чтобы определить температуру, нужно найти изменение количества теплоты (энергии)
Изменение температуры при изменении теплосодержания зависит от теплоемкости вещества. Удельная теплоемкость – это количество теплоты, необходимое для повышения температуры единицы массы вещества на
Уравнение теплопроводности (уравнение Пуассона) имеет вид:
где Температурное поле является нестационарным. В отличие от протекания электрического тока, о температуре нельзя сказать, что ее изменения происходят только тогда, когда изменяются граничные условия. Наиболее очевидно это для стадии остывания, когда сварка закончена, все граничные условия постоянны, а температура продолжает изменяться. При этом протекают 2 процесса: - выравнивание температуры между точками тела; - остывание (выравнивание температуры между телом и окружающей средой). Температура передается от точки к соседним точкам, поэтому при моделировании применима явная схема: следующее состояние точки можно определить по текущему состоянию данной и соседних с ней точек.
Метод элементарных балансов В литературе по численным методам расчета тепловых процессов существует понятие «модель из теплоемких масс и теплопроводящих стержней». Речь идет именно о тех принципах, которые реализованы в программном комплексе «Сварка». Ту электрическую схему, которой мы заменяли деталь из электропроводного материала, можно назвать «моделью из электропроводящих стержней». Каждый элемент (граница ячеек = электропроводящий стержень) соединяет две ячейки (два узла). Нашу тепловую модель можно представить такими эквивалентными схемами (рис. 12.11).
Рис. 12.11. Схемы моделей для задач энергомассопереноса: из конденсаторов и сопротивлений (а); из масс и стержней (б): R - сопротивление, C - электроемкость конденсатора,
Суть метода элементарных балансов состоит в том, что две соседние ячейки обмениваются теплотой через границу, причем сколько теплоты уходит из одной ячейки, столько же приходит в другую. Важной особенностью метода является его консервативность, т. е. точное соблюдение закона сохранения энергии. Отличием задач электропроводности и теплопроводности является сочетание свойств. Теплоемкость материала является существенной (это на схеме подчеркнуто добавлением конденсаторов в каждом ее узле), а теплопроводность относительно невысокой, поэтому переходные процессы выравнивания температур занимают продолжительное время, и их необходимо моделировать. При моделировании переходных процессов может быть рациональным применение явной схемы.
Неявная схема решения В некоторых случаях мелкая сетка элементов не связана с большими градиентами температуры и высокой скоростью переходных тепловых процессов. Тогда переход на неявную схему позволяет существенно увеличить шаг решения без потери точности и сократить машинное время решения задачи. Каждый шаг по неявной схеме требует существенно больших вычислительных затрат, поэтому переход на нее может быть оправдан при укрупнении шага решения не менее, чем на порядок. Согласно (2.24), в каждой внутренней ячейке
где N – количество границ ячейки. В этом выражении, в отличие от (12.24), потоки тепла записаны не для начала, а для конца текущего шага решения. Если ячейка имеет наружные границы с условиями 2 и 3 рода, то добавляются потоки тепла через эти границы:
Получаем систему уравнений относительно неизвестных температур конца шага
Диагональные коэффициенты матрицы проводимости
внедиагональные коэффициенты матрицы
Правая часть – вектор поступившей теплоты
Узлы, в которых заданы граничные условия 1 рода
Поскольку свойства материала определяются для температуры начала шага, большие изменения температуры за шаг могут вызывать погрешности при нелинейности свойств. В этом случае требуется итерационная процедура для уточнения полученного решения. Теория деформаций Существует три вида движения твердого тела (рис. 12.14): поступательное, вращательное и деформационное (изменение расстояний между точками тела). Изменение линейных размеров называется линейной деформацией, а изменение угловых размеров - угловой.
Рис. 12.14. Схема перемещений и деформаций твердого тела
Всего в каждом элементарном объеме тела могут присутствовать три компоненты линейной деформации по трем осям и три компоненты угловой деформации. Для сокращения количества аналогичных формул используют тензорную форму записи:
Компоненты линейной деформации выражают через изменения длины отрезков в теле (разности перемещений их концов):
Общая формула:
Компоненты угловой деформации выражают через разности перемещений концов отрезков, направленных по нормали к этим отрезкам:
Это угол взаимного поворота двух перпендикулярных отрезков. При малых значениях перемещений формулу можно упростить:
Введя обозначение
Это средние деформации по длине отрезков
Формулы (12.29-12.31) просты (устанавливают линейную зависимость деформаций от перемещений), но приводят к погрешности при поворотах тела как единого целого. По этим формулам поворот выглядит как сжатие. Рассмотрим изменение длины
Рис. 12.15. Искажение деформации при повороте тела
Из рис. 12.15 видно, что в гибких стержнях и оболочках даже малых деформациях могут возникать большие перемещения (из Формула, исключающая ложные деформации от поворота тела или его фрагмента в пространстве:
В этой формуле применена сокращенная тензорная запись скалярного произведения векторов, выражение
Для линейной деформации из (12.32) получаем
Формула (12.32) дает компоненты деформации в системе координат, связанной с волокнами материала. В результате перемещений точек эта система поворачивается в пространстве относительно исходной системы координат. Компоненты поворота, найденные по формулам
позволяют рассчитать компоненты деформации в исходной системе координат. Деформацию, измеренную по отношению к исходным размерам тела
а по отношению к размерам тела после его деформирования
Истинные деформации, или деформации Генки, определяют по отношению к текущим размерам тела, меняющимся в процессе деформирования:
Для этого необходимо разбить процесс на бесконечно мелкие шаги и найти деформацию интегрированием от
Различие между тремя видами деформации становится существенным при Деформации Коши и Альманси несимметричны при растяжении и сжатии. Если отрезок длиной Совокупность компонент деформации называют тензором:
Тензор – это вектор второго порядка, характеризуемый величиной и парой направлений (каждая компонента деформации связана с двумя осями, вдоль одной оси направлен отрезок, вдоль другой – перемещение конца отрезка). Закон парности касательных деформаций, являющийся следствием формул (12.31) и (12.32):
сокращает число независимых компонент тензора до шести. Три параметра характеризуют ориентацию главных осей деформации в выбранной системе координат, а три других (инварианты) характеризуют деформированное состояние и не зависят от выбора системы координат. Первый инвариант тензора
где Шаровой тензор соответствует состоянию всестороннего равноосного растяжения или сжатия, при котором изменяется объем тела без изменения его формы:
Найдя первый инвариант любого тензора, можно выделить из него шаровую составляющую (шаровой тензор):
Девиатор тензора может быть найден путем вычитания из него шаровой составляющей. Девиатор деформации
Компоненты тензора зависят от выбора осей. Если в системе координат
то такие оси и компоненты деформации называют главными:
У шарового тензора все оси главные. Угловые деформации при повороте осей на
Рис. 12.16. Связь линейных и угловых деформаций
Всего тензор имеет шесть независимых параметров, в том числе три инварианта. Полный комплект инвариантов включает три параметра. Примеры таких комплектов: Главные деформации
или
Способ нахождения главных компонент: 1) имеются формулы расчета инвариантов
2) найдя инварианты, нужно составить и решить кубическое уравнение (12.47). Один из важнейших инвариантов девиатора деформации – интенсивность деформации:
Любая деформация представляет собой изменение формы и размеров элементарного объема материала. Если в исходном состоянии этот объем имел форму сферы и радиус Первый инвариант деформации показывает изменение объема эллипсоида (независимо от формы и соотношения осей), второй - суммарное изменение формы (сумму квадратов отклонений точек эллипсоида от эквивалентной по объему сферы). Третий инвариант, например параметр Лодэ
показывает особенности формы эллипсоида: если Деформированное состояние можно изобразить в виде кругов Мора (рис. 12.17). Значение первого инварианта (объемной деформации) отображает расположение кругов на оси
Рис. 12.17. Круги Мора для линейных и угловых деформаций (
Теория напряжений Механическим напряжением σ называется отношение силы P, действующей между двумя частями твердого тела, к площади A разделяющей их поверхности (рис. 12.18):
Рис. 12.18. Схема определения нормального и касательного напряжений
По размерности напряжение аналогично давлению и измеряется в мегапаскалях: Если поверхность плоская, а сила перпендикулярна плоскости (действует по нормали к ней), напряжение называется нормальным:
а если сила действует вдоль плоскости (по касательной), напряжение называется касательным:
Нормальная сила аналогична силе давления, а касательная – силе трения. В общем случае сила P направлена под углом к поверхности и может быть разложена на составляющие
| Поделиться:
| |
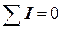 . (12.4)
. (12.4)
 ;
; ;
; ;
; , (12.5)
, (12.5)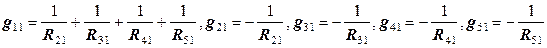 .
.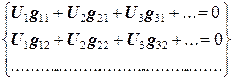 , (12.6)
, (12.6)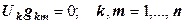 , (12.7)
, (12.7)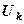 - вектор неизвестных потенциалов в узлах,
- вектор неизвестных потенциалов в узлах,  - матрица
- матрица  системы уравнений,
системы уравнений,  - порядок матрицы (число неизвестных и уравнений в системе). При тензорной записи пропускают знак суммы. На то, что в выражении (12.7) записан не одночлен, а сумма одночленов, указывает «слепой» - повторяющийся два раза индекс k, по которому и производят суммирование.
- порядок матрицы (число неизвестных и уравнений в системе). При тензорной записи пропускают знак суммы. На то, что в выражении (12.7) записан не одночлен, а сумма одночленов, указывает «слепой» - повторяющийся два раза индекс k, по которому и производят суммирование. .
. традиционно называется матрицей жесткости (потому что МКЭ создавали для задач механики), но в данном случае это матрица проводимости
традиционно называется матрицей жесткости (потому что МКЭ создавали для задач механики), но в данном случае это матрица проводимости  . Эта матрица симметричная:
. Эта матрица симметричная: .
. , (12.8)
, (12.8) ,
,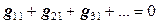 ,
, .
.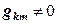 только если узлы
только если узлы 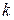 и
и  - смежные. Если удачно пронумеровать узлы, то ненулевые элементы соберутся в ленту около главной диагонали (получим ленточную матрицу). Остальные элементы можно не хранить, т. е. экономить память компьютера. Кроме того, вследствие симметрии матрицы достаточно хранить только половину ленты.
- смежные. Если удачно пронумеровать узлы, то ненулевые элементы соберутся в ленту около главной диагонали (получим ленточную матрицу). Остальные элементы можно не хранить, т. е. экономить память компьютера. Кроме того, вследствие симметрии матрицы достаточно хранить только половину ленты.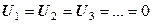 . Кроме того, мы установили, что
. Кроме того, мы установили, что  также будет решением при любом
также будет решением при любом  . Такие решения называются тривиальными.
. Такие решения называются тривиальными. . Для этого нужно исключить из системы одно уравнение (поскольку значение в одном из узлов известно) или заменить его (что то же самое) на
. Для этого нужно исключить из системы одно уравнение (поскольку значение в одном из узлов известно) или заменить его (что то же самое) на  (см. рис. 12.2). После этой процедуры система перестает быть однородной (в остальных уравнениях появится правая часть
(см. рис. 12.2). После этой процедуры система перестает быть однородной (в остальных уравнениях появится правая часть 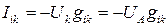 ). Если других условий нет, то решение системы уравнений даст во всех узлах одинаковый потенциал
). Если других условий нет, то решение системы уравнений даст во всех узлах одинаковый потенциал 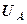 .
. , получим разные потенциалы во всех узлах.
, получим разные потенциалы во всех узлах.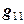 , потом второе на
, потом второе на 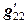 и т. д, но
и т. д, но  (если
(если  ). По мере исключения неизвестных коэффициенты на главной диагонали
). По мере исключения неизвестных коэффициенты на главной диагонали 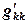 уменьшаются, и к тому моменту, когда происходит деление, может произойти уменьшение
уменьшаются, и к тому моменту, когда происходит деление, может произойти уменьшение  , и после деления на нуль решение полностью нарушается. Иногда получается не 0, а просто большой рост погрешности.
, и после деления на нуль решение полностью нарушается. Иногда получается не 0, а просто большой рост погрешности.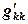 самый большой, то из других уравнений будут вычитаться маленькие числа и устойчивость решения повысится. К счастью, в большинстве случаев матрица
самый большой, то из других уравнений будут вычитаться маленькие числа и устойчивость решения повысится. К счастью, в большинстве случаев матрица  оказывается положительно-определенной и невырожденной, т. е. решение идет устойчиво без дополнительных усилий.
оказывается положительно-определенной и невырожденной, т. е. решение идет устойчиво без дополнительных усилий.
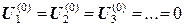 (кроме А, В,…, в которых потенциал известен).
(кроме А, В,…, в которых потенциал известен). ;
; и
и 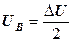 известны, а
известны, а 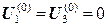 , по этим данным из уравнения постоянства заряда можно найти
, по этим данным из уравнения постоянства заряда можно найти  ;
;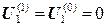 .
.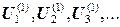 новыми значениями в т. 1, 2, 3 и повторим итерационное уточнение значений потенциала:
новыми значениями в т. 1, 2, 3 и повторим итерационное уточнение значений потенциала: , поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2;
, поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2;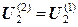 , поскольку на предыдущей итерации не изменялся потенциал в смежных с ней точках A, B, 1 и 3;
, поскольку на предыдущей итерации не изменялся потенциал в смежных с ней точках A, B, 1 и 3; , поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2.
, поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2.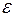 :
:
 . (12.12)
. (12.12) ;
;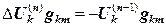 . (12.13)
. (12.13) , аналогичная (12.7), но с правой частью. Выражение в правой части представляет собой невязку (погрешность) после предыдущей итерации.
, аналогичная (12.7), но с правой частью. Выражение в правой части представляет собой невязку (погрешность) после предыдущей итерации.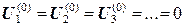 .
. , затем
, затем  по формуле (12.12).
по формуле (12.12).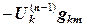 ненулевая, то выполняется следующая итерация. Невязка от предыдущей итерации оказывается в правой части уравнений (12.13), и мы ищем такую добавку к значениям неизвестных
ненулевая, то выполняется следующая итерация. Невязка от предыдущей итерации оказывается в правой части уравнений (12.13), и мы ищем такую добавку к значениям неизвестных  , чтобы она скомпенсировала невязку от предыдущей итерации. Суммируя предыдущее решение с этой добавкой, находим новое приближение по формуле (12.12).
, чтобы она скомпенсировала невязку от предыдущей итерации. Суммируя предыдущее решение с этой добавкой, находим новое приближение по формуле (12.12).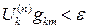 , либо приращения за шаг
, либо приращения за шаг  .
. , (12.16)
, (12.16)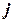 в нем присутствует удельная мощность теплового потока
в нем присутствует удельная мощность теплового потока 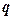 , вместо электропроводности
, вместо электропроводности  - коэффициент теплопроводности
- коэффициент теплопроводности 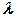 , а вместо напряженности (градиента) электрического поля
, а вместо напряженности (градиента) электрического поля  – градиент температур на границе
– градиент температур на границе 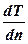 (
(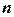 – вектор нормали к границе).
– вектор нормали к границе).
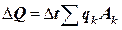 , (12.17)
, (12.17)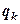 – удельная мощность потока теплоты через границу
– удельная мощность потока теплоты через границу  .
. в единице массы
в единице массы 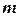 , которое называется теплосодержанием или энтальпией
, которое называется теплосодержанием или энтальпией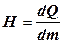 . (12.18)
. (12.18) , размерностью Дж/(кг·К).
, размерностью Дж/(кг·К).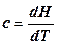 ; (12.19)
; (12.19) ;
;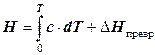 . (12.20)
. (12.20) , (12.21)
, (12.21) – накопление теплоты,
– накопление теплоты, 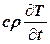 – изменение теплосодержания.
– изменение теплосодержания.
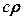 - теплоемкость
- теплоемкость , (12.26)
, (12.26)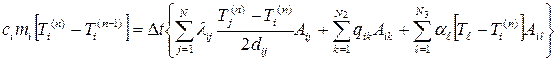 . (12.27)
. (12.27) . (12.28)
. (12.28) ; (12.29)
; (12.29) ; (12.30)
; (12.30) . (12.31)
. (12.31) необходимо исключить из системы уравнений (температуры в них уже известны). Одно из уравнений, с диагональным коэффициентом матрицы
необходимо исключить из системы уравнений (температуры в них уже известны). Одно из уравнений, с диагональным коэффициентом матрицы 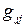 полностью исключается из системы (заменяется на
полностью исключается из системы (заменяется на 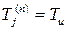 ). В остальных уравнениях из матрицы исключается столбец с коэффициентами
). В остальных уравнениях из матрицы исключается столбец с коэффициентами  , соответствующими узлу с температурой
, соответствующими узлу с температурой 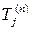 . Взамен него в правой части каждого из остальных уравнений появляется добавка
. Взамен него в правой части каждого из остальных уравнений появляется добавка  . Таким образом, с учетом всех граничных условий, в правой части имеем:
. Таким образом, с учетом всех граничных условий, в правой части имеем: . (12.32)
. (12.32)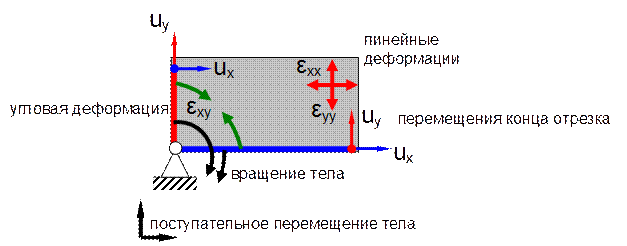
 ;
; .
.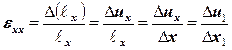 ;
; и т. д.
и т. д.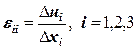 . (12.29)
. (12.29) .
.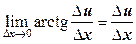 [рад];
[рад]; .
.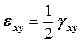 , получим единую формулу для малых линейных и угловых деформаций, которая включает в себя формулу (12.29), как частный случай:
, получим единую формулу для малых линейных и угловых деформаций, которая включает в себя формулу (12.29), как частный случай: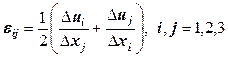 . (12.30)
. (12.30)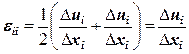
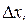 . Для бесконечно малой окрестности точки отношения превращаются в частные производные, поэтому деформации в точке тела
. Для бесконечно малой окрестности точки отношения превращаются в частные производные, поэтому деформации в точке тела . (12.31)
. (12.31) отрезка с учетом больших продольных и поперечных перемещений одного из его концов (рис. 12.15):
отрезка с учетом больших продольных и поперечных перемещений одного из его концов (рис. 12.15):
 не следует, что
не следует, что  и
и  ).
). . (12.32)
. (12.32)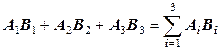 записывают как
записывают как 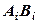 , пропуская знак суммы. О необходимости вычисления и суммирования произведений при всех значениях «слепого» индекса i сигнализирует его двукратное повторение в формуле. Традиционная запись последнего члена уравнения (12.32)
, пропуская знак суммы. О необходимости вычисления и суммирования произведений при всех значениях «слепого» индекса i сигнализирует его двукратное повторение в формуле. Традиционная запись последнего члена уравнения (12.32)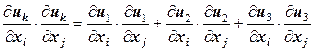 .
.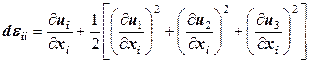 .
.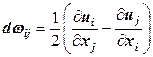 (12.33)
(12.33)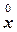 , называют деформацией Коши,
, называют деформацией Коши,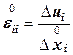 , (12.34)
, (12.34)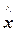 - деформацией Альманси:
- деформацией Альманси: ,
, . (12.35)
. (12.35)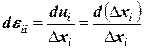 .
.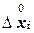 до
до  :
: . (12.36)
. (12.36)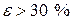 .
.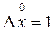 растянуть в два раза, то
растянуть в два раза, то  ,
, 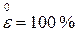 ,
,  , а
, а 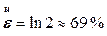 . Если тот же отрезок сжать в два раза, то
. Если тот же отрезок сжать в два раза, то 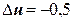 ,
,  ,
,  , а
, а  . Деформация Коши
. Деформация Коши  означает, что размер стал нулевым
означает, что размер стал нулевым 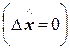 , а дальше размер меняет знак, «выворачивается наизнанку». Аналогично поведение деформации Альманси при
, а дальше размер меняет знак, «выворачивается наизнанку». Аналогично поведение деформации Альманси при  . Деформацию Генки называют истинной, поскольку она имеет одинаковые числовые значения при растяжении и сжатии в два раза и сохраняет физический смысл при любых значениях деформации:
. Деформацию Генки называют истинной, поскольку она имеет одинаковые числовые значения при растяжении и сжатии в два раза и сохраняет физический смысл при любых значениях деформации: 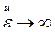 имеет место, когда тело вытягивается в длинную нить, а
имеет место, когда тело вытягивается в длинную нить, а 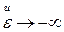 , когда тело расплющивается в тонкую пластину. Возможность пересчета любого из трех видов деформации в остальные показывает, что все они равноценны.
, когда тело расплющивается в тонкую пластину. Возможность пересчета любого из трех видов деформации в остальные показывает, что все они равноценны. . (12.37)
. (12.37) (12.38)
(12.38) – относительное изменение объема
– относительное изменение объема 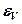 :
: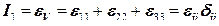 ,
, - символ Кронекера,
- символ Кронекера,  .
. . (12.39)
. (12.39)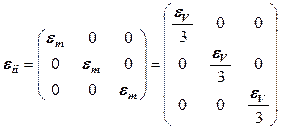 . (12.40)
. (12.40) характеризует только изменение формы тела, его шаровая составляющая нулевая:
характеризует только изменение формы тела, его шаровая составляющая нулевая: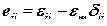 ; (12.41)
; (12.41)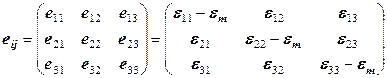 ; (12.42)
; (12.42)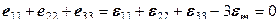 . (12.43)
. (12.43)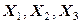 все угловые компоненты тензора становятся равными нулю и остаются только линейные деформации
все угловые компоненты тензора становятся равными нулю и остаются только линейные деформации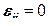 при
при 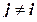 ,
, , (12.44)
, (12.44) . (12.45)
. (12.45)  переходят в линейные, и наоборот:
переходят в линейные, и наоборот:  (рис. 12.16), поскольку при взаимном повороте двух осей (при угловой деформации) изменяется расстояние между парой точек, лежащих на этих осях (происходит линейная деформация отрезка, соединяющего эту пару точек).
(рис. 12.16), поскольку при взаимном повороте двух осей (при угловой деформации) изменяется расстояние между парой точек, лежащих на этих осях (происходит линейная деформация отрезка, соединяющего эту пару точек).
 ;
;  . Любые комбинации из инвариантов также являются инвариантами.
. Любые комбинации из инвариантов также являются инвариантами.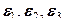 – это корни кубического уравнения
– это корни кубического уравнения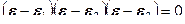 (12.46)
(12.46)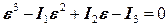 . (12.47)
. (12.47)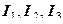 по компонентам произвольного тензора, например:
по компонентам произвольного тензора, например: ;
; . (12.48)
. (12.48) , то после деформации он превращается в эллипсоид, осями симметрии которого являются главные оси деформации, а длина осей эллипсоида составляет
, то после деформации он превращается в эллипсоид, осями симметрии которого являются главные оси деформации, а длина осей эллипсоида составляет  . Дальнейшую деформацию можно представить себе либо как растяжение и сдвиг этого эллипсоида (в результате каждый раз получается опять эллипсоид), либо как его вращение в пространстве с изменением длины главных осей.
. Дальнейшую деформацию можно представить себе либо как растяжение и сдвиг этого эллипсоида (в результате каждый раз получается опять эллипсоид), либо как его вращение в пространстве с изменением длины главных осей.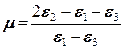 (12.49)
(12.49)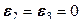 (осевое растяжение), то
(осевое растяжение), то  ; если
; если 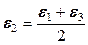 (кручение), то
(кручение), то 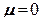 ; если
; если  (двухосное растяжение), то
(двухосное растяжение), то 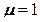 .
.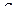 ; значение второго (интенсивности деформации) – радиус большого круга, значение третьего (параметра Лодэ
; значение второго (интенсивности деформации) – радиус большого круга, значение третьего (параметра Лодэ  ) - соотношение размеров малых кругов.
) - соотношение размеров малых кругов.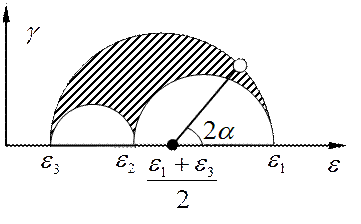
 – угол между главной осью и осью координат; заштрихована область возможных сочетания линейных и угловых деформаций при различной ориентации осей координат)
– угол между главной осью и осью координат; заштрихована область возможных сочетания линейных и угловых деформаций при различной ориентации осей координат) . (12.50)
. (12.50)
 .
.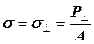 ,
,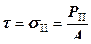 .
.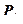 и
и 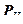 . Напряженное состояние в элементарном объеме характеризуют компоненты напряжения на трех секущих поверхностях, перпендикулярных осям координат. Силу, передаваемую через поверхность, можно разложить по осям координат и найти для каждого сечения три компоненты напряжения: нормальную и две касательных. Для обозначения компоненты используют два индекса, один из которых обозначает ось, нормальную к поверхности, а другой – ось, по которой действует составляющая силы. В тензорной записи оси обозначают номерами 1, 2 и 3, нормальные компоненты
. Напряженное состояние в элементарном объеме характеризуют компоненты напряжения на трех секущих поверхностях, перпендикулярных осям координат. Силу, передаваемую через поверхность, можно разложить по осям координат и найти для каждого сечения три компоненты напряжения: нормальную и две касательных. Для обозначения компоненты используют два индекса, один из которых обозначает ось, нормальную к поверхности, а другой – ось, по которой действует составляющая силы. В тензорной записи оси обозначают номерами 1, 2 и 3, нормальные компоненты  , а касательные компоненты
, а касательные компоненты  . Общая формула
. Общая формула


