
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение тождественности логических функцийСодержание книги Поиск на нашем сайте
Пример 7. Получить путем тождественных преобразований минимальную форму записи логической функции F1 и проверить, является ли она тождественной функции F2 (слайд 26).
Упростим функцию F1. Так как функция F1 задана аналитически, то будем производить упрощение по шагам:
1-й шаг
2-й шаг
3-й шаг
(по правилу склеивания для КНФ).
Таким образом, функция F1 тождественно равна функции F2, так как совпадают их минимальные формы.
Пример 8. Получить путем тождественных преобразований логической функции F1 ее минимальную форму записи и проверить, является ли она тождественной функции F2, определенной на данных наборах (слайд 27).
F2=1 на наборах (100), (101), (110).
1) Функция F2 определена таблично, запишем ее в СДНФ:
2) Упрощаем вторую скобку функции F1: ¾ ¾ __ __ __ __ X2X3+X1X3 = X2+X3+X1Х3 = Х2+Х3+Х1
Тогда
Таким образом, логическая функция F1, заданная аналитически, тождественна функции F2, заданной таблично. Пример 9. Получить путем тождественных преобразований логической функции F2 ее минимальную форму записи и проверить, является ли она тождественной функции F1, определенной на данных наборах (слайды 28-29).
F1=0 на наборах: (000), (010), (011), (100), (110), (111)
Так как F1=0 на 6 заданных наборах, то F1=1 на остальных наборах (001) и (101) (см. таблицу истинности F1):
Следовательно, нужно представить F1в СДНФ
Преобразуем F2:
Используя основные соотношения алгебры логики (АÙА=А), можно представить функцию F2 в виде:
Применяя вторую форму распределительного закона ко 2-ой и 4-ой скобкам и к 3-ей и 5-ой скобкам, получим следующее:
Применив вторую форму распределительного закона к 1-ой и 3-ей скобке, получим:
Таким образом, функции F1 и F2 тождественны.
Примечание: Логические функции тождественны, если совпадают их минимальные формы. Если минимальные формы не совпадают, то необходимо обе функции привести к любой совершенной форме (СДНФ или СКНФ), используя правила расширения, и сравнить совершенные формы. Если они совпадают, то функции тождественны.
Построение таблиц истинности
Пример 10. Получить таблицу истинности функции F2, заданной аналитически: Для построения таблиц истинности необходимо представить функцию в совершенной форме (СДНФ или СКНФ). Приведем функцию F2 к совершенной дизъюнктивной форме: 1) Упростим вторую скобку
2)
Применим правило расширения, чтобы получить СДНФ. Умножим X1X2 на
Эта функция является СДНФ и принимает значение 1 на наборах: 000 - 0 ö 111 – 7 ý = 1, и 0 на остальных наборах 0. 110 – 6 ø
Тогда таблица истинности будет выглядеть следующим образом:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.009 с.) |

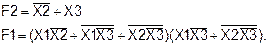
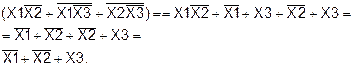
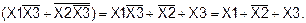
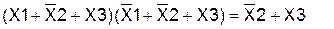
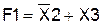 (полученный результат).
(полученный результат). (исходная функция).
(исходная функция).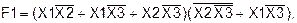
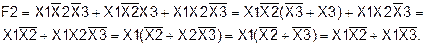
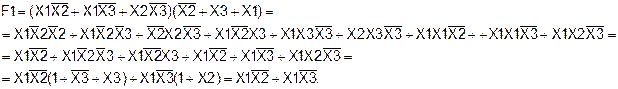
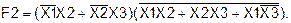
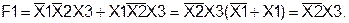

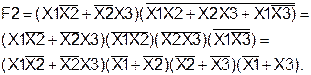
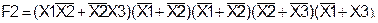
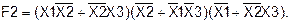
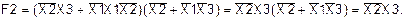
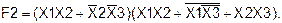 (слайды 30-31).
(слайды 30-31).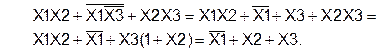
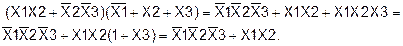
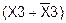 и получим:
и получим:



