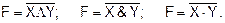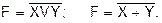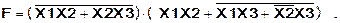Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные логические функцииСодержание книги Поиск на нашем сайте
Логические функции, зависящие от одной или двух переменных, называются элементарными. К основным логическим функциям относятся следующие элементарные функции: отрицание; логическое умножение; отрицание от логического умножения; логическое сложение; отрицание от логического сложения; равнозначность; отрицание равнозначности. Функция отрицания - это логическая функция от одного аргумента, которая принимает значение 1, если аргумент равен 0, и принимает значение 0, если аргумент равен 1, и называется отрицанием (инверсией) или логической функцией НЕ (слайд 3). Запись логической функции НЕ –
Функцией логического умножения n аргументов называется логическая функция, которая принимает значение 1 только в том случае, когда все аргументы равны 1, а 0– во всех остальных случаях (слайд 4). Функцию логического умножения называют также конъюнкцией или функцией И. Элементарная функция логического умножения зависит от двух аргументов и описывается следующей таблицей истинности:
Запись логической функции И: F=XΛY; F=X&Y; F=X×Y, где знаки «Λ», «&», «.» – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны. Функцией логического сложения n аргументов называется логическая функция, которая принимает значение 0только в том случае, когда все аргументы равны 0 (т.е. при наборе n нулей), и 1 во всех остальных случаях (т.е. когда хотя бы один аргумент равен 1) (слайд 5). Функцию логического сложения называют также дизъюнкцией или логической функцией ИЛИ. Элементарная дизъюнкция зависит от двух аргументов и описывается следующей таблицей истинности:
Запись логической функции ИЛИ: F=XVY; F=X+Y, где знаки «V», «+» обозначают операцию логического сложения. Функция отрицания от логического умножения принимает значение 0, когда все аргументы равны 1, и 1 – во всех остальных случаях (слайд 6):
Запись логической функции: Функция отрицания от логического сложения принимает значение 1, когда все аргументы равны 0, и значение 0 – во всех остальных случаях (слайд 7):
Запись логической функции: В сложных выражениях с использованием логических операций И, ИЛИ, НЕ сначала выполняются операции отрицания НЕ, затем операции конъюнкции И и, в последнюю очередь, операции дизъюнкции ИЛИ. Для того, чтобы изменить указанную последовательность выполнения операций, в выражениях следует использовать скобки. Например:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

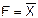 , где черта над переменной – признак инверсии. Логическая функция НЕ от одного аргумента описывается следующей таблицей истинности:
, где черта над переменной – признак инверсии. Логическая функция НЕ от одного аргумента описывается следующей таблицей истинности: