Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы и правила упрощения логических функцийСодержание книги Поиск на нашем сайте
Соотношения, законы и правила алгебры логики
В алгебре логики имеют место следующие соотношения и действуют следующие законы (слайд 15). Соотношения
Законы отрицания (инверсии)
а) отрицание конъюнкции
Отрицание от конъюнкции равно дизъюнкции отрицаний.
б) отрицание дизъюнкции
Отрицание от дизъюнкции равно конъюнкции отрицаний. Переместительный закон
Логические функции И и ИЛИ подчиняются переместительному закону:
Сочетательный закон
Логические функции И и ИЛИ подчиняются сочетательному закону:
Дистрибутивный (распределительный) закон
Непосредственной проверкой можно убедиться, что операции логического сложения и логического умножения подчиняются дистрибутивному (распределительному) закону: одинаковые переменные в конъюнкциях и дизъюнкциях можно выносить за скобку (слайд 16). а)дистрибутивный закон умножения по отношению к сложению имеет такой же вид, как и для алгебраического сложения и умножения, например:
б)дистрибутивный закон сложения по отношению к умножению является специфичным для алгебры логики и не имеет аналогов в обычной алгебре:
Непосредственно из дистрибутивного закона вытекают следующие правила, которые используются при преобразовании функций, при их минимизации, т.е. приведении их к виду с наименьшим числом конъюнкций минимально возможного ранга, после которого функция не поддается дальнейшему упрощению. Из первой формы дистрибутивного закона вытекают следующие правила (слайд 17): Правило склеивания для ДНФ
а) (для 2 переменных)
б) (для 3 переменных)
Это правило позволяет заменить два члена, имеющие общую часть и аргумент с инверсией в одном члене и без инверсии в другом члене, одним общим членом, т.е. произвести склеивание.
Правило поглощения для ДНФ
а) (для 2 переменных)
XVXY = X.
б) (для 3 переменных)
XVX Λ YVX Λ Y Λ Z = X.
Это правило позволяет заменить 2 или больше члена, один из которых входит в другой (конъюнкция) в качестве сомножителя, одним этим членом, т.е. произвести “поглощение” члена конъюнкции общим членом. Из второй формы дистрибутивного закона вытекает правило свертки (слайд 18).
Правило свертки для ДНФ a) или
b)
Это правило позволяет упростить один из членов дизъюнктивной нормальной формы. Аналогичные формулы существуют для преобразования конъюнктивных нормальных форм (слайд 18).
Правило склеивания для КНФ
Правило поглощения для КНФ
Правило свертки для КНФ
Пример 5. Пусть логическая функция задана аналитически:
Требуется упростить функцию (получить ее минимальную форму) (слайды 19-20).
· Преобразуем член с инверсией:
· Раскроем скобки:
(конъюнкция · Преобразуем член с конъюнкцией:
· Подставляем преобразованные выражения в исходную формулу:
Это нормальная дизъюнктивная форма. Применяя к ней правила склеивания и поглощения, можно ее упростить:
· к 1-му и 2-му членам применим правило склеивания:
· к 3-му и 5-му членам применим правило поглощения:
Получим:
Результат
|
|||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.009 с.) |

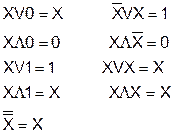


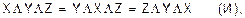
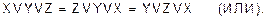
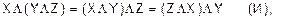
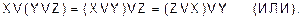
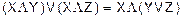 (распределение конъюнкции по дизъюнкции);
(распределение конъюнкции по дизъюнкции);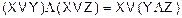 (распределение дизъюнкции по конъюнкции).
(распределение дизъюнкции по конъюнкции).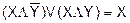 .
.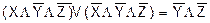

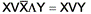
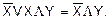
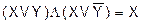
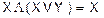
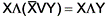
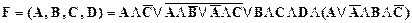
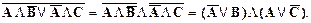
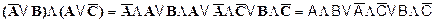
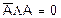 )
)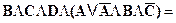 { раскрываем скобки } =
{ раскрываем скобки } =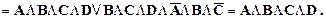
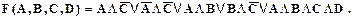
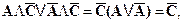
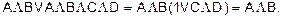
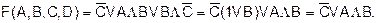
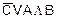 не подлежит дальнейшему преобразованию (упрощению). Следовательно, минимальная форма исходной функции:
не подлежит дальнейшему преобразованию (упрощению). Следовательно, минимальная форма исходной функции: