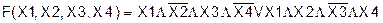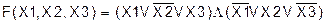Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произвольные логические функции – днф и кнфСодержание книги Поиск на нашем сайте
Предположим, что произвольная логическая функция n аргументов задана единственным набором аргументов, при котором эта функция принимает значение 1 (слайд 8). Составим конъюнкцию (логическую функцию И) от всех n аргументов: аргументы, которые в указанном наборе равны 0, возьмем со знаком инверсии, а аргументы, равные 1 в указанном наборе, без знака инверсии, так как согласно определению конъюнкции, чтобы логическая функция И принимала значение 1, необходимо, чтобы все аргументы были равны 1.
Пример 1. Задана логическая функция от 4 аргументов Х1, Х2, Х3, Х4, которая принимает значение 1 при наборе Х1=0, Х2=1, Х3=1, Х4=0 и 0 - при всех остальных наборах. Составим конъюнкцию для этой функции:
Предположим, что произвольная логическая функция n аргументов задана единственным набором аргументов, при котором эта функция принимает значение 0 (слайд 9). Составим дизъюнкцию (логическую функцию ИЛИ) от всех n аргументов следующим образом: аргументы, равные 0 в заданном наборе, возьмем без знака инверсии, а аргументы, равные в заданном наборе 1, со знаком инверсии, так как согласно определению дизъюнкции, чтобы логическая функция ИЛИ принимала значение 0, необходимо, чтобы все аргументы были равны 0.
Пример 2. Задана логическая функция от четырех аргументов Х1, Х2, Х3, Х4, которая принимает значение 0 при следующем наборе Х1=0, Х2=0, Х3=1, Х4=1 и 1 при всех остальных наборах. Составим дизъюнкцию для этой функции:
Произвольная логическая функция, заданная перечислением всех наборов аргументов, при которых она принимает значение 1, определяется следующим образом: для каждого из этих наборов составляется конъюнкция, а затем образуется дизъюнкция всех этих конъюнкций (слайд 10).
Пример 3. Предположим, что функция 4 аргументов Х1, Х2, Х3, Х4 принимает значение 1 при наборах:
Х1=1 Х2=0 Х3=1 Х4=0 Х1=0 Х2=0 Х3=1 Х4=1 Х1=1 Х2=1 Х3=0 Х4=1
и 0 на всех остальных наборах. Тогда функция, сформированная таким образом, будет иметь вид:
Для любого из перечисленных наборов эта функциябудет представлять собой дизъюнкцию одной 1 и остальных 0, т.е. будет равна 1, а на остальных наборах будет представлять собой дизъюнкцию одних нулей, т.е. будет равна 0. Произвольная логическая функция, заданная перечислением всех наборов аргументов, при которых она принимает значение 0, определяется следующим образом: для каждого из этих наборов составляется дизъюнкция, а затем образуется конъюнкция всех этих дизъюнкций (слайд 11).
Пример 4. Предположим, что задана функция от 3 аргументов F(Х1,Х2,Х3 ), которая принимает значение 0 при наборах:
Х1=0 Х2=1 Х3=1 Х1=1 Х2=0 Х3=0 Х1=0 Х2=0 Х3=0
и 1 при всех остальных наборах. Тогда функция, сформированная таким образом, будет иметь вид:
Для любого из перечисленных наборов функция F(Х1, Х2, Х3) будет представлять собой конъюнкцию одного нуля и остальных единиц, то есть будет равна 0, а на остальных наборах будет представлять конъюнкцию одних единиц, то есть равна 1. Из вышеизложенного можно сделать следующий вывод (слайд 12): произвольная логическая функция от n аргументов может быть выражена через логические функции И, ИЛИ, НЕ (конъюнкцию, дизъюнкцию, отрицание). Логические функции, представляющие собой дизъюнкции отдельных членов, каждый из которых есть в свою очередь некоторая функция, содержащая только конъюнкции и инверсии, называются логическими функциями дизъюнктивной формы (слайд 13). Логические функции дизъюнктивной формы, в которых инверсия применяется лишь непосредственно к аргументам, например, Если каждый член дизъюнктивной нормальной функции от n аргументов содержит все n аргументов, часть из которых со знаком инверсии, а часть без него, то функция называется совершенной (СДНФ). Например, функция
представляет собой СДНФ. Каждый член такой формы обращается в 1 лишь при некотором единственном наборе аргументов, а число членов равно числу разных наборов, обращающих функцию в 1. В несовершенных дизъюнктивных нормальных функциях от n аргументов некоторые члены содержат количество аргументов меньшее, чем n. Такие члены принимают значение 1 при нескольких наборах аргументов. Потому и число членов в несовершенных формах меньше, чем число членов в совершенных формах этих же функций. Логические функции, представляющие собой конъюнкции отдельных членов, каждый из которых есть в свою очередь некоторая функция, содержащая только дизъюнкции и инверсии, называются логическими функциями конъюнктивной формы (слайд 14).
Логические функции конъюнктивной формы, в которых инверсия применяется лишь непосредственно к аргументам, но не к более сложным функциям, называются нормальными конъюнктивными функциями. Если каждый член конъюнктивной нормальной функции от n аргументов содержит все n аргументов, часть из которых со знаком инверсии, а часть без него, то функция называется совершенной (СКНФ). Например, функция
представляет собой СКНФ. Каждый член такой формы обращается в 0 лишь при некотором единственном наборе аргументов, а число членов равно числу разных наборов, обращающих функцию в 0.
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.182.195 (0.007 с.) |

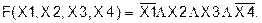
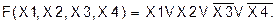
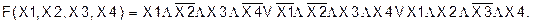
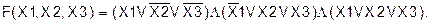
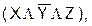 но не к более сложным функциям, как, например
но не к более сложным функциям, как, например 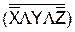 , называются нормальными дизъюнктивными функциями.
, называются нормальными дизъюнктивными функциями.