Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площадей по методу трапецииСодержание книги
Поиск на нашем сайте
Из рисунка Рисунок 19 видно, что площадь фигуры можно рассчитать путем сложения площадей фигур, получившихся при рассечении ее параллельными прямыми. Рассмотрим, что же представляет собой эти фигуры, например, выделенная зеленым цветом на рисунке Рисунок 19. Так как две стороны ее – параллельные прямые, а часть кривой можно с достаточной точностью заменить прямой линией, то получается, что это – трапеция, у которой у i и у i +1 – основания трапеции, а Δ l – ее высота. Тогда площадь этой трапеции определяется по формуле:
(11) Таким образом, можно рассчитать площади каждой части фигуры, так как каждая из них – трапеция, и тогда площадь всей фигуры будет равна S = (12) Или
Полученное выражение и есть формула трапеций, которую можно записать, используя значок суммы, следующим образом:
(13)
Теперь обратимся к теоретическому чертежу.
§ 9. Определение площади шпангоута и площади ватерлинии На теоретическом чертеже площади шпангоутов можно рассчитать, используя, например, проекцию «Корпус», на которой видны поперечные сечения судна.
Преобразуя формулу (13) применительно к данному чертежу, получим формулу для вычисления площади погруженной части шпангоута:
(14) где ω – площадь погруженной части шпангоута в м²; Т – осадка судна в м; п – количество промежутков между ватерлиниями (число ватерлиний минус 1); у – полуординаты, снятые с теоретического чертежа. Высота элементарной трапеции при расчете площади шпангоута определяется расстоянием между ватерлиниями, которое равно Т/п. Цифра 2 появилась в формуле (14) потому, что на теоретическом чертеже изображены половинки шпангоутов, так как они симметричны. Поэтому и координата у i называется полуординатой. Мы же должны рассчитать площадь всего шпангоута.
Для определения площади ватерлинии используют проекцию «Полуширота» теоретического чертежа, так как только там видна плоскость ватерлинии.
На рисунке Рисунок 21 видно, что плоскость ватерлинии уже расчерчена параллельными прямыми теоретического чертежа. Воспользовавшись формулой (13) можно получить формулу для расчета площади ватерлинии по теоретическому чертежу:
(15)
где S – площадь ватерлинии в м²; Δ L – теоретическая шпация, которая определяется делением длины по грузовой ватерлинии на количество шпангоутов минус 1: Δ L = L / n; у - полуординаты. Цифра 2 появляется, потому что на теоретическом чертеже изображается половина ватерлинии.
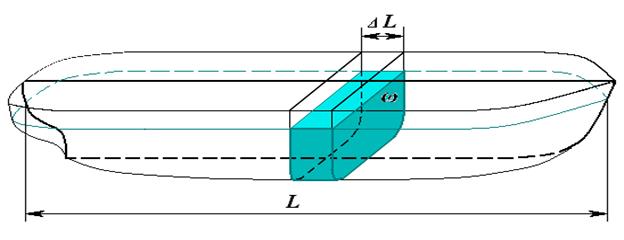
§ 10. Вычисление объемов (водоизмещения) Если тело разделить равноотстоящими параллельными плоскостями на несколько частей, то объем тела можно вычислить путем сложения объемов его составляющих. Объем отдельной части корпуса (Рисунок22) вычисляется как произведение полусуммы площадей оснований на высоту. Площади оснований данной фигуры – площади погруженной части шпангоутов, ограничивающих эту фигуру. Высотой будет расстояние между шпангоутами Δ L, то есть – теоретическая шпация. Проведя преобразования, подобные приведенным выше, получим формулу для вычисления водоизмещения по площадям шпангоутов:
(16)
где V – водоизмещение в м³; Δ L – теоретическая шпация; ω – площадь погруженной части шпангоута в м².
(17)
где V – водоизмещение в м³; Т – осадка судна в м; п – количество промежутков между ватерлиниями (число ватерлиний минус 1); S – площадь ватерлинии в м². Точность расчета повышается с увеличением количества делений, но при этом резко возрастает громоздкость расчетов.
ТЕОРИЯ КОРАБЛЯ Глава 1. ПЛАВУЧЕСТЬ
§ 11. Условия плавучести и равновесия судна Плавучестью называется способность судна держаться на воде (плавать) в определенном положении относительно поверхности воды. Что позволяет судну не только держаться на воде, но и перевозить пассажиров и грузы? Если мы возьмем металлическую пластину и опусти ее в воду, то она, естественно, утонет. Но если мы придадим этой же пластине форму, например, лодочки, то она, возможно, останется на поверхности воды. Что же произошло? Ведь вес пластины остался прежним, но она обрела плавучесть, т.е. способность держаться на воде? Все дело в том, что мы изменили форму пластины, а с ней и силу, которая держит ее на воде. Еще древнегреческий мыслитель Архимед, живший в 3 веке до нашей эры, сформулировал закон, который позволяет не только объяснить, почему суда не тонут, но и рассчитать ту силу, которая держит тела на поверхности воды. Закон Архимеда гласит: · На тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной телом жидкости.
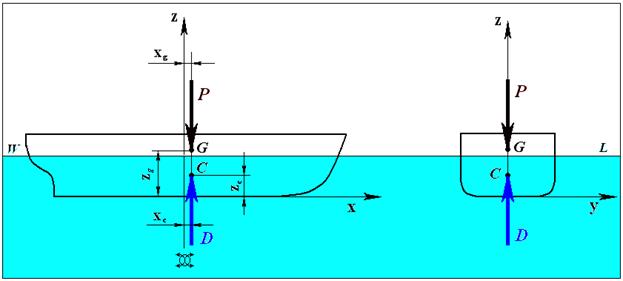
Иными словами, для того, чтобы определить выталкивающую силу, достаточно знать удельный вес жидкости и объем вытесненной воды. В случае с пластиной мы не изменили ее вес, не изменили ее собственный объем, а изменили объем вытесняемой воды. Если судно находится на спокойной воде, на него действуют силы веса самого судна и его составляющих, в том числе груза, и силы поддержания. Вес судна распределен по всей длине судна неравномерно, все зависит от расположения деталей и устройств судна, а также от места расположения перевозимого груза. Силы поддержания тоже распределены по длине судна, а не направлены в одну точку. Расчеты навигационных качеств судна в теории корабля основываются на том, что действие распределенной нагрузки заменяется равнодействующей, приложенной в точке. Величина этой равнодействующей равна суммарной нагрузке. Равнодействующая сил веса Р направлена вертикально вниз и приложена в точку G, которая называется центром тяжести. Центр тяжести судна – это точка абсолютного равновесия судна. Ее положение зависит от величины веса судна и грузов, а также от расположения этих весов по судну. То есть, положение этой точки не постоянное, а меняется в процессе эксплуатации судна. Силы веса уравновешивается силами поддержания, равнодействующая которых D приложена в точку C, которая называется центром величины, и направлена вертикально вверх. Центр величины судна определяется, как геометрический центр тяжести погруженной части корпуса судна, поскольку силы поддержания определяются по закону Архимеда объемом погруженной части корпуса судна, которая называется водоизмещением. И, следовательно, положение этой точки зависит от формы погруженной части корпуса. Судно будет находиться на поверхности воды в равновесии, если силы веса и поддержания будут равны, противоположно направлены по одной прямой, т.е., будут выполнены следующие условия:
Р = D; x g = x c; y g = y c = 0 (18)
Эти выражения и представляют собой условия равновесия плавающего судна.
Первая строка является математической записью закона плавучести, который гласит: · Всякое тело, плавающее на поверхности воды, весит столько, сколько весит вытесненная им вода
Если обозначить удельный вес воды через γ, то закон Архимеда можно записать следующим образом:
(19) где D – сила поддержания или весовое водоизмещение судна в тоннах; V – водоизмещение судна в м³; γ – удельный вес воды в т/м³. При расчетах плавучести принимают: для пресной воды………………………….1,000 т/м³. для морской воды………………………….1,025 т/м³. Это выражение (19) иногда называют уравнением плавучести. Вес плавающего судна, или его весовое водоизмещение, представляет собой сумму весов конструкций, механизмов, оборудования, перевозимого груза, топлива и т.д. Часть весов зависит от водоизмещения, другая часть – нет.
§ 12. Весовые и объемные характеристики судна К основным характеристикам судна относятся: · водоизмещение, · грузоподъемность, · грузовместимость. Водоизмещение судна в свою очередь, бывает объемным и весовым. Объемным водоизмещением называется объем погруженной части корпуса судна,что соответствует и объему вытесненной судном воды. Обозначается объемное водоизмещение V и измеряется в кубических метрах (м³). Весовым водоизмещением называется вес судна или вес вытесненной судном воды. Весовое водоизмещение обозначается буквой D и измеряется в тоннах (т).
Рисунок 24 Дедвейт и собственный вес порожнего судна 1 – полезный груз, 2 – дедвейт, 3 – полное водоизмещение, 4 – грузовая ватерлиния, 5 – водоизмещение порожнего судна, 6 – ватерлиния порожнего судна
Во время эксплуатации судна водоизмещение постоянно меняется, но при этом не может быть менее водоизмещения судна порожнём, но и не может быть более полного водоизмещения судна. Основными видами водоизмещения гражданских судов являются: · водоизмещение порожнего судна Dпор, · полное водоизмещение Dпол. Разность между полным водоизмещением и водоизмещением в порожнем состоянии называется дедвейтом или полной грузоподъемностью судна: DW = D пол - D пор Он складывается из полезного груза (чистой грузоподъемности), подлежащего перевозке, и прочих переменных грузов. К полезному грузу относятся также пассажиры с багажом и необходимые для них запасы провизии и воды. Чистая грузоподъемность получается после вычитания из полной грузоподъемности (дедвейта) переменных грузов.
К переменным грузам относятся: · топливо, · вода для питания котлов, · смазочное масло, · экипаж с багажом, · необходимые для него вода и провизия, · расходные материалы В число постоянных весов, образующих водоизмещение порожнего судна, входят следующие веса: · вес корпуса и надстройки – Р к; · машинная установка – Р м; · судовые системы и устройства; · электрооборудование и связь; · часть снабжения. Для оценки степени использования водоизмещения судна по назначению служат так называемые коэффициенты использования (утилизации) по дедвейту: η дв = (20) где DW – дедвейт судна; D – весовое водоизмещение судна; и коэффициент использования по чистой грузоподъемности: η чг = (21_) где Р чг – чистая грузоподъемность судна. Коэффициент использования по дедвейту для данного судна является величиной постоянной и характеризует само судно, коэффициент использования по чистой грузоподъемности во многом зависит от действий экипажа. Четкое планирование рейсов, рациональные запасы топлива и питьевой воды, продуманная загрузка судна способствуют увеличению этого коэффициента и в конечном итоге – повышению эффективности работы судна.
§ 13. Строевая по шпангоутам. Строевая по ватерлиниям.
Строевая по шпангоутам – это диаграмма, показывающая, как изменяется по длине судна площадь погруженной части шпангоута ω. Строевую по шпангоутам вычерчивают по точкам, откладывая в соответствующем масштабе вычисленные по теоретическому чертежу площади погруженной части каждого шпангоута по вертикали вверх на соответствующем шпангоуте. Строевая по шпангоутам обладает следующими свойствами: 1. Если рассчитать площадь строевой по шпангоутам, а для этого можно воспользоваться известным нам методом трапеций, так как поверхность ее расчерчена параллельными прямыми, мы получим водоизмещение судна: 2. Коэффициент полноты строевой по шпангоутам рассчитывается путем деления площади строевой, которая равна водоизмещению V, на площадь описанного прямоугольника, стороны которого 3. Центр тяжести строевой определяет положение центра величины судна, то есть абсцисса геометрического центра тяжести строевой по шпангоутам равна абсциссе х с центра величины судна. 4. Сама строевая по шпангоутам показывает распределение водоизмещения по длине судна, а, следовательно, и распределение силы поддержания, которая определяется через водоизмещение судна. 5. По строевой по шпангоутам можно определить площадь погруженной части шпангоута в любом сечении судна.
Если аналогично построить диаграмму зависимости площади ватерлинии S от осадки судна Т, то мы получим строевую по ватерлиниям. На вертикальной оси наносят положение ватерлиний судна и от них по горизонтали откладывают в соответствующем масштабе площади ватерлиний, рассчитанные по теоретическому чертежу.
1. Площадь строевой по ватерлиниям равна водоизмещению судна. Если рассчитать по методу трапеций площадь фигуры, образованной строевой по ватерлиниям, получим 2. Коэффициент полноты строевой по ватерлиниям равен коэффициенту вертикальной полноты судна 3. Центр тяжести строевой по ватерлиниям определяет положение центра величины судна по осадке z c. 4. Строевая по ватерлиниям показывает распределение водоизмещения судна по осадке. 5. По строевой по ватерлиниям легко определить площадь любого сечения судна по ватерлиниям.
§ 14. Кривая водоизмещения. Грузовой размер. Грузовая шкала. Масштаб Бонжана.
Кривая водоизмещения
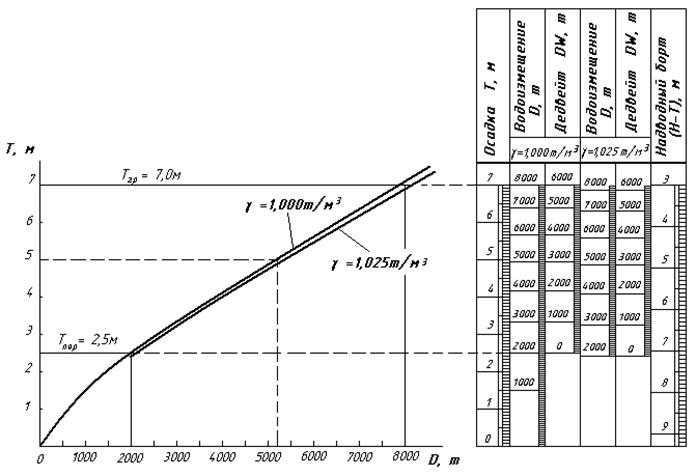
Кривая водоизмещения позволяет определить: -фактическое водоизмещение судна при данной осадке; -осадку при данном водоизмещении; -изменение осадки при приеме и снятии известного количества груза; -количество принятого или снятого груза по известному изменению средней осадки. Кривую водоизмещения строят по точкам, откладывая по горизонтальной оси рассчитанные значения водоизмещения судна для данной конкретной осадки. Но на практике чаще пользуются не объемными характеристиками, а весовыми. Для их опре деления пользуются кривой, которая называется грузовой размер. Грузовым размером называется кривая, показывающая зависимость весового водоизмещения от средней осадки судна. Очевидно, что для пресной воды кривая водоизмещения и грузовой размер совпадают. Для судов, плавающих как в пресной воде, так и в соленой на чертеже грузового размера наносят две кривые: одна для пресной воды, другая – для соленой. И еще, так как грузовой размер определяет фактически вес судна, то, учитывая, что судно имеет минимальный вес, ниже которого оно весить не может, - вес судна порожнем, то отсчет осадок на грузовом размере начинается с осадки, соответствующей весу судна порожнем, то есть нижняя часть кривой отбрасывается. Пользоваться грузовым размером на практике несколько затруднительно, так как даже небольшое отклонение от параллельности системе координат приводит к значительной погрешности в определении данных. Поэтому для удобства грузовых расчетов строят специальную номограмму, называемую грузовой шкалой. Грузовая шкала представляет собой таблицу с вертикальными колонками, в которых разбиты шкалы для осадок, водоизмещения, дедвейта и надводного борта. Шкалы дедвейта и водоизмещения есть как для пресной воды, так и для соленой. Иногда грузовую шкалу дополняют еще шкалами для осадки в футах и числа тонн груза, меняющих осадку на 1 сантиметр. Грузовая шкала позволяет более просто и с большей точностью решать все перечисленные задачи и является официальным документом, по которому судят о количестве погруженного и выгруженного груза, что очень важно, особенно при перевозке массового груза.
Масштабом Бонжана пользуются следующим образом. Определившись с осадкой носом и кормой судна, отмечают их на соответствующих шкалах и проводят прямую через эти точки. Фактически мы получаем ватерлинию судна. Эта ватерлиния пересекает все шпангоуты, а точки ее пересечения с вертикальными прямыми каждого шпангоута - осадка судна на данном шпангоуте. Далее проводя горизонтальную прямую из точки пересечения, можно определить площадь погруженной части шпангоута ω i. Таким образом можно определить все площади шпангоутов, а затем рассчитать водоизмещение судна:
где ω i – площадь погруженной части шпангоута; Δ L – теоретическая шпация.
§ 15. Изменение осадки судна при приеме или расходовании малого груза Малым принято считать груз, вес которого не превышает 10% веса судна. При приеме груза вес судна увеличивается, что приводит к увеличению водоизмещения судна, а, следовательно, и средней осадки судна. Для определения величины изменения средней осадки судна определим одну и ту же величину разными способами. Мы будем определять приращение водоизмещения Δ V по закону Архимеда и геометрически. Итак, определимся со всеми величинами до и после приема груза весом р. Принимаем сразу, что в случае приема груза вес его будет положительный, если груз расходуется, вес его будет отрицательный, т.е. в этом случае мы принимаем отрицательный груз.
Таблица 1
Определим, как изменится водоизмещение Δ V. По закону Архимеда – формула (19)
D = γ V После приема груза по аналогии
D + p = γ (V + ΔV) (22) Отсюда определим Δ V, преобразовав формулу (22):
(23) Но, изменив формулу (19) - закон Архимеда, получим
(24)
Подставим (24) в (23) и получаем следующее выражение:
(25)
Теперь определим изменение водоизмещения судна, исходя из геометрии судна. Учитывая, что груз малый, можно предположить, что площадь ватерлинии судна при погружении не изменилась. Следовательно, объем части корпуса, вошедшей в воду, определяем, как объем цилиндра, основание которого – площадь ватерлинии, а высота – изменение осадки ΔT. Объем такой фигуры равен произведению площади основания на высоту, т.е.
ΔV = S ΔT, (26) где S – площадь действующей ватерлинии, которая определяется по формуле S = αLB (4):
S = αLB, где α – коэффициент полноты ватерлинии, L – длина судна, B – ширина судна.
Приравняв Δ V, полученное разными путями по формулам (25) и (26), получим следующее выражение:
откуда
(27) )
Т' = Т + ΔТ (28) При решении судоводителями задач, связанных с изменениями средней осадки судна при приеме и снятии малого груза на практике пользуются величиной q, которая определяет массу груза, которая меняет осадку данного судна на 1см. Зная величину груза, меняющего осадку на 1см, легко определить изменение осадки в сантиметрах:
(29)
Или в метрах соответственно:
(30)
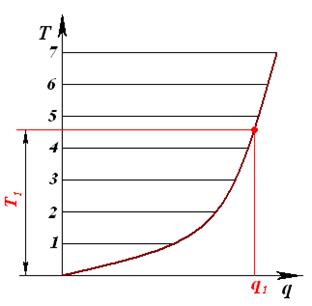
Из приведенных формул (27) и (29) видно, что q прямо пропорционально площади ватерлинии S. Поэтому, применив к строевой по ватерлиниям масштаб в виде величины 0,01γ, можно построить кривую числа тонн на см осадки. По этой кривой, зная осадку судна, можно определить величину q, а, следовательно, рассчитать возможное изменение осадки при приеме малого груза.
§ 16. Изменение осадки судна при переходе из пресной воды в соленую и наоборот Суда смешанного река-море плавания постоянно осуществляют переходы из морских районов в речные и обратно. При таких переходах при неизменном весе самого судна меняется удельный вес воды, а, следовательно, изменится осадка самого судна. Для упрощения расчетов будем пользоваться следующей схемой: судно переходит из водоема 1 в водоем 2. При этом параметры судна будут следующими:
Таблица 2
Как и в предыдущем параграфе, будем определять величину изменения водоизмещения Δ V двумя разными способами: используя закон Архимеда и геометрически. При переходе из одного водоема в другой водоизмещение изменится на величину, которую можно определить, как разницу между водоизмещением во втором и в первом водоемах:
Δ V = V 2 - V 1 (31) В свою очередь, используя формулу (24), получим:
(32)
(33) Подставим (32) и (33) в (31) и получим:
(34)
Геометрически, используя формулу (26) из предыдущего параграфа, объем, на который изменится водоизмещение, будет равен
ΔV = S ΔT.
Приравнивая правые части этих двух выражений, получим следующее:
(35)
Или
(36)
где ΔТ – изменение осадки при переходе из одного водоема в другой, D – весовое водоизмещение судна (вес судна), S – площадь действующей ватерлинии, γ 1 - удельный вес воды в 1 водоеме, γ 2 – удельный вес воды во 2 водоеме. Если разделить в выражении (36) D на γ 1, то получим водоизмещение судна в 1 водоеме V 1, которое можно вычислить, используя коэффициент общей полноты водоизмещения и главные размерения судна: V 1 = δ L В Т В свою очередь площадь ватерлинии может быть определена через коэффициент полноты ватерлинии: S = α L В Учитывая, что D = γV, и, подставляя приведенные значения в формулу (36), получим следующее:
(37)
где δ – коэффициент общей полноты водоизмещения судна, α – коэффициент полноты ватерлинии, Т 1 – первоначальная осадка судна. Знак ΔТ зависит от направления перехода, что видно из данной формулы. Если судно переходит из пресной воды в соленую (γ 1 < γ 2), то величина ΔТ будет отрицательной, а новая осадка будет меньше первоначальной. Если же судно переходит из морской воды в пресную (γ 1 > γ 2), то величина ΔТ будет положительной, и новая осадка будет больше первоначальной.
§ 17. Запас плавучести. До сих пор мы рассматривали и рассчитывали объем только погруженной части корпуса – водоизмещения. Но, как известно, весь корпус – это водонепроницаемая часть судна, а значит, судно не потеряет плавучести до тех пор, пока корпус не уйдет в воду. Тем не менее, предел погружения судна – грузовая ватерлиния. Почему? Просто непогруженная часть корпуса является как бы «аварийным запасом» на случай, если судно будет вынуждено увеличить свое водоизмещение, например, при приеме воды в случае получения пробоины. Поэтому надводная часть корпуса так и называется – запас плавучести. Запас плавучести судна можно определить по следующей формуле:
V ЗП = S КВЛ (Н – Т)(1 + k), (38) где V ЗП – запас плавучести; S КВЛ – площадь грузовой ватерлинии; Н – высота борта; T – осадка судна; k – коэффициент, учитывающий развал бортов, седловатость палубы, наличие водонепроницаемых надстроек и рубок. Степень непотопляемости судна тем выше, чем выше относительный запас плавучести судна, который определяется как отношение запаса плавучести к расчетному водоизмещению судна. Относительный запас плавучести зависит от типа судна и составляет для танкеров 15-25%, для сухогрузов – 25-50%, для пассажирских судов – 80% и более. Очевидно, что запас плавучести судна зависит от величины надводного борта судна, который определяется, как (Н – T). Чем больше высота надводного борта судна, тем больше запас плавучести. Высота надводного борта – мера запаса плавучести судна, величина которой устанавливается для всех судов Правилами Речного Регистра. Необходимым условием назначения высоты надводного борта является удовлетворение требований правил Регистра к прочности, остойчивости и непотопляемости судна. Речной Регистр, исходя из этого, назначает судну в зависимости от его размеров, назначения и района плавания, минимальный надводный борт, который фиксируется путем нанесения на борту грузовой марки.
§ 18. Грузовая марка.
o палубной линии; o диска (круга) Плимсоля; o гребенок осадок. Верхняя кромка горизонтальной линии, проходящей через центр круга Плимсоля, соответствует линии предельной осадки при плавании в районе, соответствующем указанному классу судна, основной символ которого ставится у этой линии.
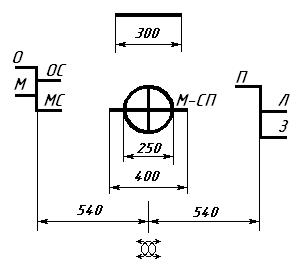
Рисунок 33 Грузовая марка судов смешанного (река-море) плавания
Глава 2. ОСТОЙЧИВОСТЬ
§ 19. Основные понятия и определения
Остойчивостью называется способность судна, отклоненного внешними силами, возвращаться в исходное положение после п
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 2402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.116.77 (0.016 с.) |


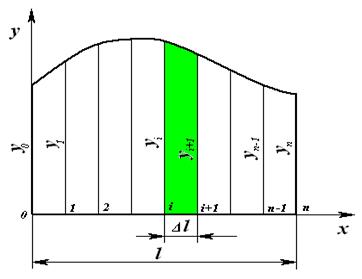 Для определения площади криволинейной фигуры, изображенной на рисунке, воспользуемся методом трапеций. Для этого разобьем данную фигуру на части параллельными прямыми. Чтобы провести эти прямые, разделим одну из сторон l на несколько равных частей Δ l и проведем через точки параллельные прямые. Отрезки параллельных прямых – ординаты у согласно присоединенной системе координат, а индексы у – номер точки.
Для определения площади криволинейной фигуры, изображенной на рисунке, воспользуемся методом трапеций. Для этого разобьем данную фигуру на части параллельными прямыми. Чтобы провести эти прямые, разделим одну из сторон l на несколько равных частей Δ l и проведем через точки параллельные прямые. Отрезки параллельных прямых – ординаты у согласно присоединенной системе координат, а индексы у – номер точки.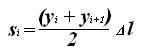 .
.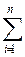 s i = s 1 + s 2 + … + s n-1 + s n
s i = s 1 + s 2 + … + s n-1 + s n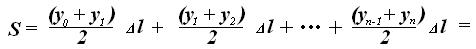
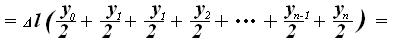
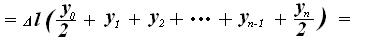
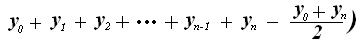
 .
.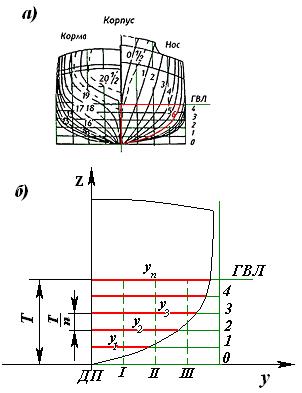
 Рассмотрим один из них, например, шестой шпангоут. На рисунке Рисунок 20- а его контур выделен красным цветом. На рисунке Рисунок 20- б изображен тот же шестой шпангоут, но уже отдельно. Можно заметить, что плоскость шпангоута уже рассечена параллельными прямыми – это ватерлинии, параллельные оси 0у и батоксы, параллельные оси 0 z. Можно рассчитывать, используя как ватерлинии, так и батоксы, но ватерлинии чаще расположены, и расчеты с ними будут более точными, поэтому расчет площади погруженной части шпангоута целесообразней вести, снимая ординаты у с ватерлиний теоретического чертежа.
Рассмотрим один из них, например, шестой шпангоут. На рисунке Рисунок 20- а его контур выделен красным цветом. На рисунке Рисунок 20- б изображен тот же шестой шпангоут, но уже отдельно. Можно заметить, что плоскость шпангоута уже рассечена параллельными прямыми – это ватерлинии, параллельные оси 0у и батоксы, параллельные оси 0 z. Можно рассчитывать, используя как ватерлинии, так и батоксы, но ватерлинии чаще расположены, и расчеты с ними будут более точными, поэтому расчет площади погруженной части шпангоута целесообразней вести, снимая ординаты у с ватерлиний теоретического чертежа.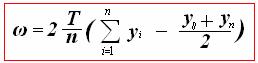


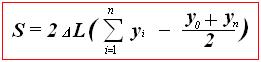 ,
, ,
,
 Если использовать в качестве сечений площади ватерлиний, можно получить еще одну формулу для расчета водоизмещения:
Если использовать в качестве сечений площади ватерлиний, можно получить еще одну формулу для расчета водоизмещения: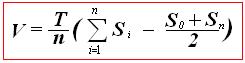 ,
,

 D = γ V
D = γ V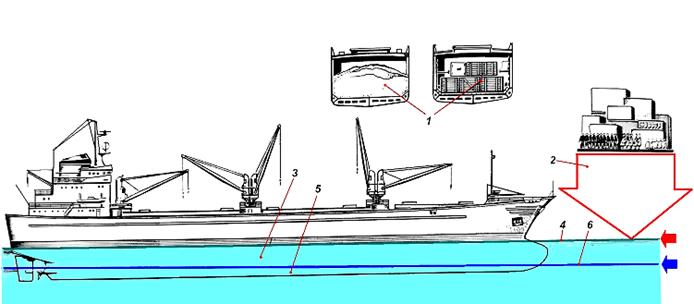
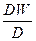 ,
,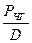 ,
,
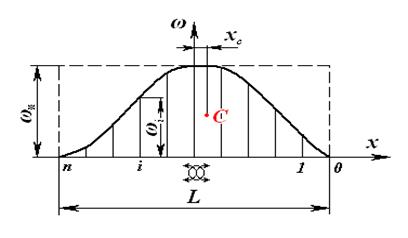 Так как плавучесть – способность судна держаться на воде – зависит от величины силы поддержания, а та в свою очередь определяется по объему погруженной части корпуса судна – водоизмещению, можно водоизмещение считать мерой плавучести судна.
Так как плавучесть – способность судна держаться на воде – зависит от величины силы поддержания, а та в свою очередь определяется по объему погруженной части корпуса судна – водоизмещению, можно водоизмещение считать мерой плавучести судна.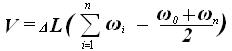 .
.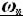 и Т, и равен коэффициенту продольной полноты судна
и Т, и равен коэффициенту продольной полноты судна 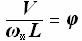

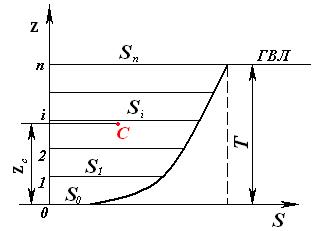 Строевая по ватерлиниям обладает следующими свойствами:
Строевая по ватерлиниям обладает следующими свойствами: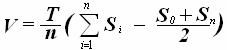
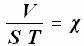 .
. Рисунок 27
Рисунок 27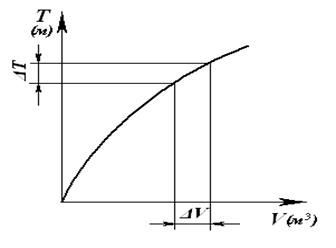 Используя строевую по ватерлиниям, а именно, рассчитав с ее помощью водоизмещение суд на при различных осадках, можно построить кривую, показывающую зависимость водоизмещения судна от его осадки. Такая кривая называется кривой водоизмещения.
Используя строевую по ватерлиниям, а именно, рассчитав с ее помощью водоизмещение суд на при различных осадках, можно построить кривую, показывающую зависимость водоизмещения судна от его осадки. Такая кривая называется кривой водоизмещения. 

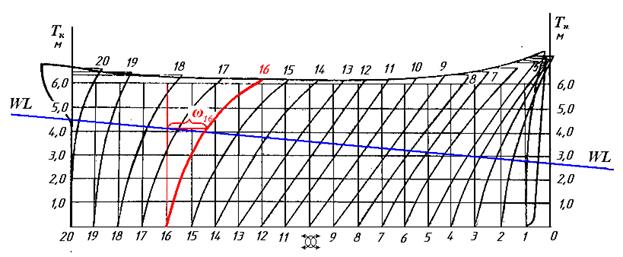 Если судно имеет большой дифферент, то для определения его водоизмещения пользуются специальной диаграммой, которая называется масштаб Бонжана. Масштаб Бонжана представляет собой совокупность кривых, которые показывают изменение площади каждого шпангоута в зависимости от осадки на данном шпангоуте. Кроме этих кривых масштаб Бонжана имеет еще две шкалы – осадки носом на нулевом шпангоуте и осадки кормой на последнем.
Если судно имеет большой дифферент, то для определения его водоизмещения пользуются специальной диаграммой, которая называется масштаб Бонжана. Масштаб Бонжана представляет собой совокупность кривых, которые показывают изменение площади каждого шпангоута в зависимости от осадки на данном шпангоуте. Кроме этих кривых масштаб Бонжана имеет еще две шкалы – осадки носом на нулевом шпангоуте и осадки кормой на последнем.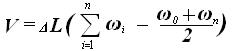 ,
, 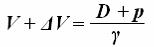 ,
,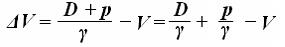
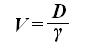
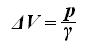
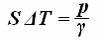 ,
,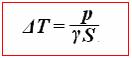

 Новая осадка судна будет:
Новая осадка судна будет: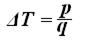
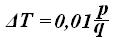
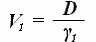
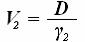
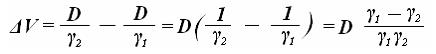
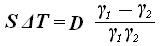
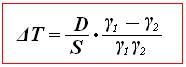
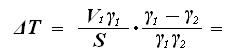
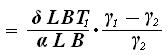
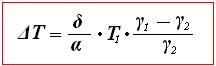
 Грузовая марка – это специальный знак, наносимый на бортах судна в районе мидель-шпангоута, состоящий из
Грузовая марка – это специальный знак, наносимый на бортах судна в районе мидель-шпангоута, состоящий из
 Если судно предназначено совершать рейсы в водных бассейнах различных разрядов, то от конца горизонтальной линии круга в носовой части марки следует нанести вертикальную черту и дополнительные линии предельных осадок – так называемые «гребенки». Каждая горизонтальная линия гребенки определяет высоту надводного борта данного судна в водоеме определенного класса, символ которого стоит у этой черты. Получается, что символ, стоящий у горизонтальной черты круга Плимсоля означает класс судна, все остальные – класс водоема. Рассмотрим грузовую марку, изображенную на рисунке 32- г. Эта марка соответствует судну класса «О», и высота надводного борта его при плавании в водоеме разряда «О» определяется расстоянием от палубной линии до линии середины круга. При плавании в водоеме более низкого разряда это судно может уменьшить высоту надводного борта от палубной линии до линий «Л» или «Р». При плавании в водоеме разряда «М» судно обязано увеличить высоту надводного борта, то есть его грузовая линия как бы опускается. Так же требуется увеличить надводный борт судну класса «М» при нахождении в водоеме «МС», и так далее.
Если судно предназначено совершать рейсы в водных бассейнах различных разрядов, то от конца горизонтальной линии круга в носовой части марки следует нанести вертикальную черту и дополнительные линии предельных осадок – так называемые «гребенки». Каждая горизонтальная линия гребенки определяет высоту надводного борта данного судна в водоеме определенного класса, символ которого стоит у этой черты. Получается, что символ, стоящий у горизонтальной черты круга Плимсоля означает класс судна, все остальные – класс водоема. Рассмотрим грузовую марку, изображенную на рисунке 32- г. Эта марка соответствует судну класса «О», и высота надводного борта его при плавании в водоеме разряда «О» определяется расстоянием от палубной линии до линии середины круга. При плавании в водоеме более низкого разряда это судно может уменьшить высоту надводного борта от палубной линии до линий «Л» или «Р». При плавании в водоеме разряда «М» судно обязано увеличить высоту надводного борта, то есть его грузовая линия как бы опускается. Так же требуется увеличить надводный борт судну класса «М» при нахождении в водоеме «МС», и так далее. Грузовые марки судов смешанного (река – море) плавания (рисунок 33) отличаются от грузовых марок судов внутреннего плавания тем, что в круге Плимсоля появляется вертикальная черта такая же, как и у морских судов прибрежного плавания. Кроме того, у них не одна, а две «гребенки». Кормовая гребенка определяет высоту надводного борта для различных водоемов, как и у судов внутреннего плавания. Носовая – фактически учитывает то обстоятельство, что суда смешанного плавания эксплуатируются круглый год. Но ветро-волновые характеристики водоемов летом и зимой несколько различны, и требования к высоте надводного борта разные. Отсюда и при определении понятия «грузовая ватерлиния» оговаривается следующее: грузовая ватерлиния соответствует полной загрузке судна летом. Зимой высоту надводного борта необходимо увеличить. Именно это и определяют буквы «Л» и «З». Буква «П» означает – пресная вода. Как мы помним, при переходе судна из соленой воды в пресную осадка судна при том же весе увеличивается.
Грузовые марки судов смешанного (река – море) плавания (рисунок 33) отличаются от грузовых марок судов внутреннего плавания тем, что в круге Плимсоля появляется вертикальная черта такая же, как и у морских судов прибрежного плавания. Кроме того, у них не одна, а две «гребенки». Кормовая гребенка определяет высоту надводного борта для различных водоемов, как и у судов внутреннего плавания. Носовая – фактически учитывает то обстоятельство, что суда смешанного плавания эксплуатируются круглый год. Но ветро-волновые характеристики водоемов летом и зимой несколько различны, и требования к высоте надводного борта разные. Отсюда и при определении понятия «грузовая ватерлиния» оговаривается следующее: грузовая ватерлиния соответствует полной загрузке судна летом. Зимой высоту надводного борта необходимо увеличить. Именно это и определяют буквы «Л» и «З». Буква «П» означает – пресная вода. Как мы помним, при переходе судна из соленой воды в пресную осадка судна при том же весе увеличивается.