
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часть 2. Геометрическое моделирование.
Представление пространственных форм. Каркасная модель. Полигональные сетки. Во многих приложениях машинной графики возникает потребность в представлении трехмерных форм. Совокупность отрезков не является адекватным описанием объекта, поскольку отрезки сами по себе не определяют поверхностей. В то же время информация о поверхностях необходима для проведения вычислений, связанных со стиранием скрытых частей изображения, для определения объемов и т. д. Таким образом, мы приходим к выводу, что для описания трехмерных форм необходимы поверхности – примитивы более высокого уровня, чем отрезки. Каркасная модель Каркасная модель — модель объекта в трёхмерной графике, представляющая собой совокупность вершин и рёбер, которая определяет форму отображаемого многогранного объекта. Полигональная сетка
Полигональная сетка представляет собой совокупность ребер, вершин и многоугольников. 2 .Параметрические кривые, параметр, непрерывность. В параметрическом виде каждая координата точки кривой представлена как функция одного параметра. Значение параметра задает координатный вектор точки на кривой. Для двумерной кривой с параметром
Тогда векторное представление точки на кривой:
Чтобы получить непараметрическую форму, нужно исключить Параметрическая форма позволяет представить замкнутые и многозначные кривые. Производная, т. е. касательный вектор, есть
где ' обозначает дифференцирование по параметру. Наклон кривой,
Отметим, что при Так как точка на параметрической кривой определяется только значением параметра, эта форма не зависит от выбора системы координат. Конечные точки и длина кривой определяются диапазоном изменения параметра. Часто бывает удобно нормализовать параметр на интересующем отрезке кривой к Самое простое параметрическое представление у прямой. Для двух векторов положения
Так как
|
|||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.46.36 (0.005 с.) |

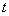 координаты точки равны:
координаты точки равны: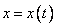 ,
, .
.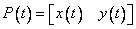 .
.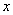 и
и 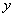 .
.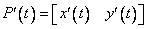 ,
,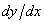 , равен
, равен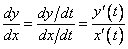 .
.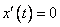 наклон бесконечен. Параметрическое представление не вызывает в этом случае вычислительных трудностей, достаточно приравнять нулю одну компоненту касательного вектора.
наклон бесконечен. Параметрическое представление не вызывает в этом случае вычислительных трудностей, достаточно приравнять нулю одну компоненту касательного вектора.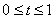 . Осенезависимость параметрической кривой позволяет с легкостью проводить с ней аффинные преобразования, рассмотренные в гл. 2 и 3.
. Осенезависимость параметрической кривой позволяет с легкостью проводить с ней аффинные преобразования, рассмотренные в гл. 2 и 3.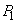 и
и  параметрический вид отрезка прямой между ними такой:
параметрический вид отрезка прямой между ними такой: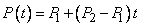 ,
, 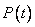 это вектор, у каждой его составляющей есть параметрическое представление
это вектор, у каждой его составляющей есть параметрическое представление  и
и 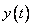 между
между 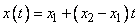 ,
,  .
.


