Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы математической логикиСодержание книги
Поиск на нашем сайте
Для анализа сложных событий вводятся понятия логической суммы (дизъюнкции) и логического произведения (конъюнкции) событий. Суммой событий А и В называют событие С:
C = A˅B, (1.18)
где ˅ - знак логического суммирования (дизъюнкции). Событие считается свершившимся, если произошло хотя бы одно из событий А и В или оба вместе. Произведением событий А и В называют событие С:
С = А˄В, (1.19)
где ˄ - знак логического произведения (конъюнкции). Событие С считается свершившимся, если произошло каждое из событий А и В. Совокупность нескольких событий называется группой событий. Полная группа событий - совокупность событий, хотя бы одно из которых должно произойти. Например, событие А (отказ изделия) и противоположное событие Вероятность суммы двух событий А и В:
Р(А˅B) = Р(А) + Р(В) - Р(А˄В), (1.20)
где Р(А˄В) - вероятность совместного появления событий А и В. Для несовместных событий А и В, то
Р(А˅B) = Р(А) + Р(В). (1.21)
Вероятность суммы трёх событий А, В и С:
P(A˅B˅С) = Р(А) + Р(В) + Р(С) – Р(А˄В) - Р(В˄С) - Р(С˄А) + + Р(А˄В˄С). (1.22)
Для несовместных событий А, В и С:
Р(А˅B˅С) = Р(А) + Р(В) + P(С). (1.23)
Если события А, В и С образуют полную группу событий, т.е. хотя бы одно из них обязательно осуществится, то
P(A˅B˅С) = 1. (1.24)
Для полной группы несовместных событий из условий (1.22) и (1.23) следует:
P(A) + P(B) + P(С) = 1. (1.25)
В частности, для суммы вероятностей противоположных событий
Р(А) + Р(
Величина Р(В|А) называется условной вероятностью события В (при условии, что событие А произошло), тогда
Р(А˄В) = Р(А) · Р(В|А) (1.27) или Р(А˄В) = Р(В) · Р(А|В) (1.28)
В теории вероятности более приняты сокращённые обозначения логического произведения событий в виде обычного алгебраического произведения, тогда равенства (1.25) и (1.26) запишутся так:
Р(АВ) = Р(А) · Р(В|А) = Р(В) · Р(А|В). (1.29)
Понятие условной вероятности приводит к условию независимости событий. Событие В считается независящим от события А, если
Р(В|А) = Р(В). (1.30)
Несовместные события всегда зависимые, тогда как совместные события могут быть зависимыми или независимыми. Для независимых событий:
Р(АВ) = Р(А)Р(В). (1.31)
Из соотношений (1.28) и (1.30) вытекает условие Р(А|В) = Р(А), т.е. независимость событий - понятие взаимное. Для группы из трёх событий:
P(ABС) = Р(А)Р(В|А)Р(С|АВ) = Р(В)Р(А|В)Р(С|ВА) = = P(С)P(A|С)P(B|AС), (1.31)
а для независимых событий:
P(ABС) = P(A)P(B)P(С). (1.32)
Пример. Вероятность безотказной работы двух трансформаторов под нагрузкой Р = 0,9. Какова вероятность того, что не произойдёт одновременный отказ обоих трансформаторов? Решение. Принимаем: безотказная работа первого трансформатора - событие А, второго трансформатора - событие В. Тогда безотказная работа одного из трансформаторов или обоих вместе есть сумма событий A˅В. Вероятность отсутствия одновременного отказа обоих трансформаторов (сумма событий А и В) при условии независимости отказов определяем по формуле (1.20):
Р(А˅B) = 0,9 + 0,9 - 0,9 · 0,9 = 0,99.
ТЕМА 2. ОСНОВНЫЕ ПОНЯТИЯ И ПОКАЗАТЕЛИ ТЕОРИИ НАДЕЖНОСТИ Надежность как наука
Надежность характеризует качество технического средства. Качество – совокупность свойств, определяющих пригодность изделия к использованию по назначению и его потребительские свойства. Надежность – комплексное свойство технического объекта, которое состоит в его способности выполнять заданные функции, сохраняя свои основные характеристики в установленных пределах. Понятие надежности включает в себя безотказность, долговечность, ремонтопригодность и сохранность. Предмет надежности – изучение причин, вызывающих отказы объектов, определение закономерностей, которым они подчиняются, разработка способов количественного измерения надежности, методов расчета и испытаний, разработка путей и средств повышения надежности. Объектом исследования надежности как науки является то или иное техническое средство: отдельная деталь, узел машины, агрегат, машина в целом, изделие и др. Различают общую теорию надежности и прикладные теории надежности. Общая теория надежности имеет три составляющие: 1. Математическая теория надежности. Определяет математические закономерности, которым подчиняются отказы и методы количественного измерения надежности, а также инженерные расчеты показателей надежности. 2. Статистическая теория надежности. Обработка статистической информации о надежности. Статистические характеристики надежности и закономерности отказов. 3. Физическая теория надежности. Исследование физико-химических процессов, физических причин отказов, влияния старения и прочности материалов на надежность. Прикладные теории надежности разрабатываются в конкретной области техники применительно к объектам этой области. Например, существует теория надежности систем управления, теория надежности электронных устройств, теория надежности машин и др. Надежность связана с эффективностью (например, с экономической эффективностью) техники. Недостаточная надежность технического средства имеет следствием: – снижение производительности из-за простоев вследствие поломок; – снижение качества результатов использования технического средства из-за ухудшения его технических характеристик вследствие неисправностей; – затраты на ремонты технического средства; – потеря регулярности получения результата (например, снижение регулярности перевозок для транспортных средств); – снижение уровня безопасности использования технического средства.
Основные понятия надежности
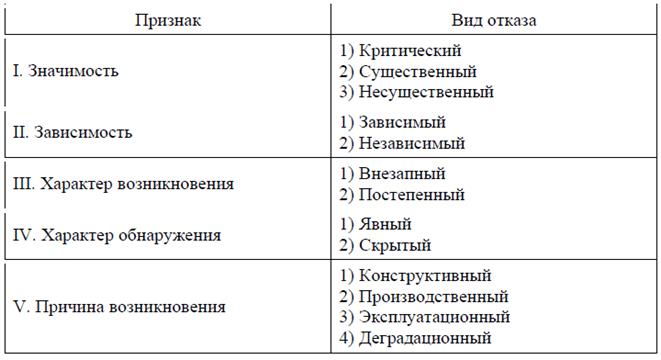
Надежность использует понятие объекта. Объект характеризуется качеством. Надежность является составляющим показателем качества объекта. Чем выше надежность объекта, тем выше его качество. В процессе эксплуатации объект может находиться в одном из следующих состояний (рисунок 2.1): 1) Исправное состояние – состояние объекта, при котором он соответствует всем требованиям нормативно-технической и (или) конструкторской документации. 2) Неисправное состояние – состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно-технической и (или) конструкторской документации. 3) Работоспособное состояние – состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствует требованиям нормативно-технической и (или) конструкторской документации. 4) Неработоспособное состояние – состояние объекта, при котором значение хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям нормативно-технической и (или) конструкторской документации. Различают неисправности, не приводящие к отказам (нарушение лакокрасочного покрытия, износ протектора колеса), и неисправности, ведущие к возникновению отказа (трещина металлоконструкции рамы, изгиб лопасти вентилятора системы охлаждения двигателя). Частным случаем неработоспособного состояния является предельное состояние. Предельное состояние – состояние, при котором дальнейшая эксплуатация объекта недопустима или нецелесообразна, либо восстановление работоспособного состояния невозможно или нецелесообразно. Переход объекта в предельное состояние влечет за собой временное или окончательное прекращение эксплуатации объекта, то есть объект должен быть выведен из эксплуатации, направлен в ремонт или списан. Критерии предельного состояния устанавливают в нормативно-технической документации. Повреждение – это событие, заключающееся в нарушении исправного состояния объекта при сохранении работоспособного состояния. Отказ – это событие, заключающееся в нарушении работоспособного состояния объекта. Восстановление (ремонт) – возвращение объекту работоспособного состояния. Критерии повреждений и отказов устанавливают в нормативно-технической и (или) конструкторской документации.
1 – повреждение; 2 – отказ; 3 – ремонт; 4 – переход в предельное состояние из-за наличия критического дефекта; I – критический дефект; II – значительный дефект; III – малозначительный дефект Рисунок 2.1 - Схема основных технических состояний
Классификация отказов приведена в таблице 2.1.
Таблица 2.1 – Классификация отказов
Зависимый отказ – отказ, обусловленный другими отказами. Внезапный отказ – характеризуется резким изменением одного или нескольких заданных параметров объекта. Примером внезапного отказа является нарушение работоспособности системы зажигания или системы питания двигателя. Постепенный отказ – характеризуется постепенным изменением одного или нескольких заданных параметров объекта. Характерным примером постепенного отказа является нарушение работоспособности тормозов в результате износа фрикционных элементов. Явный отказ – отказ, обнаруживаемый визуально или штатными методами и средствами контроля и диагностирования при подготовке объекта к применению или в процессе его применения по назначению. Скрытый отказ – отказ, не обнаруживаемый визуально или штатными методами и средствами контроля и диагностирования, но выявляемый при проведении технического обслуживания или специальными методами диагностики. В зависимости от способа устранения отказа все объекты разделяют на ремонтируемые (восстанавливаемые) и неремонтируемые (невосстанавливаемые). К ремонтируемым относят объекты, которые при возникновении отказа ремонтируют и после восстановления работоспособности снова вводят в эксплуатацию. Неремонтируемые объекты (элементы) после возникновения отказа заменяют. К таким элементам относятся большинство асбестовых и резинотехнических изделий (тормозные накладки, накладки дисков сцепления, прокладки, манжеты), некоторые электротехнические изделия (лампы, предохранители, свечи зажигания), быстроизнашивающиеся и обеспечивающие безопасность эксплуатации детали (вкладыши и пальцы шарниров рулевых тяг, втулки шкворневых соединений). К числу неремонтируемых элементов машин относят также подшипники качения, оси, пальцы, крепежные детали. Восстановление перечисленных элементов экономически нецелесообразно, так как затраты на ремонт достаточно велики, а обеспечиваемая при этом долговечность значительно ниже, чем у новых деталей.
|
||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.113 (0.009 с.) |

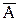 (безотказность изделия) составляют полную группу событий, так как изделие не может одновременно находиться в неисправном и исправном состоянии. Группа событий считается несовместной, если любые два события этой группы не могут произойти одновременно. Например, если признак (измеряемый параметр) разбит на три диагностических интервала (обрыв, короткое замыкание и нормальное состояние обмотки электрической машины), а события А1, А2, А3 означают появление признака в соответствующем интервале, то указанные события - несовместные. События А и
(безотказность изделия) составляют полную группу событий, так как изделие не может одновременно находиться в неисправном и исправном состоянии. Группа событий считается несовместной, если любые два события этой группы не могут произойти одновременно. Например, если признак (измеряемый параметр) разбит на три диагностических интервала (обрыв, короткое замыкание и нормальное состояние обмотки электрической машины), а события А1, А2, А3 означают появление признака в соответствующем интервале, то указанные события - несовместные. События А и 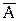 ) = 1. (1.26)
) = 1. (1.26)