
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики законов распределенияСодержание книги
Поиск на нашем сайте
В практике эксплуатации машин часто встречаются явления и процессы, представляющие собой случайные события, случайные величины и случайные функции (случайные процессы). Для получения обоснованных и оптимальных управленческих решений необходимо знать их законы распределения и их числовые характеристики. Между частными значениями случайной величины и вероятностями их появления существует определенная зависимость, которая называется законом распределения данной случайной величины - соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Для характеристики закона распределения случайной величины используются интегральные и дифференциальные функции. Закон распределения является исчерпывающей характеристикой случайной величины и может задаваться в виде таблицы, графика или формулы, например, в виде плотности распределения. Например: 1) Нормальное распределение. Плотность распределения (частота отказов) при нормальном законе определяется по формуле:
где х – значение случайной величины Х; σ – среднеквадратическое отклонение случайной величины Х. 2) Экспоненциальное распределение. Плотность распределения (частота отказов) при экспоненциальном законе определяется по формуле:
где λ – интенсивность случайной величины Х. 3) Распределение Вейбулла. Плотность распределения (частота отказов) при распределении Вейбулла определяется по формуле:
где λ – параметр масштаба; α – параметр формы. Законы распределения случайных величин описываются с помощью числовых характеристик. К основным числовым характеристикам можно отнести: 1) среднеарифметическое значение; 2) математическое ожидание; 3) размах; 4) дисперcию; 5) среднеквадратическое отклонение (СКО); 6) коэффициент вариации. Среднеарифметическое значение
Математическим ожиданием М(Х) случайной величины X называется сумма произведений всех ее возможных значений на их вероятности:
При достаточном количестве измерений (испытаний) выполняется условие:
Размах R случайной величины X – разность между наибольшим и наименьшим значениями величины:
R = xmax – xmin. (1.12) Дисперсией (рассеянием) D(X) случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Т.е. с учетом (1.10) получаем:
или
СКО случайной величины X называется квадратный корень из дисперсии:
Коэффициент вариации V случайной величины X – отношение СКО к среднему значению:
V = σ /
|
||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.75.218 (0.009 с.) |

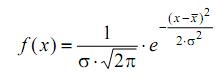 , (1.6)
, (1.6) - среднее значение случайной величины Х;
- среднее значение случайной величины Х;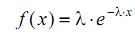 , (1.7)
, (1.7)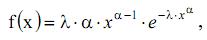 (1.8)
(1.8)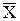 случайной величины Х – отношение суммы всех значений величины на общее число значений:
случайной величины Х – отношение суммы всех значений величины на общее число значений: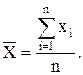 (1.9)
(1.9)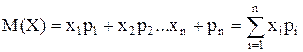 (1.10)
(1.10) (1.11)
(1.11) . (1.13)
. (1.13)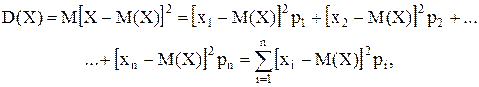 (1.14)
(1.14)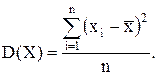 (1.15)
(1.15)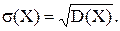 (1.16)
(1.16)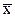 . (1.17)
. (1.17)


