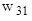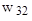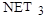Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизационная задача по обучению нейронной сети.Содержание книги
Поиск на нашем сайте
Обучение нейронных сетей является одной из основных областей применения генетических алгоритмов. Для построения и обучения нейронной сети зададим набор примеров, который представляет собой совокупность векторов вида Исходными данными для решения задачи являются количество входных и выходных нейронов; набор обучающих примеров. Требуется найти следующие характеристики нейронной сети: количество скрытых слоев; количество нейронов в каждом скрытом слое; значения весов всех входов для каждого скрытого и выходного нейрона; функции активации для каждого скрытого и выходного нейрона. Очевидно, что целевой функцией в данной задаче будет максимальное значение Таким образом, задача обучения нейронной сети сводится к задаче поиска оптимального решения. Следует заметить, что даже для простейших нейронных сетей эта задача является многомерной и крайне сложной. Цель найти нейронную сеть, удовлетворяющую условию Как правило, генетические алгоритмы используются на различных этапах построения и обучения сети в качестве основного или вспомогательного средства. Генетический алгоритм может использоваться на первом этапе работы для поиска общих параметров нейронной сети: количества скрытых слоев и нейронов. Также генетический алгоритм может использоваться на заключительном этапе работы для поиска всех значений весов нейронной сети и функций активации. Причем функции активации, как правило, выбираются из ограниченного набора, а еще чаще подбирается не сама формула функции активации, а один или несколько ее параметров. Для упрощения возьмем небольшую сеть прямого распространения (рис. 46) и построим для нее обучающий алгоритм. Сеть состоит из шести нейронов: трех входных, двух скрытых и одного выходного.
Рис. 46 Нейронная сеть. Используем сигмоидальную функцию качестве функции активации
где k – число примеров; Для останова работы генетического алгоритма можно указать число поколений, а можно задать условие на значение целевой функции. Например, остановить работу алгоритма, когда значение целевой функции Таблица 8 Структура кода.
Рассмотренный процесс показывает, насколько сложной является задача построения и обучения нейросети как с точки зрения ее размерности, так и с точки зрения ее вычислительной сложности. Тем не менее, генетические алгоритмы представляют один из эффективных и изящных путей ее решения.
Выводы по лекции. Эволюционные вычисления, в том числе и генетические алгоритмы, представляют собой подход к решению задачи поиска лучшего решения, а не четко определенный алгоритм. Для решения конкретной задачи, помимо ее формализации, формулировки генотипа и фенотипа, требуется создавать и конкретный генетический алгоритм. Для этого задают значения размера популяции, вероятности мутации, описывают процесс работы операторов отбора, скрещивания, мутации и редукции, что и было показано в рассмотренных примерах. Однако может оказаться, что алгоритм, успешно решающий одну задачу, совершенно не подходит для решения другой. Создание генетических алгоритмов, эффективно решающих как можно большее число задач, является предметом проводимых в настоящее время исследований.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.152 (0.006 с.) |

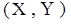 , где
, где 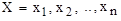 - значения всех входов нейронной сети, a
- значения всех входов нейронной сети, a 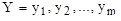 - значения всех выходов нейронной сети, которые должны получаться в процессе ее работы. Структура эталонных векторов задает одновременно количество входных и выходных нейронов, то есть в данном случае n и m соответственно. Целью обучения нейронной сети является достижение такой ситуации, когда при подаче на вход сети любого вектора X из набора примеров на ее выходе получается выходной вектор
- значения всех выходов нейронной сети, которые должны получаться в процессе ее работы. Структура эталонных векторов задает одновременно количество входных и выходных нейронов, то есть в данном случае n и m соответственно. Целью обучения нейронной сети является достижение такой ситуации, когда при подаче на вход сети любого вектора X из набора примеров на ее выходе получается выходной вектор 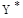 , отличающийся от эталонного вектора Y не более чем на заданную заранее и вычисляемую определенным образом величину
, отличающийся от эталонного вектора Y не более чем на заданную заранее и вычисляемую определенным образом величину 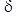 .
.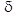 , полученное среди всех векторов
, полученное среди всех векторов 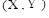 набора примеров. Подбирая значения характеристик нейронной сети и вычисляя каждый раз значение
набора примеров. Подбирая значения характеристик нейронной сети и вычисляя каждый раз значение 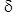 , можно найти такое значение
, можно найти такое значение 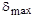 , которое требуется. Чем меньше значение
, которое требуется. Чем меньше значение 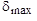 , тем качественнее будет построена нейронная сеть.
, тем качественнее будет построена нейронная сеть.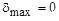 , для реальных задач недостижима и обычно не ставится. Поэтому поиск оптимального решения превращается в поиск лучшего решения, где с успехом можно применить генетический алгоритм.
, для реальных задач недостижима и обычно не ставится. Поэтому поиск оптимального решения превращается в поиск лучшего решения, где с успехом можно применить генетический алгоритм.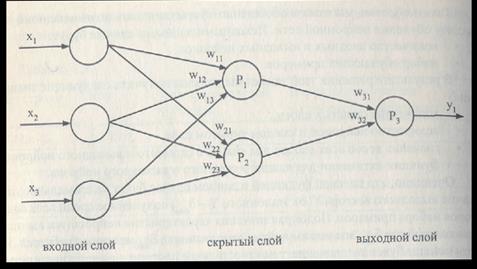
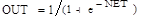 , а для вычисления значения целевой функции выражение
, а для вычисления значения целевой функции выражение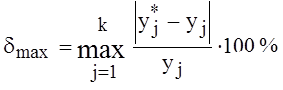 ,
,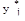 - значение выхода нейронной сети для j –го примера;
- значение выхода нейронной сети для j –го примера; 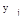 - эталонное значение выхода нейронной сети для j – го примера.
- эталонное значение выхода нейронной сети для j – го примера.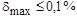 . При обучении нейронной сети размер популяции должен быть не менее 100 особей. В качестве кода при решении задачи будем использовать массив из 11 действительных чисел (табл. 8), по четыре на каждый скрытый нейрон и три для выходного нейрона, которые представляют собой веса соответствующих входов нейронов и параметры их функций активности. Для элементов хромосомы (особи) – генов – введем ограничения, обусловленные природой нейронных сетей:
. При обучении нейронной сети размер популяции должен быть не менее 100 особей. В качестве кода при решении задачи будем использовать массив из 11 действительных чисел (табл. 8), по четыре на каждый скрытый нейрон и три для выходного нейрона, которые представляют собой веса соответствующих входов нейронов и параметры их функций активности. Для элементов хромосомы (особи) – генов – введем ограничения, обусловленные природой нейронных сетей: 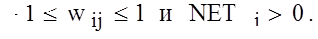 Для оператора скрещивания можно установить вероятность применения 0,95 и использовать элитизм. В качестве оператора мутации будем использовать случайное изменение значений весов и параметра функции активации для каждого нейрона на случайную величину. Вероятность мутации 0,01. Причем одновременно будет изменяться параметр функции только для одного нейрона, и для каждого нейрона будет изменяться один из входных весов. Какие конкретно веса и параметры будут меняться, определяется по равномерному закону. Например, мутация может быть следующей: значение
Для оператора скрещивания можно установить вероятность применения 0,95 и использовать элитизм. В качестве оператора мутации будем использовать случайное изменение значений весов и параметра функции активации для каждого нейрона на случайную величину. Вероятность мутации 0,01. Причем одновременно будет изменяться параметр функции только для одного нейрона, и для каждого нейрона будет изменяться один из входных весов. Какие конкретно веса и параметры будут меняться, определяется по равномерному закону. Например, мутация может быть следующей: значение 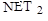 увеличивается на 0,1; значение
увеличивается на 0,1; значение 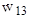 уменьшается на 0,01 и т.д. Исходная информация будет формироваться на основе равномерного распределения для каждого гена хромосомы (особи).
уменьшается на 0,01 и т.д. Исходная информация будет формироваться на основе равномерного распределения для каждого гена хромосомы (особи).