Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 9. Генетические алгоритмы.Содержание книги
Поиск на нашем сайте
В лекции рассмотрены методы поиска оптимальных решений многокритериальных прикладных задач управления системами в реальном времени с использованием эволюционных аналогий. Представлены основы теории генетических алгоритмов, построенных на принципах, сходных с принципами естественного отбора и генетики. Приведены примеры решения задач, в которых показаны эффективность генетических алгоритмов.
9.1. Эволюционные вычисления и традиционные методы оптимизации. Задача управления любым техническим комплексом или системой, включая электротехнические комплексы, является много критериальной, то есть такой, в которой приходится учитывать большое число факторов. Здесь аналитику приходится оценивать множество сил, влияний интересов и последствий, характеризующих то или иное решение. Зачастую решения требуется принимать в режиме, близком к реальному времени. Принятие правильного решения заключается в выборе такого варианта из числа возможных, в котором с учетом всех разнообразных факторов и противоречивых требований будет оптимизирована некая общая ценность, то есть решение будет в максимальной степени способствовать достижению поставленной цели. В качестве критерия оценки качества принимаемого решения выступает некая целевая функция, аргументами которой являются количественные характеристики, описывающие состояние факторов, влияющих на достижение цели в решаемой задаче. При этом решению, приводящему к наилучшему результату, как правило, соответствует экстремальное значение целевой функции, то есть точка ее максимума или минимума. В основе традиционных методов оптимизации лежат математические вычисления, позволяющие находить экстремум целевой функции. Ценность каждого такого метода заключается в том, что с помощью него можно найти точку экстремума целевой функции, не перебирая всех возможных комбинаций ее аргументов. Среди многочисленных подходов можно выделить три основных типа методов поиска оптимальных решений. · Методы, основанные на математических вычислениях подразделяются на направленные и ненаправленные. Суть ненаправленного метода состоит в том, что локальный экстремум ищется путем решения системы, как правило, нелинейных уравнений. Эта система составляется путем приравнивания градиента целевой функции к нулю (например, метод градиентного спуска или покоординатного спуска). Направленные методы строятся на перемещении от точки к точке в допустимой области, причем направление подобных перемещений связывается с направлением, на которое указывает градиент (например, метод касательных). К недостаткам этих методов можно отнести очень жесткие условия, накладываемые на целевую функцию. Она должна быть дифференцируема на всем пространстве поиска. При формализации современных задач это условие, как правило, выполнить не удается. Кроме того, данные методы находят лишь локальные экстремумы целевой функции, тогда как оптимальному решению соответствует только глобальный экстремум. Следовательно, методы поиска оптимальных решений, основанные на математических вычислениях, применимы лишь в случаях гладких, всюду дифференцируемых целевых функций, имеющих один экстремум на пространстве поиска. · Перечислительные методы основываются на том, что пространство поиска любой задачи можно представить в виде совокупности дискретных точек. Даже если пространство поиска непрерывно, то конечная точность представления чисел в компьютере позволяет сделать такое допущение. В этом случае поиск решения будет сводиться к перебору всех точек пространства поиска и вычислению в них целевой функции, в одной из которых она, несомненно, примет экстремальное значение. Недостаток этих методов очевиден. При увеличении числа аргументов целевой функции количество точек пространства значительно увеличивается, что приводит к значительным временным затратам и необходимости применения все более мощной и дорогостоящей вычислительной техники. В то же время размерность решаемых сейчас задач постоянно растет, а время, доступное для принятия решений сокращается. Следовательно, перечислительные методы также применимы для решения все более сужающегося класса задач. · Методы, использующие элементы случайного по иска в пространстве задачи с сохранением наилучшего полученного результата. Очевидно, что такие методы не гарантируют нахождение оптимальных решений, но могут к ним существенно приблизиться. Для этого в методы вносится свойство детерминированности, на чем основываются эволюционные вычисления. Эволюционные вычисления используется для описания алгоритмов поиска, основанных на некоторых формализованных принципах естественного эволюционного процесса. Основное преимущество эволюционных вычислений заключается в возможности решения задач с большой размерностью за счет сочетания элементов случайности и детерминированности точно так, как это происходит в природной среде. Детерминированность методов заключается в моделировании природных процессов отбора, размножения и наследования, происходящих по строго определенным правилам. Основным правилом при этом является закон эволюции: «выживает сильнейший», который обеспечивает улучшение находимого решения. Другим важным фактором эффективности эволюционных вычислений является моделирование размножения и наследования. Рассматриваемые варианты решений могут по определенному правилу порождать новые решения, которые будут наследовать лучшие черты своих «предков». В качестве случайного элемента в методах эволюционных вычислений может использоваться, например, моделирование процесса мутации. В этом случае характеристики того или иного решения могут быть случайно изменены, что приведет к новому направлению в процессе эволюции решений и может ускорить процесс выработки лучшего решения. История эволюционных вычислений началась с разработки ряда независимых моделей эволюционного процесса. Среди этих моделей можно выделить три основные парадигмы – это: 1. генетические алгоритмы, 2. эволюционные стратегии, 3. эволюционное программирование. Отличительной особенностью генетических алгоритмов является представление любой альтернативы решения в виде битовой строки фиксированной длины, манипуляции с которой производятся в отсутствие всякой связи с ее смысловой интерпретацией, то есть применяется единое универсальное представление любой задачи. Эволюционные стратегии представляют каждую из альтернатив решения единым массивом численных параметров. По существу за каждым массивом скрывается аргумент целевой функции. Воздействие на данные массивы осуществ ляется с учетом их смыслового содержания и направлено на улучшение значений входящих в них параметров. Эволюционное программирование основано на представлении альтернатив решений в виде моделей-автоматов, описывающих средствами формальной логики возможные переходы исследуемой системы из некоторого начального состояния в заключительное состояние. Эволюционная программа при этом реализует моделирование процессов естественной эволюции моделей-автоматов, когда в каждый момент времени сохраняется тот «организм», который может наилучшим способом справится с данной задачей. Эволюционные вычисления не гарантируют обнаружения глобального экстремума целевой функции, однако они демонстрируют эффективность решений ряда практических задач по проектированию, планированию, управлению, прогнозированию во многих областях техники. Отрицательной чертой э волюционных вычислений является то, что они представляют собой скорее подход к решению задач оптимизации, чем алгоритм. Вследствие этого они требуют адаптации к каждому конкретному классу задач путем выбора определенных характеристик и параметров. Генетические алгоритмы. Генетический алгоритмпредставляет собойпоисковый алгоритм, основанный на природных механизмах селекции и генетики. Он работает с кодами безотносительно их смысловой интерпретации. Поэтому сам код и его структура описываются понятием генотип, а его интерпретация, с точки зрения решаемой задачи, понятием фенотип. Каждый код представляет, по сути, точку пространства поиска. С целью максимально приблизиться к биологическим терминам, экземпляр кода называют хромосомой или особью. В обозначении строки кода будем использовать термин «особь». На каждом шаге работы генетический алгоритм использует несколько точек поиска одновременно. Совокупность этих точек в пространстве поиска является набором особей или популяцией. Количество особей в популяции называют размером популяции. Размер популяции является фиксированным и представляет одну из характеристик генетического алгоритма. Формирование исходной популяции происходит с использованием какого-либо случайного закона, на основе которого выбирается нужное количество точек поискового пространства. На каждом шаге работы генетический алгоритм обновляет популяцию путем создания новых особей и уничтожения старых. Чтобы отличать популяции на каждом из шагов и сами эти шаги, их называют поколениями и обычно идентифицируют по номеру. Например, популяция, полученная из исходной популяции после первого шага работы алгоритма, будет первым поколением, после следующего шага - вторым, и т.д. В процессе работы алгоритма генерация новых особей происходит на основе моделирования процесса размножения. При этом, естественно, порождающие особи называются родителями, а порожденные соответственно - потомками. Родительская пара, как правило, порождает пару потомков. Непосредственная генерация новых кодовых строк из двух выбранных происходит за счет работы оператора скрещивания, который также называют кроссинговером. При порождении новой популяции оператор скрещивания может применяться не ко всем парам родителей. Часть этих пар может переходить в популяцию следующего поколения непосредственно. Насколько часто будет возникать такая ситуация, зависит от значения вероятности применения оператора скрещивания, которая является одним из параметров генетического алгоритма. Вероятность применения оператора скрещивания обычно выбирается в пределах от 0,9 до 1, чтобы обеспечить появление новых особей, расширяющих пространство поиска. При значении вероятности меньше единицы часто используют особую стратегию - элитизм, которая предполагает переход в популяцию следующего поколения элиты, то есть лучших особей текущей популяции, без всяких изменений. Применение элитизма способствует сохранению общего качества популяции на высоком уровне. При этом элитные особи участвуют еще и в процессе отбора родителей для последующего скрещивания. Количество элитных особей определяется по формуле, Моделирование процесса мутации новых особей осуществляется за счет работы оператора мутации. Основным параметром оператора мутации также является вероятность мутации. Поскольку размер популяции фиксирован, то порождение потомков должно сопровождаться уничтожением других особей. Выбор пар родителей из популяции для порождения потомков производит оператор отбора, а выбор особей для уничтожения - оператор редукции. Основным параметром их работы является, как правило, качество особи, которое определяется значением целевой функции в точке пространства поиска, описываемой этой особью. В основе оператора отбора лежит принцип «выживает сильнейший». Выбор особи для размножения производится случайно. Вероятность участия особи в процессе размножения определяется по формуле Таким образом, можно перечислить основные понятия и термины, используемые в области генетических алгоритмов: генотип и фенотип; особь и качество особи; К характеристикам генетического алгоритма относятся: размер популяции; оператор скрещивания и вероятность его использования; оператор мутации и вероятность мутации; оператор отбора; оператор редукции; критерий останова. Операторы отбора, скрещивания, мутации и редукции называют еще генетическими операторами. Критерием останова работы генетического алгоритма может быть одно из трех событий: · формирование заданного пользователем числа поколений; · достижение популяции заданного пользователем качества; · достижение уровня сходимости, при котором дальнейшее улучшение особей в популяции происходит чрезвычайно медленно. Характеристики генетического алгоритма определяются путем подбора, обеспечивающего поиск лучшего решения задачи за малое время работы. Рассмотрим примеры применения генетических алгоритмов при решении оптимизационных задач.
Пример поиска максимума одномерной функции. Пусть имеется набор натуральных чисел от 0 до 31 и функция При решении задачи используем в качестве кода двоичное представление аргументов функции. Это положение представляет собой фенотип решаемой задачи. Сам код будет представлять собой двоичную строку из пяти бит. Это генотип алгоритма. Функция 1. Размер начальной популяции N можно выполнять произвольным образом, например подбрасыванием монеты; 2. Вероятность оператора скрещивания 3. Вероятность оператора мутации Пусть процесс мутации заключается в инверсии одного из битов строки, выбираемого случайно по равномерному закону; вероятность оператора мутации равна 0,001; размер популяции Таблица 5 Исходная популяция из четырех особей.
Предположим, что оператор отбора выбрал для производства потомков две пары строк (1,2) и (2,4). В каждой паре разбиение на подстроки оператором скрещивания происходит независимо (табл. 6). Таблица 6 Работа оператора скрещивания
Пусть оператор мутации, несмотря на низкую вероятность 0,001, изменяет значение кода потомка в третьей строке (табл.6) с 10000 на 10001. Тогда за счет порожденных потомков популяция расширяется до восьми особей. Оператор редукции сокращает популяцию до исходного числа особей, исключая те особи, в которых значения целевой функции минимальны (табл. 7). Таблица 7. Популяция первого поколения особей.
На этом шаг работы генетического алгоритма заканчивается. Очевидно, что даже за эту одну итерацию качество популяции значительно возросло. Лучшее решение увеличилось с 18 до 27 при оптимальном решении 31.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.008 с.) |

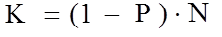 где К – количество элитных особей, Р - вероятность применения оператора скрещивания, N – размер популяции. В случае использования элитизма все выбранные родительские пары подвергаются скрещиванию, несмотря на то, что вероятность применения оператора скрещивания меньше единицы, что позволяет сохранить прежний размер популяции.
где К – количество элитных особей, Р - вероятность применения оператора скрещивания, N – размер популяции. В случае использования элитизма все выбранные родительские пары подвергаются скрещиванию, несмотря на то, что вероятность применения оператора скрещивания меньше единицы, что позволяет сохранить прежний размер популяции.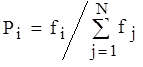 , где i – номер особи,
, где i – номер особи, 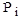 - вероятность участия особи в процессе размножения,
- вероятность участия особи в процессе размножения, 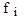 - значение целевой функции для i -ой особи. Очевидно, что одна особь может быть задействована в нескольких родительских парах.
- значение целевой функции для i -ой особи. Очевидно, что одна особь может быть задействована в нескольких родительских парах.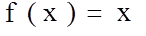 , определенная на этом наборе чисел. Требуется найти максимальное значение функции.
, определенная на этом наборе чисел. Требуется найти максимальное значение функции.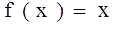 является целевой функцией. При задании характеристик генетического алгоритма будем исходить из следующих правил:
является целевой функцией. При задании характеристик генетического алгоритма будем исходить из следующих правил: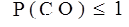 ;
;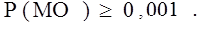
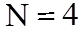 (табл. 5); в связи с простейшей задачей стратегия элитизма в алгоритме не применяется.
(табл. 5); в связи с простейшей задачей стратегия элитизма в алгоритме не применяется.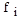
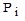
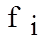 для потомков
для потомков
 1011
1011