
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель искусственного нейрона.Содержание книги
Поиск на нашем сайте
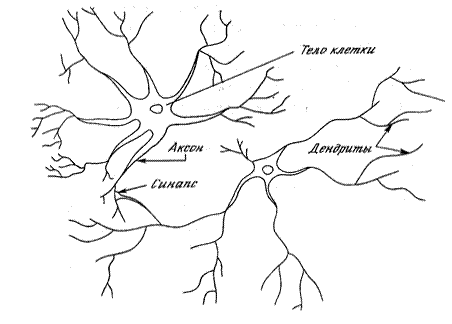
Искусственная нейронная сеть (ИНС) - это упрощенная модель биологического мозга, точнее нервной ткани. Нервная система человека, построенная из элементов, называемых нейронами, имеет поразительную сложность. Около 1011 нейронов участвуют в примерно 1015 передающих связях, имеющих длину метр и более. Каждый нейрон обладает многими качествами, общими с другими элементами тела, но его уникальной способностью является прием, обработка и передача электрохимических сигналов по нервным путям, которые образуют коммуникационную систему мозга. Структура пары типичных биологических нейронов показана на рис. 39. Нейрон состоит из тела (сомы),содержащего ядро, и отростков - дендритов, по которым в нейрон поступают входные сигналы. Один из отростков, ветвящийся на конце, служит для передачи выходных сигналов данного нейрона другим нервным клеткам. Он называется аксоном.Соединение аксона с дендритом другого нейрона называется синапсом.Нейрон возбуждается и передает сигнал через аксон, если число пришедших по дендритам возбуждающих сигналов больше, чем число тормозящих. Несмотря на то, что у этой функциональной схемы нейрона много усложнений и исключений, большинство искусственных нейронных сетей моделируют лишь эти простые свойства.
Рис. 39. Биологический нейрон.
Искусственный нейрон (рис. 40), далее просто нейрон, задается совокупностью своих входов, обозначенных
Сигнал NET преобразуется функцией активации F и дает выходной сигнал нейрона
Рис.41. Искусственный нейрон с активационной функцией F. На рис.41 блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется сигмоидальная (S-образная) функция, показанная на рис.42.
Рис. 42. Сигмоидальная функция. Эта функция имеет вид:
Рис. 43. Функция гиперболического тангенса. Простейшими формами функции активации являются линейная и ступенчатая (пороговая) функции. Линейная функция активации дифференцируема и легко вычисляется, что в ряде случаев позволяет уменьшить ошибки выходных сигналов в ИНС. Однако она не универсальна и не обеспечивает решение многих плохо формализованных задач. Ступенчатая функция обычно задается в виде единичной функции с жесткими ограничениями: она равна нулю, если NET < 0, и единице, если NET
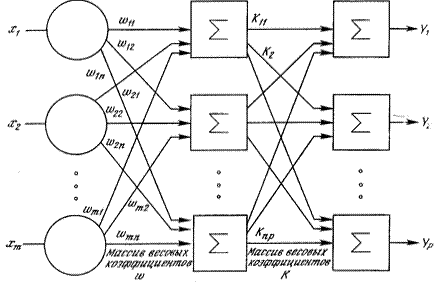
Модели нейронных сетей. Нейронная сеть представляет собой совокупность искусственных нейронов, организованных слоями. Реальная нейронная сеть может содержать один или большее количество слоев и соответственно характеризоваться как однослойная или как многослойная, с обратными связями и без них. Многослойные сети отличаются от однослойных тем, что между входными и выходными данными располагаются несколько так называемых скрытых слоев нейронов, добавляющих больше нелинейных связей в модель. Простейшая сеть состоит из группы нейронов, образующих один слой (рис. 44). На рисунке вершины - круги слева служат лишь для распределения входных сигналов. Они не выполняют каких - либо вычислений, и поэтому не будут считаться слоем. По этой причине они обозначены кругами, чтобы отличать их от вычисляющих нейронов, обозначенных квадратами. Каждый элемент из множества входов Х отдельным весом соединен с каждым искусственным нейроном, и каждый нейрон выдает взвешенную сумму входов в сеть. В искусственных и биологических сетях многие соединения могут отсутствовать, поэтому на рисунке все соединения показаны в целях общности. Многослойные сети обладают большими вычислительными возможностями, чем однослойные. Послойная организация нейронов копирует слоистые структуры определенных отделов мозга. Многослойные сети могут образовываться каскадами слоев: выход одного слоя является входом для последующего слоя. Двухслойная сеть со всеми соединениями показана на рис. 45. Если функция активации является линейной, то нейронная сеть также будет линейной. Двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц, то есть
Рис. 44. Однослойная нейронная сеть
Рис. 45. Двухслойная нейронная сеть. По архитектуре связей нейронные сети могут быть сгруппированы в два класса: сети прямого распространения, в которых обратные связи отсутствуют (нет соединений, идущих от выходов некоторого слоя к входам этого же слоя или предшествующих слоев) и сети рекуррентного типа, в которых возможны обратные связи. В сетях прямого распространения нет памяти, их выход полностью определяется текущими входами и значениями весов. Сети прямого распространения подразделяются на однослойные перцепротроны (сети) и многослойные перцептроны (сети). Название перцептрон для нейросетей введено Ф. Розенблаттом, разработчиком первой нейросети (1957 г.). Он же доказал сходимость области решений для перцептрона при его обучении. Реккурентные сети могут обладать свойствами, сходными с кратковременной человеческой памятью. Класс рекуррентных нейронных сетей гораздо обширнее и сложнее по своему устройству. Поведение рекуррентных сетей описывается дифференциальными или разностными уравнениями, как правило, первого порядка. Это гораздо расширяет области применения нейросетей и способы их обучения. Сеть организована так, что каждый нейрон получает входную информацию от других нейронов, возможно, и от самого себя, и от окружающей среды. Этот тип сетей имеет важное значение для моделирования нелинейных динамических систем. Среди рекуррентных сетей можно выделить сети Хопфилда и сети Кохонена. При всем многообразии возможных конфигураций ИНС на практике получили распространение лишь некоторые из них. Классическим моделями нейронных сетей являются: 1. Многослойные перцептроны содержат помимо входного и выходного слоев так называемые скрытые слои. Они представляют собой нейроны, которые не имеют непосредственных входов исходных данных, а связаны только с выходами входного слоя и с входом выходного слоя. Таким образом, скрытые слои дополнительно преобразуют информацию и добавляют нелинейности в модели. Многослойный перцептрон с сигмоидальными функциями активации способен аппроксимировать любую функциональную зависимость (доказано в виде теоремы), однако при этом не известно ни нужное число слоев, ни нужное количество скрытых нейронов, ни необходимое для обучения сети время. Эти проблемы до сих пор не решены; 2. Сети Хопфилда строятся из N нейронов, связанных каждый с каждым кроме самого себя, причем все нейроны являются выходными. Нейронную сеть можно использовать в качестве ассоциативной памяти, а также для обработки неупорядоченные, упорядоченных во времени или пространстве образцов (рукописные буквы, временные ряды, графики); 3. Сети Кохонена еще называют «самоорганизующимися картами признаков». Сеть рассчитана на самостоятельное обучение. В процессе обучения на вход сети подаются различные образцы. Сеть улавливает особенности их структуры и разделяет образцы на кластеры, а затем уже обученная сеть относит каждый вновь поступающий пример к одному из кластеров, руководствуясь некоторым критерием «близости». Сеть состоит из одного входного и одного выходного слоя. Количество элементов в выходном слое непосредственно определяет, сколько различных кластеров сеть сможет распознать. Каждый из выходных элементов получает на вход весь входной вектор. Как и во всякой нейронной сети, каждой связи приписан некоторый синаптический вес. В большинстве случаев каждый выходной элемент соединен также со своими соседями. Эти внутрислойные связи играют важную роль в процессе обучения, так как корректировка весов происходит только в окрестности того элемента, который наилучшим образом откликается на очередной вход. Выходные элементы соревнуются между собой за право вступить в действие «получить урок». Выигрывает тот из них, чей вектор весов окажется ближе всех к входному вектору. Структура ИНС, включая определение числа слоев и числа нейронов в каждом слое, формируется до начала обучения, поэтому успешное решение этой проблемы во многом зависит от опыта и искусства аналитика, проводящего исследование.
Обучение нейронных сетей. Главное отличие и преимущество нейросетей перед классическими средствами прогнозирования и классификации заключается в их способности к обучению. На этапе обучения происходит вычисление синаптических коэффициентов в процессе решения нейронной сетью задач, в которых нужный ответ определяется не по правилам, а с помощью примеров, сгруппированных в обучающие множества. Нейросеть на этапе обучения сама выполняет роль эксперта в процессе подготовки данных для построения экспертной системы. Предполагается, что правиланаходятся в структуре обучающих данных. Такие данные представляют собой ряды примеров с указанием для каждого из них значения выходного параметра, которое было бы желательно получить. Действия, которые при этом происходят, можно назвать обучение с учителем. На вход сети подается вектор исходных данных, а на выходной узел сообщается желаемое значение результата вычислений. Контролируемое обучение нейросети можно рассматривать как решение оптимизационной задачи. Ее целью является минимизация функции ошибок на данном множестве примеров путем выбора значений весов W. Достижение минимума называется сходимостью процесса обучения. Поскольку ошибка зависит от весов нелинейно, получить решение в аналитической форме невозможно, и поиск глобального минимума осуществляется посредством итерационного процесса, так называемого обучающего алгоритма. В настоящее время используются более сотни разных обучающих алгоритмов, отличающихся друг от друга стратегией оптимизации и критерием ошибок. Обычно в качестве меры погрешности берется средняя квадратичная ошибка
где M – число примеров в обучаемом множестве. Среди обучающих алгоритмов наиболее распространенным является алгоритм обратного распространения ошибок. Согласно методу перед началом обучения сети всем межнейронным связям присваиваются небольшие случайные значения весов. Каждый шаг обучающей процедуры состоит из двух фаз. Во время первой фазы входные элементы сети устанавливаются в заданное состояние. Входные сигналы распространяются по сети, порождая некоторый выходной вектор. При этом используются сигмоидальные функции активации. Полученный выходной вектор сравнивается с требуемым (правильным) вектором. Если они совпадают, то весовые коэффициенты связей не изменяются. В противном случае вычисляется разница между фактическими и требуемыми выходными значениями, которая передается последовательно от выходного слоя к входному слою. На основе этой информации проводится модификация весов связей в соответствии с формулой:
где Общая ошибка функционирования сети определяется по формуле:
где Когда величина ошибки достигает приемлемо малого уровня, обучение останавливают, и сеть готова к выполнению возложенных на нее задач. Важно отметить, что вся информация, которую сеть приобретает о задаче, содержится в наборе примеров. Поэтому качество обучения сети зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают задачу. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров. Если не для всех примеров обучающей выборки известны правильные ответы, то обучение сети проводится без учителя. В этом случае применение самонастраивающихся сетей Кохонена дает возможность определить внутреннюю структуру поступающих в сеть данных и распределить образцы по категориям. Несмотря на многочисленные успешные применения алгоритма обратного распространения при обучении ИНС, у него есть недостатки. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Длительное время обучения может быть результатом неоптимального выбора шага сети Неудачи в обучении сети обычно возникают по двум причинам. 1. Паралич сети. В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага, но это увеличивает время обучения. Для предохранения от паралича применяются различные эвристики, но пока что они могут рассматриваться лишь как экспериментальные. 2. Попадание в локальный минимум. Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении минимума. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть не может из него выбраться.
Способы реализации ИНС. Нейронные сети могут быть реализованы программным или аппаратным способами. Вариантом аппаратной реализации являются нейрокомпьютеры. Большинство современных нейрокомпьютеров представляют собой персональный компьютер, снабженный дополнительной нейроплатой. Повышенный интерес вызывают специализированные нейрокомпьютеры, в которых реализованы принципы архитектуры нейронных сетей. В тех случаях, когда разработка или внедрение аппаратных реализаций нейронных сетей обходится слишком дорого, применяют более дешевые программные реализации. Программу моделирования нейронной сети обычно называют программой-имитатором или нейропакетом, понимая под этим программную оболочку, эмулирующую для пользователя среду нейрокомпьютера на обычном компьютере. В настоящее время на рынке программного обеспечения имеется множество самых разнообразных программ для моделирования нейронных сетей. В них воплощены практически все известные алгоритмы обучения и топологии нейросетей. Общее число фирм, разрабатывающих эти средства, превышает 150. Несмотря на сложность заложенных в нейропакетах методов, использовать их довольно просто. Они позволяют сконструировать, обучить, протестировать и использовать в работе нейронную сеть на основе понимания нескольких базовых теоретических положений, изложенных выше. Первые подобные программные продукты появились на Западе в середине 80 -х годов XX века. Одним из лидеров этого рынка стал нейросетевой пакет BrainMaker американской фирмы California Scientific Software. В настоящее время нейрокомпьютерный сегмент рынка программного обеспечения бурно развивается, и появление новых пакетов – естественный процесс. Современные продукты во многом лучше своих предшественников – улучшен интерфейс пользователя, появились дополнительные нейропарадигмы, в пакетах реализованы возможности взаимодействия с другими приложениями посредством механизмов OLE, ActiveX и др. Плата за эти возможности использовать более мощный, чем ранее компьютер, рост требований к объему оперативной и дисковой памяти. Кроме того, новый пакет не гарантирует более качественного решения прикладной задачи пользователя. В большей степени это качество зависит от правильно поставленной задачи, выбора данных. Эффективным реальным инструментом для расчета и проектирования нейронных сетей при решении многочисленных прикладных задач во многих областях техники, в том числе электротехники и электроники, электрооборудования является пакет прикладных программ Neural Network Toolbox (ППП NNT), функционирующий под управлением системы Matlab версии 5.3 и 6.0. Следует также обратить внимание на интерфейс ППП NNT с системой Simulink, что позволяет наглядно отобразить архитектуру сети и выполнить моделирование как статических, так и динамических нейронных сетей. Последнее обстоятельство особенно важно при построении систем управления различными электротехническими объектами, диагностики их состояния и поведения.
|
||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.239 (0.009 с.) |

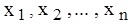 , весами входов
, весами входов 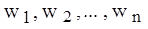 , функцией состояния NET и функцией активации F. Функция состояния определяет состояние нейрона в зависимости от значений его входов, весов входов и, возможно, предыдущих состояний. Наиболее часто используются функции состояния, вычисляемые как сумма произведений значений входов на веса соответствующих входов по всем входам
, функцией состояния NET и функцией активации F. Функция состояния определяет состояние нейрона в зависимости от значений его входов, весов входов и, возможно, предыдущих состояний. Наиболее часто используются функции состояния, вычисляемые как сумма произведений значений входов на веса соответствующих входов по всем входам 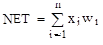 . Суммирующий блок, соответствующий телу биологического нейрона, складывает взвешенные входы алгебраически, создавая выход, который будем называть NET.
. Суммирующий блок, соответствующий телу биологического нейрона, складывает взвешенные входы алгебраически, создавая выход, который будем называть NET.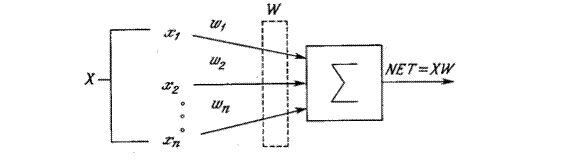

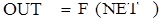 .
.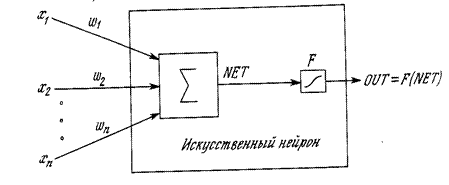
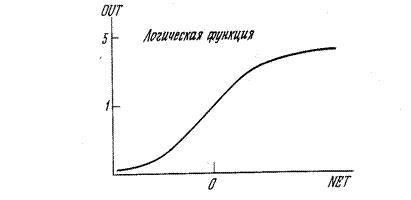
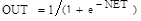 . По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Центральная область сигмоидальной функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время как области с падающим усилением на положительном и отрицательном концах подходят для больших возбуждений. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала. Другой широко используемой функцией активации является гиперболический тангенс OUT = th(x). Подобно сигмоидальной функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET = 0 значение выходного сигнала OUT равно нулю (рис. 43). В отличие от сигмоидальной функции гиперболический тангенс принимает значения различных знаков, что оказывается выгодным при поиске экстремума в пространстве параметров ИНС.
. По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Центральная область сигмоидальной функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время как области с падающим усилением на положительном и отрицательном концах подходят для больших возбуждений. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала. Другой широко используемой функцией активации является гиперболический тангенс OUT = th(x). Подобно сигмоидальной функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET = 0 значение выходного сигнала OUT равно нулю (рис. 43). В отличие от сигмоидальной функции гиперболический тангенс принимает значения различных знаков, что оказывается выгодным при поиске экстремума в пространстве параметров ИНС.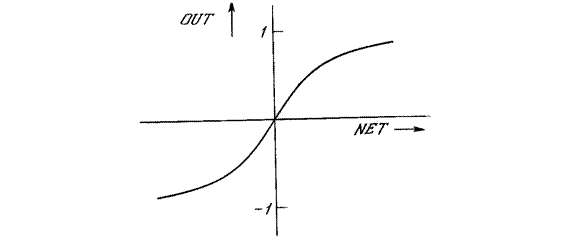
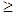 0. Такая функция не обеспечивает достаточной гибкости ИНС при обучении. Рассмотренная простая модель искусственного нейрона игнорирует многие свойства своего биологического двойника. Например, она не принимает во внимание задержки во времени, которые воздействуют на динамику системы. Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему.
0. Такая функция не обеспечивает достаточной гибкости ИНС при обучении. Рассмотренная простая модель искусственного нейрона игнорирует многие свойства своего биологического двойника. Например, она не принимает во внимание задержки во времени, которые воздействуют на динамику системы. Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему.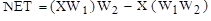 . Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной однослойной сетью. Для расширения вычислительных возможностей ИНС применяется нелинейная функция активации.
. Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной однослойной сетью. Для расширения вычислительных возможностей ИНС применяется нелинейная функция активации.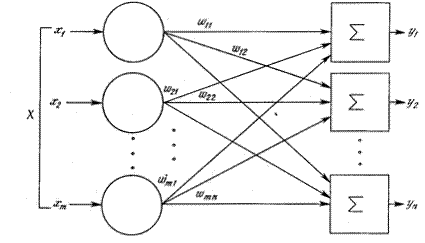
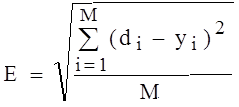 ,
,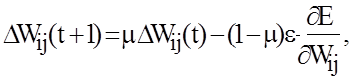
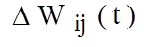 - изменение веса связи на шаге итерации t обучающей пары вход-выход i -го нейрона, получающего входной сигнал, и j –го нейрона, посылающего выходной сигнал; m - коэффициент, задаваемый пользователем в интервале (0,1); e - величина шага сети или мера точности обучения сети. В современных нейросетевых пакетах пользователь может сам определять, как будет изменяться величина шага сети, очень часто по умолчанию берется линейная или экспоненциальная зависимость величины шага от количества итераций сети. Чем меньше шаг сети, тем больше времени потребуется на обучение сети и тем возможнее станет ее попадание в окрестность локального минимума ошибки.
- изменение веса связи на шаге итерации t обучающей пары вход-выход i -го нейрона, получающего входной сигнал, и j –го нейрона, посылающего выходной сигнал; m - коэффициент, задаваемый пользователем в интервале (0,1); e - величина шага сети или мера точности обучения сети. В современных нейросетевых пакетах пользователь может сам определять, как будет изменяться величина шага сети, очень часто по умолчанию берется линейная или экспоненциальная зависимость величины шага от количества итераций сети. Чем меньше шаг сети, тем больше времени потребуется на обучение сети и тем возможнее станет ее попадание в окрестность локального минимума ошибки.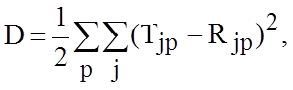
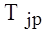 и
и 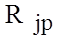 - соответственно желательное и действительное значение выходного сигнала j – го блока для p – й обучающей пары нейронов вход-выход.
- соответственно желательное и действительное значение выходного сигнала j – го блока для p – й обучающей пары нейронов вход-выход.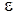 .
.


