
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скоростей и ускорений структурных групп
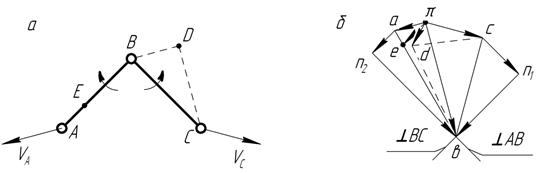
3.5.1. Группа Ассура 1-го вида (рис. 3.7, а) Дано: скорости точек Выразим скорость точки В в виде суммы векторов переносного и относительного движения
Рис. 3.7. Построение плана скоростей структурной группы 1-го вида. Скорость точки В неизвестна ни по величине, ни по направлению. Относительные скорости Система векторных уравнений определима, если число уравнений равно числу неизвестных, умноженному на 2. Наша система содержит два векторных уравнения и четыре неизвестных, то есть является определимой. Строим план скоростей (рис. 3.7, б). Откладываем произвольный отрезок ра в направлении вектора
С учетом масштабного коэффициента откладываем отрезок рс в направлении вектора
Через точку а проводим прямую, перпендикулярную АВ, через точку с —прямую, перпендикулярную ВС. Точка пересечения этих прямых (направлений относительных скоростей) определяет общее решение двух уравнений (3.31). Скорость точки D определяем по принципу подобия. Для этого строим на отрезке bс подобный и сходственный треугольник (
Скорость точки Е определяем также по принципу подобия
отсюда
Отложив на отрезке аb плана скоростей длину отрезка ае, соединяем точку е с полюсом и определяем скорость точки Е:
Далее определяем угловые скорости звеньев
где
АВ, ВС — отрезки на плане механизма, изображающие длины звеньев в масштабе;
Для того, чтобы определить направления угловых скоростей, векторы относительных скоростей Аналогичным образом строится план ускорений. Разница заключается лишь в том, что относительные ускорения раскладываются на две составляющие: нормальную и касательную.
Дано: ускорения точек Определить: ускорения точек Векторные уравнения для построения плана ускорений
Векторы Касательные составляющие относительных ускорений известны только по направлению: Таким образом, имеется два векторных уравнения с четырьмя неизвестными, решая которые, определяем абсолютное ускорение
Рис. 3.8. Построение плана ускорений структурной группы 1-го вида
Из полюса отрезок произвольной длины Определяем масштабный коэффициент плана ускорений
С учетом масштаба строим все остальные векторы. Ускорение точки С — в виде отрезка
Из точек а и с откладываем в масштабе векторы
Через точки n и n 1 проводим прямые, соответствующие направлениям касательных ускорений (через точку n — перпендикуляр к звену АВ, через точку n 1 — перпендикуляр к звену ВС). Точка пересечения этих двух прямых определяет ускорение точки В
Ускорения точек D и Е определяются по правилу подобия; для этого на отрезке bc, изображающем полное относительное ускорение
Из пропорционального деления отрезков определяют отрезок, изображающий ускорение точки Е:
а затем длину отрезка πе умножают на масштабный коэффициент
Величину и направления угловых ускорений находят по касательным составляющим относительных ускорений (см. рис. 3.8, б)
Направления угловых ускорений звеньев определяют, мысленно перенося векторы
Группа Ассура 2-го вида Построение планов скоростей и ускорений рассмотрим на примере кривошипно-ползунного механизма (рис. 3.9). Порядок построения, обозначения, формулы аналогичны рассмотренным выше, поэтому этот и последующий разделы даны в сокращенной форме, без повторения ранее изложенных правил. Дано: кинематическая схема механизма; угловая скорость кривошипа Определить: скорость и ускорение точки В; угловую скорость и угловое ускорение звена АВ. Механизм образован присоединением к ведущему звену группы Ассура II класса 2-го вида. Выделим эту группу и построим для нее план скоростей (рис. 3.9, б). Скорость точки В определится уравнением:
Известны величина и направление скорости точки А
Известны также направления скоростей : Отрезок ра, изображающий скорость точки А на плане, выбираем произвольным по величине. Масштабный коэффициент Через точку А проводим направление относительной скорости
Рис. 3.9. Пример построения плана скоростей и ускорений структурной группы 2-го вида: а — план механизма; б — план скоростей; в — план ускорений Определяем скорость точки В, измерив отрезок р b на плане и умножив его на масштабный коэффициент
Угловая скорость звена АВ
Вектор относительной скорости показывает, что звено АВ вращается против часовой стрелки (см. рис. 3.9). План ускорений строим по уравнению:
где Вектор касательного ускорения Векторабсолютного ускорения aB направлен параллельно x - x. Точка пересечения направлений двух последних векторов определяет абсолютное ускорение, а также направление и величину касательного ускорения. На плане ускорений, построенном с учетом масштабного коэффициента
Угловое ускорение звена АВ находим по касательной составляющей
Направление углового ускорения находим, перенося вектор касательной составляющей ускорения
Группа Ассура 3-го вида Построение планов скоростей и ускорений рассмотрим на примере кулисного механизма, который образован присоединением к механизму I класса группы Ассура II класса 3-го вида (рис. 3.10). Дано: кинематическая схема механизма; угловая скорость кривошипа Определить: скорость и ускорение точек В' и D кулисы; угловую скорость и угловое ускорение кулисы. Строим план скоростей (рис. 3.10, б) по векторному уравнению
где
Имеем одно векторное уравнение с двумя неизвестными: величиной VВ' и величиной VВ'В. Перпендикулярно радиусу вращения (длине кривошипа) АВ откладываем отрезок произвольной величины, изображающий известную скорость
Через точку b проводим направление относительной скорости (параллельно кулисе DC); через полюс — направление абсолютной скорости точки В' (перпендикулярно кулисе). Точка пересечения определяет скорость точки В' кулисы
Рис. 3.10. Пример построения плана скоростей и ускорений структурной группы 3-го вида: а — план механизма; б — план скоростей; в — план ускорений.
Скорость точки D находим по принципу подобия: строим на плане скоростей отрезок pd, пропорциональный длине кулисы CD
Абсолютная скорость точки D определяется отрезком pd с учетом масштабного коэффициента Угловая скорость кулисы
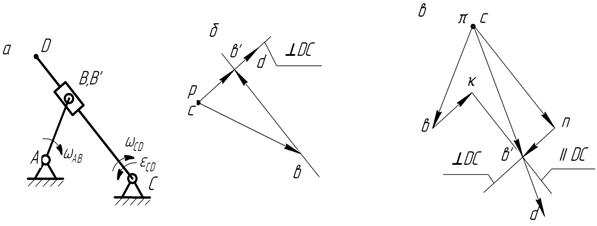
Направление угловой скорости находим, мысленно перенося вектор относительной скорости с плана скоростей в соответствующую точку механизма. Кулиса вращается по часовой стрелке (см. рис. 3.10, а, б). План ускорений строим по векторному уравнению
где
Второй член уравнения — Кориолисово ускорение, вычисляем его по формуле:
где Направление Кориолисова ускорения определяем поворотом вектора относительной скорости (bb' — на плане скоростей) на 90° в направлении угловой скорости кулисы
Через точку k проводим параллельно С D направление релятивного ускорения. Величина этого ускорения неизвестна, поэтому требуется составить еще одно векторное уравнение. Кулиса вращается неравномерно, поэтому ускорение точки В во вращательном движении вокруг точки С складывается из нормального и касательного
где
Откладываем в направлении от В' к С отрезок, изображающий нормальную составляющую ускорения (см. рис. 3.10, в):
Через точку n проводим направление касательного ускорения (перпендикулярно кулисе). Получаем точку пересечения b', которая определяет ускорение точки В' кулисы
Ускорение точки D находим по принципу подобия
Угловое ускорение кулисы определяем по касательной составляющей
Направление углового ускорения находим, перенося вектор
3.6. Аналоги скоростей и ускорений Во многих случаях при проектировании машин и механизмов законы движения звеньев в функции времени можно определить только на последующих стадиях проектирования, обычно после динамического анализа с учетом приложенных сил [2, с. 61]. В таких случаях движение звеньев определяется в два этапа: сначала устанавливаются зависимости кинематических параметров в функции обобщенной координаты (угла поворота ведущего звена), а затем определяется закон изменения обобщенной координаты во времени. Для выполнения подобных расчетов вводятся понятия аналогов скоростей и ускорений. Аналогом скорости какой-либо точки называется первая производная радиус-вектора этой точки по обобщенной координате. Для поступательного движения перемещение точки можно считать равным радиус-вектору. Тогда аналог скорости согласно определению
где
Скорость данной точки
Учитывая формулу (3.37), получаем связь между истинной скоростью и ее аналогом:
где Физический смысл аналога скорости - это скорость той же точки при Аналогом ускорения точки называется вторая производная радиус-вектора точки по обобщенной координате. Чтобы установить связь ускорения с аналогом ускорения продифференцируем (3.39) по времени
Окончательно получим
где
При вращательном движении звена вводятся понятия аналогов угловых скоростей и ускорений. Аналогом угловой скорости называется первая производная от угла поворота по обобщенной координате механизма
Где Угловая скорость звена
Аналогом углового ускорения называется вторая производная от угла поворота звена по обобщенной координате механизма. Дифференцируя (3.43) по времени, получим
Из формул (3.43) и (3.44) видно, что аналоги угловых скоростей и угловых ускорений являются безразмерными величинами.
3.7. Графическое дифференцирование и интегрирование как Графическое изображение изменения основных кинематических параметров механизма за полный цикл движения называется кинематической диаграммой. Если одна из кинематических функций задана в форме графика или в виде таблицы значений, то найти производную или интеграл от этой функции непосредственно в аналитической форме невозможно. В этом случае используют методы графического дифференцирования и интегрирования. Основное достоинство данного метода, как и у большинства графических методов, - это наглядность и простота; недостаток - невысокая точность по сравнению с аналитическими методами. Метод основан на геометрическом смысле производной, которая представляет собой тангенс угла наклона касательной в данной точке кривой к оси абсцисс. Обычно кривую заменяют ломаной линией и принимают следующее допущение: угол наклона касательных в точках, расположенных посередине каждого участка кривой, равен углу наклона соответствующей хорды. Это вносит некоторую погрешность, но она не суммируется, что обеспечивает приемлемую точность метода [2, с. 110]. На рис. 3.11 изображена кинематическая диаграмма перемещений точки в масштабе. Пусть за бесконечно малый промежуток времени Δt перемещение точки увеличилось на ΔS. Тогда скорость точки на этом участке определится из выражения
Рис. 3.11. К определению кинематических параметров методом кинематических диаграмм.
Из чертежа (см. рис. 3.11) следует, что ΔS/Δt =tgα, а с учетом принятого допущения это и есть первая производная (в пределе хорда превратится в касательную). Поэтому
Проведем из точки Р, расположенной влево от оси абсцисс на произвольном расстоянии Н, прямую, параллельную хорде ab, до пересечения с осью ординат. Эта прямая отсекает на оси ординат отрезок ОА, длина которого определяется из треугольника АОР
Разделив (3.46) на (3.47), получим
Правая часть уравнения содержит только постоянные величины, следовательно, она является также величиной постоянной и представляет собой масштабный коэффициент скорости.
Таким образом, отрезок ОА, отсекаемый лучом РА на оси ординат, изображает скорость на бесконечно малом участке Δt в масштабе скоростей μ V.
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.250.169 (0.118 с.) |
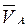 и
и 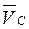 . Определить: скорости точек
. Определить: скорости точек 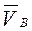 ,
,  ,
,  ; угловые скорости звеньев
; угловые скорости звеньев  ,
, 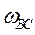 .
.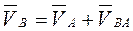 ;
;  (3.31)
(3.31)
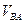 и
и  неизвестны по величине, но известны по направлению:
неизвестны по величине, но известны по направлению:  ;
;  .
. 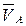 , определяем масштабный коэффициент
, определяем масштабный коэффициент .
.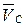
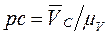 .
.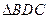 ~
~  ). Соединяем полюс с точкой d и определяем скорость точки D
). Соединяем полюс с точкой d и определяем скорость точки D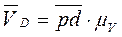
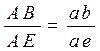 (3.32)
(3.32) (3.33)
(3.33)
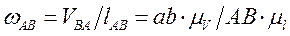
 (3.34)
(3.34) 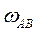 — угловая скорость звена АВ;
— угловая скорость звена АВ;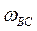 — угловая скорость звена ВС;
— угловая скорость звена ВС;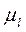 — масштабный коэффициент длин.
— масштабный коэффициент длин.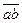 и
и  следует мысленно перенести в точку В плана механизма. Вектор относительной скорости
следует мысленно перенести в точку В плана механизма. Вектор относительной скорости 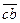 вращает звено ВС против часовой стрелки (см. рис. 3.7).
вращает звено ВС против часовой стрелки (см. рис. 3.7).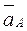 ,
, 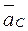 (рис. 3.8, а). Известны все скорости, т. к. план скоростей уже построен (см. рис. 3.7, б).
(рис. 3.8, а). Известны все скорости, т. к. план скоростей уже построен (см. рис. 3.7, б).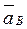 ,
, 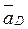 ,
,  ; угловые ускорения звеньев
; угловые ускорения звеньев 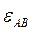 ,
, 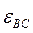 .
. ;
;  (3.35)
(3.35)  ,
, 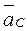 известны по величине и направлению. Величину векторов
известны по величине и направлению. Величину векторов 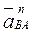 ,
,  можно определить, а направления их известны:
можно определить, а направления их известны: 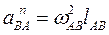 ; (вектор направлен от точки В к точке А);
; (вектор направлен от точки В к точке А);  (вектор направлен от точки В к точке С).
(вектор направлен от точки В к точке С).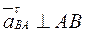 ,
, 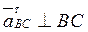 .
.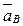 .
.
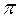 (рис. 3.8, б) откладывается в направлении вектора
(рис. 3.8, б) откладывается в направлении вектора 
 .
.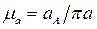 .
.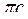
 , вектор πс направлен параллельно аС.
, вектор πс направлен параллельно аС. и
и 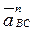 параллельно отрезкам АВ и ВС, соответственно.
параллельно отрезкам АВ и ВС, соответственно. ,
, 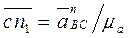 .
.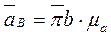
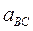 строится треугольник bdc подобный и сходственный с треугольником BDC. Находим ускорение точки D
строится треугольник bdc подобный и сходственный с треугольником BDC. Находим ускорение точки D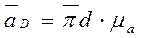
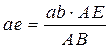 ,
,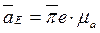
 ;
;  (3.36)
(3.36)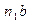 и nb с плана ускорений в точку В. Первый вектор вращает звено ВС против часовой стрелки, второй вращает звено АВ по часовой стрелке. Направления угловых ускорений показаны круговыми стрелками (см. рис. 3.8,а).
и nb с плана ускорений в точку В. Первый вектор вращает звено ВС против часовой стрелки, второй вращает звено АВ по часовой стрелке. Направления угловых ускорений показаны круговыми стрелками (см. рис. 3.8,а). .
.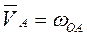 ;
;  .
. ;
; 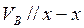 .
. .
. ; через полюс проводим направление абсолютной скорости точки В — горизонтальную прямую, параллельную х — х.
; через полюс проводим направление абсолютной скорости точки В — горизонтальную прямую, параллельную х — х.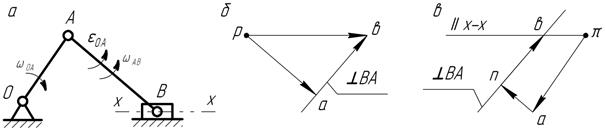
 .
. .
.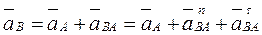
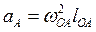 , вектор направлен от точки А к центру вращения – точке О.
, вектор направлен от точки А к центру вращения – точке О.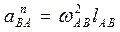 , вектор направлен от точки В к центру вращения – точке А.
, вектор направлен от точки В к центру вращения – точке А. .
. , правая часть уравнения изображена соответствующими векторами
, правая часть уравнения изображена соответствующими векторами 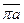 ,
,  ,
, 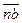 . Результирующий вектор
. Результирующий вектор 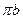 изображает абсолютное ускорение точки В.
изображает абсолютное ускорение точки В.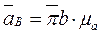
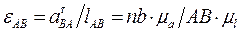
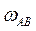 .
.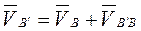
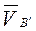 — скорость точки В', принадлежащей кулисе;
— скорость точки В', принадлежащей кулисе; — скорость точки В конца кривошипа и кулисного камня;
— скорость точки В конца кривошипа и кулисного камня;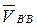 — относительная, скорость движения камня по кулисе.
— относительная, скорость движения камня по кулисе. ;
; 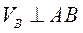
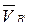 перпендикулярна кулисе DC;
перпендикулярна кулисе DC; 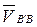 параллельна DC.
параллельна DC.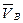 . Масштабный коэффициент плана скоростей
. Масштабный коэффициент плана скоростей  .
.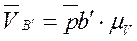
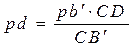 .
.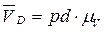 .
. определится из соотношения
определится из соотношения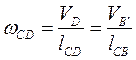
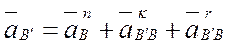
 - нормальное ускорение переносного движения (ускорение точки В конца кривошипа и кулисного камня). Вектор нормального ускорения направлен параллельно АВ от точки В к точке А. Откладываем в этом направлении отрезок произвольной величины (рис. 3.10, в) и определяем масштабный коэффициент плана ускорений
- нормальное ускорение переносного движения (ускорение точки В конца кривошипа и кулисного камня). Вектор нормального ускорения направлен параллельно АВ от точки В к точке А. Откладываем в этом направлении отрезок произвольной величины (рис. 3.10, в) и определяем масштабный коэффициент плана ускорений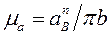
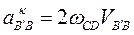 ,
,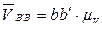 (см. рис. 3.10, б).
(см. рис. 3.10, б).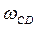 . Из точки b (рис. 3.10, б) откладываем
. Из точки b (рис. 3.10, б) откладываем 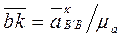
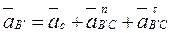
 , так как С — неподвижная точка, и ее ускорение изображается на плане нулевым отрезком (совпадает с полюсом).
, так как С — неподвижная точка, и ее ускорение изображается на плане нулевым отрезком (совпадает с полюсом).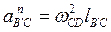 ; вектор направлен параллельно ВʹС.
; вектор направлен параллельно ВʹС.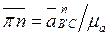 .
.
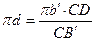 ;
; 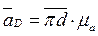 .
.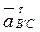 , которая на плане ускорений изображается отрезком
, которая на плане ускорений изображается отрезком 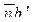
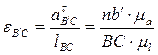
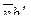
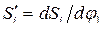 (3.37)
(3.37)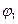 - обобщенная координата (угол поворота звена 1);
- обобщенная координата (угол поворота звена 1);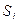 - перемещение точки i -ro звена.
- перемещение точки i -ro звена.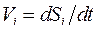 , поэтому
, поэтому (3.38)
(3.38)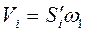 (3.39)
(3.39)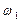 - угловая скорость начального звена.
- угловая скорость начального звена.  ; единица измерения аналога скорости - метр.
; единица измерения аналога скорости - метр.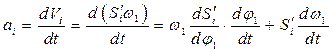 (3.40)
(3.40) (3.41)
(3.41)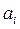 - ускорение точки i -го звена;
- ускорение точки i -го звена;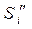 - аналог ускорения той же точки;
- аналог ускорения той же точки; - угловое ускорение начального звена.
- угловое ускорение начального звена.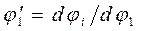 , (3.42)
, (3.42)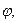 - угол поворота i -го звена.
- угол поворота i -го звена.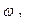 связана с ее аналогом соотношением:
связана с ее аналогом соотношением: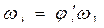 (3.43)
(3.43)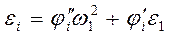 (3.44)
(3.44)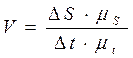 (3.45)
(3.45)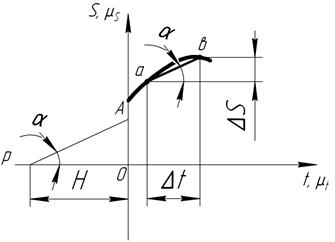
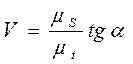 (3.46)
(3.46)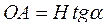 (3.47)
(3.47) (3.48)
(3.48)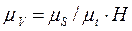 (3.49)
(3.49) 3.8. Метод кинематических диаграмм
3.8. Метод кинематических диаграмм


