
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитные колебания и волныСтр 1 из 6Следующая ⇒
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ Колебательный контур Простейший пример электрических колебаний – это колебания напряжения и тока в обычной осветительной сети. Эти колебания происходят в результате действия внешней ЭДС генератора, изменяющейся по синусоидальному закону, т.е. являются вынужденными колебаниями. Напомним, что колебания можно разделить на свободные и вынужденные. Вынужденные колебания – это колебания, происходящие при воздействии на колебательную систему какой-либо внешней периодически действующей силы. Свободные колебания возникают при смещении колебательной системы из положения равновесия (т.е. внешняя сила действует только один раз перед началом колебаний) и в дальнейшем происходят без каких-либо внешних периодических воздействий на маятник. Простейшие примеры механических систем, совершающих свободные колебания – пружинный и физический маятники. А могут ли электрические величины совершать свободные колебания?
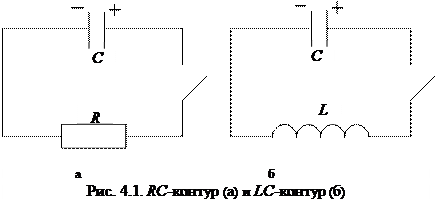
Рассмотрим схемы, представленные на рис. 4.1. Если заряженный до напряжения Качественно колебания в LC -контуре можно объяснить следующим образом. Главной причиной колебаний является ЭДС самоиндукции
Перед тем, как рассмотреть вопрос о колебаниях в LC -контуре количественно, вспомним некоторые определения и выводы, касающиеся гармонических колебаний и изложенные в первой части физики – механике. Колебания некоторой физической величины
где
Из последнего уравнения с учётом (4.1) следует
Соотношение (4.2) представляет собой дифференциальное уравнение гармонических колебаний. Мы показали, что если какая либо физическая величина совершает гармонические колебания, т.е. изменяется по закону (4.1), то для неё справедливо дифференциальное уравнение (4.2). В курсе дифференциальных уравнений доказывается и обратное утверждение: если для какой-либо физической величины удалось (используя законы физики) написать дифференциальное уравнение (4.2), то единственным его решением будет уравнение (4.1), т.е. величина
Теперь рассмотрим задачу о колебаниях в LC -контуре. В контуре действует единственная электродвижущая сила – ЭДС самоиндукции
По определению сила тока – это заряд, протекающий через сечение проводника за единицу времени, т.е. производная заряда по времени (см. формулу (2.1)). Если
Отметим, что в электротехнике величина ЭДС самоиндукции, взятая с обратным знаком, рассматривается как напряжение на катушке (индуктивности):
Уравнение (4.4) представляет собой, по сути, обобщение второго правила Кирхгофа, сформулированного нами ранее (см. п. 2.7) для замкнутых контуров с постоянными токами: сумма падений напряжений в замкнутом контуре равна алгебраической сумме внешних ЭДС, действующих в контуре. Внешние ЭДС в LC -контуре не действуют (ЭДС самоиндукции – это напряжение на индуктивности, внутренняя ЭДС). Разделив обе части уравнения (4.3) на величину
Уравнение (4.5) по форме совпадает с уравнением (4.2), т.е. является дифференциальным уравнением гармонических колебаний. Роль физической величины
во-вторых, квадрат циклической частоты колебаний (коэффициент при
Период колебаний связан с циклической частотой
Формула (4.8) для периода колебаний заряда в LC -контуре называется формулой Томсона. По гармоническому закону будут изменяться и другие физические величины, характеризующие процесс колебаний в LC -контуре. Зависимость напряжения на обкладках конденсатора от времени:
где Зависимость от времени силы тока найдется дифференцированием заряда по времени:
где
Сравнение последнего выражения с уравнением (4.6) показывает, что колебание тока отличается от колебания заряда (и напряжения) конденсатора по фазе на
Пример. 4.1. Максимальное значение напряжения на обкладках конденсатора LC -контура Решение. Задачу можно решить, используя уравнения колебаний напряжения и тока (4.9) и (4.10). Однако проще воспользоваться законом сохранения энергии. При колебаниях в LC -контуре энергия электрического поля конденсатора переходит в энергию магнитного поля катушки, и наоборот. Суммарная энергия электрического поля конденсатора и магнитного поля катушки в любой момент времени остаётся неизменной: В начальный момент времени напряжение на конденсаторе и его заряд максимальны. При этом сила тока в цепи равна нулю (рис. 4.2) и полный запас энергии контура состоит из энергии электрического поля конденсатора:
Метод векторных диаграмм
Закон Ома для амплитуд переменных токов внешне напоминает закон Ома для постоянного тока. А как выглядят законы последовательного и параллельного соединения элементов в цепи переменного тока? Как можно рассчитать токи и напряжения на отдельных элементах в случае разветвлённых цепей? Если два синусоидальных тока
Сложить два колебания одинаковой частоты можно, используя метод векторных диаграмм (рис. 4.8). В плоскости x 0 y из начала координат проводятся векторы, длины которых равны
и начальной фазой
Точно так же складываются напряжения при последовательном соединении элементов цепи. Итак, складывать токи и напряжения в цепи с переменным синусоидальным током нужно векторно. Законы для последовательного и параллельного соединения двух элементов можно записать в виде
Приведём несколько примеров.
Сначала ещё раз рассмотрим цепь, состоящую из активного сопротивления, индуктивности и ёмкости, соединённых последовательно (рис. 4.5). Пусть амплитуда силы тока в цепи равна
Вектор
Последняя формула в точности совпадает с формулой (4.23). Используя векторную диаграмму, легко найти сдвиг фаз между током в цепи и суммарным напряжением на концах цепи. Сдвиг фаз равен углу
Для нормального функционирования электрической схемы параметры всех её элементов должны быть точно рассчитаны. Как правило, расчёт электрических цепей с переменным током, содержит больше нюансов по сравнению со схемами питания постоянным током. Например, вблизи резонанса напряжение на отдельном элементе схемы может во много раз превышать амплитуду напряжения генератора.
Пример 4.5. Рассчитать допустимую амплитуду напряжения генератора Решение. Циклическая частота генератора
Полное сопротивление цепи
Для того, чтобы не было пробоя конденсатора, амплитуда напряжения на нём не должно превышать значение
Вывод: амплитуда напряжения генератора ~ 8 В приведёт к пробою конденсатора, выдерживающего напряжение 500 В! Пример 4.6. К генератору переменного синусоидального тока подключён резистор с сопротивлением
Решение. Соответствующие схемы представлены на рис. 4.10, а, б. Векторная диаграмма для схемы на рис. 4.10, а строится аналогично диаграмме на рис. 4.9. Вдоль оси 0 x отложим вектор амплитуда тока
Далее находим амплитуду силы тока
Так как по условию задачи
Поскольку в отсутствие катушки Теперь рассмотрим параллельное включение в цепь катушки (рис. 4.10,б). По закону параллельного соединения
Так как по условию задачи
из которого можно сделать вывод о том, что амплитуда силы тока генератора при параллельном включении в цепь катушки увеличится в
Электромагнитные волны
Волна – это процесс распространения колебаний в пространстве. В зависимости от природы волны колебания совершают различные физические величины. Например, в случае звуковых волн распространяются деформации в какой-то среде. Распространение волн происходит потому, что частицы среды связаны между собой упругими силами, способными вызывать колебания. Поэтому если сместить из положения равновесия какую-либо частицу среды, то начнет смещаться и соседняя частица и т. д. Вместе с колебаниями частиц колебания совершают плотность, давление, концентрация частиц в среде. Проще всего представить себе морские волны. Длиной волны (
Например, если за одну минуту (60 с) на берег приходит 10 волн, а расстояние между гребнями Примером электромагнитной волны является свет. Она представляет собой распространение в пространстве электрических и магнитных полей. Существование электромагнитных волн впервые теоретически предсказал Максвелл. Этот факт следует из его уравнений (см. п. 3.19). Изменяющееся (переменное) электрическое поле вызывает появление в окружающем пространстве изменяющегося магнитного поля. В свою очередь изменяющееся магнитное поле порождает изменяющееся электрическое поле и т. д. Таким образом, переменные электрическое и магнитное поля образуют электромагнитное поле, распространяющееся в пространстве. Так как существование электромагнитных волн никоим образом не связано со средой, они, в отличие от звуковых волн, могут распространяться в вакууме. Скорость распространения электромагнитных волн в вакууме или скорость света Электромагнитная волна является поперечной волной, т.е. колебания векторов напряженности электрического поля ( Конечно, когда мы смотрим на луч света, невозможно догадаться, что свет – волна, и тем более, электромагнитная волна. Огибающую векторов напряженностей полей мы не видим, и не можем «на глаз», как в случае морских волн, оценить длину волны. Экспериментальным доказательством волновой природы света являются опыты по интерференции и дифракции света, которые изучают в разделе «Оптика». А простейшим прибором для определения длины волны света является дифракционная решётка.
Итак, при распространении электромагнитной волны в каждой точке, через которую проходит волна, колебания совершают напряженности электрического и магнитного полей. Если колебания электрического вектора
Поскольку
Уравнение (4.33) называется уравнением линейно поляризованной волны или, сокращенно, уравнением плоской волны. Из уравнения (4.33) следует, что плоская волна представляет собой периодический процесс, как во времени, так и в пространстве. Если рассматривать какую-то фиксированную точку с координатой z 0, то слагаемое
где
В данном случае Пространственную и временную периодичность волн просто понять, рассматривая морские волны. Линия, огибающая поверхность моря в любой момент похожа на синусоиду – это пространственная периодичность. Если на море плавает чайка, то она движется вверх-вниз – это периодичность во времени. Шкала электромагнитных волн Электромагнитные волны могут иметь различные частоты и, соответственно, различные длины ( Волны с частотами менее 105 Гц (длинами волн более 3000 м) называются длинными волнами. Далее, радиоволны имеют частоты от 105 до 3·1010 Гц (длины волн от 3000 м до 1 см). Далее следует микроволновая область: частоты от 3·1010 до 6·1011 Гц (длины волн от 1 см до 0,5 мм). Источники излучения длинных волн, радиоволн и миллиметровых волн являются электрические токи в антеннах, электроны небольших энергий, движущиеся в электрических и магнитных полях. К микроволновой области примыкает диапазон инфракрасных волн: частоты от 6·1011 до 4,3·1014 Гц (длины волн от 0,5 мм до 0,76 мкм = 760 нм). Источниками излучения инфракрасных волн являются молекулы любого нагретого вещества. Например, инфракрасные волны излучают все окружающие нас тела при комнатной температуре. Электромагнитные волны с частотами от 4,3·1014 Гц до 7,6·1014 Гц (длинами волн от 760 нм до 380 нм) лежат в области чувствительности человеческого глаза, т.е. представляют собой видимый свет. Свет с длиной волны 760 нм, распространяющийся в вакууме, соответствует темно-красному цвету, а свет с длиной волны 380 нм – темно-фиолетовому. Отметим, что при переходе в достаточно плотные среды скорость световых волн и длина световой волны заметно изменяются, а частота волн остается без изменения. Отношение скорости света в вакууме к скорости света в среде называется абсолютным показателем преломления среды (точно также соотносятся и длины волн). За ощущение цвета ответственна частота волны. Поэтому, например, красный мяч останется красным, если его разглядывать под водой. Потом следуют ультрафиолетовые волны:частоты от 7,6·1014 Гц до 5·1016 Гц (длины волн от 380 нм до 6 нм). Источниками видимого и ультрафиолетового излучения являются атомы и молекулы, валентные электроны которых (электроны внешних орбиталей, расположенных далее всего от ядра) находятся в возбужденных состояниях, а также заряженные частицы высоких энергий.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.149 с.) |
||||||||||||||||||||||||||||||||||||||||||||
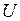 конденсатор емкостью
конденсатор емкостью 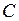 замкнуть на резистор, то конденсатор практически мгновенно разрядится (рис. 4.1,а). Энергия конденсатора по закону сохранения не исчезает бесследно. При протекании тока разрядки провод нагреется, т.е. весь запас энергии конденсатора перейдёт в тепло:
замкнуть на резистор, то конденсатор практически мгновенно разрядится (рис. 4.1,а). Энергия конденсатора по закону сохранения не исчезает бесследно. При протекании тока разрядки провод нагреется, т.е. весь запас энергии конденсатора перейдёт в тепло: 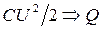 . Если же конденсатор замкнуть на катушку с индуктивностью
. Если же конденсатор замкнуть на катушку с индуктивностью  (рис. 4.1, б), то конденсатор будет не просто разряжаться, а перезаряжаться, т.е. в контуре возникнут колебания заряда на конденсаторе. А вместе с ними возникнут и колебания тока в контуре, напряжения на конденсаторе, ЭДС самоиндукции, возникающей в витках катушки, колебания энергий электрического поля конденсатора и магнитного поля катушки. Энергия электрического поля конденсатора будет переходить в энергию магнитного поля катушки, и наоборот
(рис. 4.1, б), то конденсатор будет не просто разряжаться, а перезаряжаться, т.е. в контуре возникнут колебания заряда на конденсаторе. А вместе с ними возникнут и колебания тока в контуре, напряжения на конденсаторе, ЭДС самоиндукции, возникающей в витках катушки, колебания энергий электрического поля конденсатора и магнитного поля катушки. Энергия электрического поля конденсатора будет переходить в энергию магнитного поля катушки, и наоборот 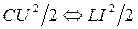 . Контур, состоящий из ёмкости и индуктивности, называется колебательным контуром без затухания (сопротивление контура
. Контур, состоящий из ёмкости и индуктивности, называется колебательным контуром без затухания (сопротивление контура 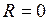 ) или LC -контуром. А сам колебательный процесс в LC- контуре называется электромагнитными колебаниями.
) или LC -контуром. А сам колебательный процесс в LC- контуре называется электромагнитными колебаниями.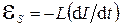 , возникающая в витках катушки при изменении тока. После замыкания цепи в контуре возникает электрический ток, направленный от положительной обкладки конденсатора к отрицательной. При этом ЭДС самоиндукции препятствует нарастанию тока, и он постепенно достигает своего наибольшего значения к тому моменту, когда конденсатор полностью разрядится. Так как в этот момент движущая сила (напряжение на конденсаторе) исчезла, ток начинает уменьшаться. Но, опять-таки, ток не может мгновенно уменьшится до нуля, поскольку теперь в витках катушки возникает ЭДС самоиндукции, препятствующая убыванию тока, т.е. некоторое время поддерживающая ток. За это время конденсатор успевает перезарядиться.
, возникающая в витках катушки при изменении тока. После замыкания цепи в контуре возникает электрический ток, направленный от положительной обкладки конденсатора к отрицательной. При этом ЭДС самоиндукции препятствует нарастанию тока, и он постепенно достигает своего наибольшего значения к тому моменту, когда конденсатор полностью разрядится. Так как в этот момент движущая сила (напряжение на конденсаторе) исчезла, ток начинает уменьшаться. Но, опять-таки, ток не может мгновенно уменьшится до нуля, поскольку теперь в витках катушки возникает ЭДС самоиндукции, препятствующая убыванию тока, т.е. некоторое время поддерживающая ток. За это время конденсатор успевает перезарядиться.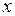 называются гармоническими, если она изменяется со временем по закону косинуса или синуса, т.е.:
называются гармоническими, если она изменяется со временем по закону косинуса или синуса, т.е.: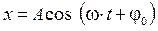 , (4.1)
, (4.1) - амплитуда колебаний (максимальное отклонение смещения
- амплитуда колебаний (максимальное отклонение смещения  - циклическая частота колебаний (
- циклическая частота колебаний (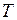 - период,
- период, 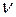 - частота колебаний);
- частота колебаний); 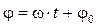 - фаза,
- фаза, 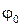 - начальная фаза колебаний. Первая и вторая производные величины
- начальная фаза колебаний. Первая и вторая производные величины 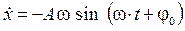 ,
,  .
. или:
или: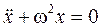 . (4.2)
. (4.2)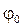 определяются начальными условиями, т.е. значениями величины
определяются начальными условиями, т.е. значениями величины 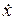 в начальный момент времени
в начальный момент времени 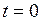 . Другими словами определяются тем, каким образом экспериментатор «запустит маятник».
. Другими словами определяются тем, каким образом экспериментатор «запустит маятник».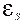 . Согласно закону Ома для неоднородного участка цепи, начало которого – положительная обкладка конденсатора, а конец – отрицательная (рис. 4.1,б), можно записать:
. Согласно закону Ома для неоднородного участка цепи, начало которого – положительная обкладка конденсатора, а конец – отрицательная (рис. 4.1,б), можно записать: 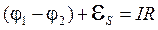 , где
, где 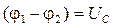 - разность потенциалов или напряжение между обкладками конденсатора. Так как сопротивление контура
- разность потенциалов или напряжение между обкладками конденсатора. Так как сопротивление контура 
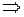
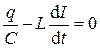 .
.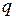 - это заряд положительной обкладки, то величина тока в контуре
- это заряд положительной обкладки, то величина тока в контуре 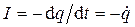 . Знак минус учитывает тот факт, что после замыкания ключа заряд положительной обкладки убывает (
. Знак минус учитывает тот факт, что после замыкания ключа заряд положительной обкладки убывает (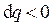 ). Тогда производная тока по времени есть вторая производная заряда по времени:
). Тогда производная тока по времени есть вторая производная заряда по времени:  . В результате получим:
. В результате получим: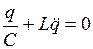 . (4.3)
. (4.3) . Поэтому уравнение (4.3) можно записать в виде
. Поэтому уравнение (4.3) можно записать в виде . (4.4)
. (4.4)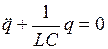 . (4.5)
. (4.5)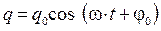 ; (4.6)
; (4.6) , откуда:
, откуда: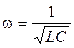 . (4.7)
. (4.7)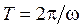 , тогда:
, тогда: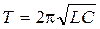 . (4.8)
. (4.8) , (4.9)
, (4.9)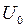 - максимальное напряжение или амплитуда напряжения на конденсаторе.
- максимальное напряжение или амплитуда напряжения на конденсаторе.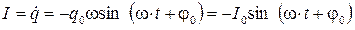 , (4.10)
, (4.10)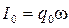 - максимальный ток в контуре или амплитуда тока. Воспользовавшись известной формулой тригонометрии
- максимальный ток в контуре или амплитуда тока. Воспользовавшись известной формулой тригонометрии  (формулой приведения), колебания тока можно записать через функцию косинус:
(формулой приведения), колебания тока можно записать через функцию косинус: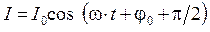 .
.
 . Это означает, что в тот момент, когда заряд конденсатора и напряжение на нём максимальны, т.е.
. Это означает, что в тот момент, когда заряд конденсатора и напряжение на нём максимальны, т.е. 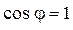 (напомним, что
(напомним, что 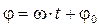 - фаза), ток в контуре равен нулю (если
- фаза), ток в контуре равен нулю (если 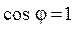 , то
, то 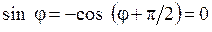 ). И, наоборот, когда ток максимален, заряд и напряжение на конденсаторе равны нулю. На рис. 4.2 показаны состояния LC -контура в моменты времени
). И, наоборот, когда ток максимален, заряд и напряжение на конденсаторе равны нулю. На рис. 4.2 показаны состояния LC -контура в моменты времени 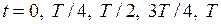 , где
, где 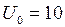 В. Определить значение силы тока
В. Определить значение силы тока 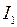 в контуре в тот момент, когда напряжение на конденсаторе станет равным
в контуре в тот момент, когда напряжение на конденсаторе станет равным 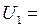 5 В, если
5 В, если 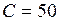 нФ,
нФ, 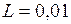 Гн.
Гн.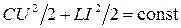 .
.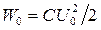 . В промежутке времени между
. В промежутке времени между 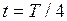 по цепи идёт ток, но конденсатор ещё полностью не разрядился. Поэтому энергия контура в конечный момент времени:
по цепи идёт ток, но конденсатор ещё полностью не разрядился. Поэтому энергия контура в конечный момент времени: 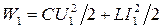 . Таким образом
. Таким образом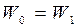
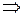
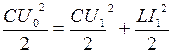
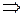
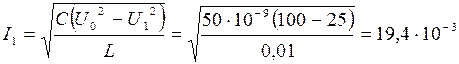 (А)
(А) 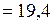 (мА).
(мА).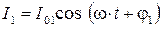 и
и 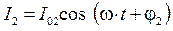 сходятся в узле, то суммарный ток, вытекающий из узла
сходятся в узле, то суммарный ток, вытекающий из узла 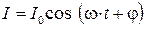 . Очевидно, что амплитуда суммарного тока в общем случае может быть не равна сумме амплитуд втекающих в узел токов:
. Очевидно, что амплитуда суммарного тока в общем случае может быть не равна сумме амплитуд втекающих в узел токов: 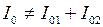 . Действительно, колебания токов
. Действительно, колебания токов 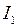 и
и 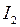 происходят с некоторой разностью фаз (величины
происходят с некоторой разностью фаз (величины 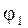 и
и 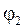 - разные), а значит, токи
- разные), а значит, токи 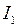 и
и 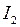 не одновременно достигают максимума или минимума.
не одновременно достигают максимума или минимума.
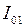 и
и 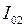 под углами
под углами 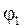 и
и  , а начальные фазы -
, а начальные фазы -  (4.25)
(4.25)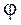 , определяемой из уравнения
, определяемой из уравнения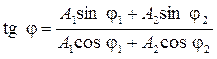 . (4.26)
. (4.26) и
и 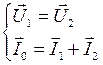 соответственно.
соответственно.
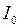 (сила тока будет одинакова для всех трёх элементов). Отложим вектор
(сила тока будет одинакова для всех трёх элементов). Отложим вектор  вдоль оси x (рис. 4.9). По закону Ома амплитуды напряжений на отдельных элементах цепи
вдоль оси x (рис. 4.9). По закону Ома амплитуды напряжений на отдельных элементах цепи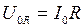 ,
, 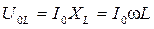 ,
, 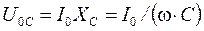 .
.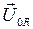 направлен вдоль оси 0 x так как напряжение на активном сопротивлении колеблется в одной фазе с током. Так как напряжение на индуктивности опережает ток по фазе на
направлен вдоль оси 0 x так как напряжение на активном сопротивлении колеблется в одной фазе с током. Так как напряжение на индуктивности опережает ток по фазе на  , вектор
, вектор 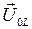 повёрнут относительно оси 0 x на угол
повёрнут относительно оси 0 x на угол  против часовой стрелки, т.е. направлен вдоль положительного направления оси 0 y. Так как напряжение на ёмкости отстаёт от тока по фазе на
против часовой стрелки, т.е. направлен вдоль положительного направления оси 0 y. Так как напряжение на ёмкости отстаёт от тока по фазе на 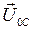 повёрнут относительно оси 0 x на угол
повёрнут относительно оси 0 x на угол 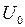 суммарного напряжения в цепи найдём из векторного уравнения:
суммарного напряжения в цепи найдём из векторного уравнения: 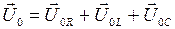 . Сначала удобно сложить противоположно направленные вектора
. Сначала удобно сложить противоположно направленные вектора 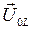 и
и 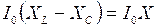 , где
, где 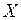 - реактивное сопротивление цепи. Далее по теореме Пифагора находим величину результирующего вектора
- реактивное сопротивление цепи. Далее по теореме Пифагора находим величину результирующего вектора 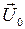

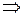
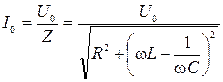 .
.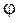 между векторами
между векторами 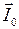 и
и 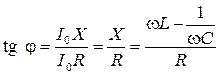 . (4.27)
. (4.27)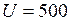 В. Параметры схемы:
В. Параметры схемы: 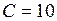 мкФ,
мкФ, 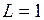 Гн,
Гн, 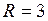 Ом, частота генератора
Ом, частота генератора 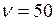 Гц.
Гц.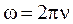 , индуктивное и ёмкостное сопротивления:
, индуктивное и ёмкостное сопротивления: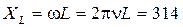 (Ом),
(Ом),  (Ом).
(Ом).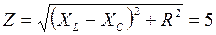 (Ом).
(Ом).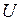 :
: 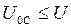 . Амплитуда напряжения на конденсаторе
. Амплитуда напряжения на конденсаторе 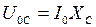 . По закону Ома (4.24) амплитуда тока в цепи
. По закону Ома (4.24) амплитуда тока в цепи 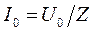 . Таким образом
. Таким образом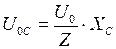
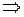

 ,
,  (В).
(В). . Во сколько раз изменится амплитуда силы тока генератора, если к резистору подключить катушку с индуктивным сопротивлением
. Во сколько раз изменится амплитуда силы тока генератора, если к резистору подключить катушку с индуктивным сопротивлением  а) последовательно, б) параллельно? Активным сопротивлением катушки пренебречь.
а) последовательно, б) параллельно? Активным сопротивлением катушки пренебречь.

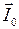 . Тогда вектора амплитуд напряжений
. Тогда вектора амплитуд напряжений 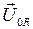 и
и 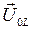 на сопротивлении
на сопротивлении 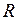 и индуктивности
и индуктивности 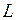 будут направлены вдоль осей 0 x и 0 y соответственно (рис. 4.11, а). Суммарное напряжение или амплитуду напряжения генератора
будут направлены вдоль осей 0 x и 0 y соответственно (рис. 4.11, а). Суммарное напряжение или амплитуду напряжения генератора 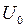 найдём по теореме Пифагора:
найдём по теореме Пифагора:
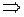
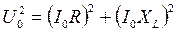 .
.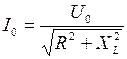 .
.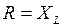 , получаем:
, получаем: .
.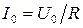 , можно сделать вывод о том, что амплитуда силы тока генератора при последовательном включении в цепь катушки уменьшится в
, можно сделать вывод о том, что амплитуда силы тока генератора при последовательном включении в цепь катушки уменьшится в  раз. Заметим, что если бы вместо индуктивности мы последовательно включили ещё одно такое же активное сопротивление
раз. Заметим, что если бы вместо индуктивности мы последовательно включили ещё одно такое же активное сопротивление 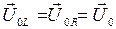 . При построении векторной диаграммы в этом случае удобно сначала отложить вектор амплитуды напряжения в цепи
. При построении векторной диаграммы в этом случае удобно сначала отложить вектор амплитуды напряжения в цепи 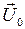 вдоль оси 0 x (рис. 4.11,б). Тогда, поскольку ток и напряжение на активном сопротивлении колеблются в одной фазе, вектор амплитуды силы тока
вдоль оси 0 x (рис. 4.11,б). Тогда, поскольку ток и напряжение на активном сопротивлении колеблются в одной фазе, вектор амплитуды силы тока 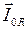 через сопротивление
через сопротивление 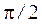 , вектор амплитуды силы тока
, вектор амплитуды силы тока 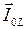 будет направлен антипараллельно оси 0 y. По закону параллельного соединения амплитуда суммарного тока генератора:
будет направлен антипараллельно оси 0 y. По закону параллельного соединения амплитуда суммарного тока генератора: 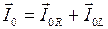 . Так как вектора
. Так как вектора 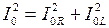 и с использованием закона Ома для отдельных участков цепи получаем
и с использованием закона Ома для отдельных участков цепи получаем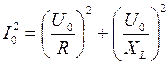
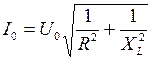 .
. ,
, ) называется расстояние между соседними гребнями (в случае звуковой волны – расстояние между ближайшими точками с максимальными плотностью или давлением). Эквивалентное определение: длина волны – это расстояние, которое волна проходит за время, равное периоду колебаний
) называется расстояние между соседними гребнями (в случае звуковой волны – расстояние между ближайшими точками с максимальными плотностью или давлением). Эквивалентное определение: длина волны – это расстояние, которое волна проходит за время, равное периоду колебаний 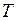 . В однородных средах волны распространяются с постоянной скоростью. Поэтому, исходя из определения длины волны, можно записать:
. В однородных средах волны распространяются с постоянной скоростью. Поэтому, исходя из определения длины волны, можно записать: 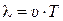 . Учитывая связь периода и частоты
. Учитывая связь периода и частоты 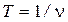 , получаем формулу, связывающую длину волны, скорость волны и частоту колебаний в волне любой природы:
, получаем формулу, связывающую длину волны, скорость волны и частоту колебаний в волне любой природы: . (4.32)
. (4.32)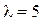 м, то частота
м, то частота 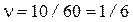 (Гц), а скорость волн
(Гц), а скорость волн 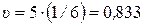 (м/с).
(м/с).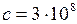 м/с. Ни один материальный объект в инерциальной системе отсчета не может иметь скорость большую, чем скорость света.
м/с. Ни один материальный объект в инерциальной системе отсчета не может иметь скорость большую, чем скорость света.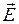 ) и магнитного поля (
) и магнитного поля (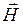 ) происходят перпендикулярно направлению распространения волны (рис. 4.12). При этом
) происходят перпендикулярно направлению распространения волны (рис. 4.12). При этом  .
.
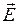 происходят все время параллельно какому-то одному направлению, то волна называется линейно поляризованной. При этом колебания вектора
происходят все время параллельно какому-то одному направлению, то волна называется линейно поляризованной. При этом колебания вектора 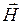 будут также происходить вдоль какого-то одного направления, поскольку
будут также происходить вдоль какого-то одного направления, поскольку 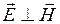 . На рис. 4.12 колебания вектора
. На рис. 4.12 колебания вектора 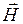 - вдоль оси y. Важным случаем электромагнитных волн является волна, в которой вектора
- вдоль оси y. Важным случаем электромагнитных волн является волна, в которой вектора 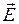 и
и 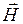 изменяются по гармоническому закону с какой-то циклической частотой
изменяются по гармоническому закону с какой-то циклической частотой 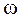 . Такая волна называется монохроматической. В этом случае для напряженности электрического поля в какой-то фиксированной точке пространства с координатой z можно записать
. Такая волна называется монохроматической. В этом случае для напряженности электрического поля в какой-то фиксированной точке пространства с координатой z можно записать 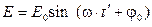 , где
, где 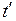 - время колебаний в точке с координатой
- время колебаний в точке с координатой 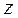 . Предположим, что в точке с координатой
. Предположим, что в точке с координатой 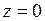 находится источник волны, тогда колебания в «нашей» точке
находится источник волны, тогда колебания в «нашей» точке 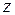 начнутся лишь через время
начнутся лишь через время 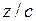 с момента начала распространения волны. Поэтому
с момента начала распространения волны. Поэтому 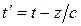 , где
, где  - время работы источника волны. Таким образом
- время работы источника волны. Таким образом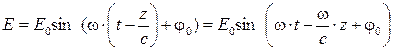 .
.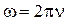 , а
, а 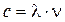 (см. 4.32), то
(см. 4.32), то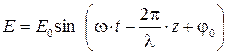 (4.33)
(4.33)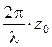 становится постоянным, и уравнение (4.33) для данной точки пространства
становится постоянным, и уравнение (4.33) для данной точки пространства ,
, - постоянная, играющая роль начальной фазы колебаний. Последнее уравнение показывает, что в любой фиксированной точке оси z 0 происходит периодический во времени процесс колебаний вектора напряженности электрического поля. Если зафиксировать какой-то момент времени
- постоянная, играющая роль начальной фазы колебаний. Последнее уравнение показывает, что в любой фиксированной точке оси z 0 происходит периодический во времени процесс колебаний вектора напряженности электрического поля. Если зафиксировать какой-то момент времени  , т.е. «заморозить волну» - «остановить» колебания векторов
, т.е. «заморозить волну» - «остановить» колебания векторов 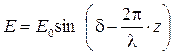 .
.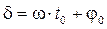 . Последнее уравнение указывает на пространственную периодичность плоской волны: огибающая всех векторов
. Последнее уравнение указывает на пространственную периодичность плоской волны: огибающая всех векторов 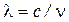 ). Классификация электромагнитных волн по частотам называется шкалой электромагнитных волн. Границы частот являются условными.
). Классификация электромагнитных волн по частотам называется шкалой электромагнитных волн. Границы частот являются условными.


