
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Матрицы и определители.
Действия над матрицами. Задача 1А. Найти сумму и разность матриц: Решение. Складываем поэлементно:
Вычитаем:
Ответ. Сумма: Задача 1Б. Найти сумму матриц: Решение. Складываем поэлементно:
Задача 2. Даны матрицы Найти Решение. Заметим, что размеры согласованы (2*3 и 3*2). Если первую разбить на строки, а вторую на столбцы, то видно, что есть всего 4 варианта скалярно умножить друг на друга вектор-строку их первой на вектор-столбец из второй.
Например, если умножаем строку номер 1 на столбец номер 2, то и число, которое при этом получается, ставим в 1 строку 2 столбец новой матрицы. Итак,
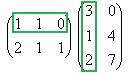
Теперь найдём Покажем, например, как 1-я строка скалярно умножается на 1-й столбец, они обведены.
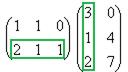
Ответ. Задача 3. Дана матрица Решение. Умножим матрицу саму на себя, то есть две её копии напишем рядом и умножим их.
Как видно из этого примера, для матриц, в отличие от чисел, возможно, что получается нулевой объект в ответе, притом что в исходной матрице вообще ни одного нуля не было. Это из-за особенностей её строения: правый столбец в 2 раза меньше, чем левый, а нижняя строка в минус 2 раза больше, чем верхняя. И вообще, если взять пару матриц, где у первой будет пропорциональность строк (в k раз больше) а у второй - столбцов (в минус k раз меньше) получим такой же эффект. Задача 4. Даны матрицы Решение.
Ответ.
Задача 5. Найти произведение матриц Решение. Размеры согласованы: длина строки 1-й матрицы равна высоте столбца 2-й матрицы. Первую можно мысленно разрезать на 2 строки, вторую на 3 столбца. Итого будет 6 различных произведений строк на столбцы.
* 20 минут - контр. задача № 2 (система уравнений в поле вычетов). Практика № 6. Задача 6. Вычислить Заметим, что получаются 1-й и 2-й столбец матрицы.
Замечание. При умножении квадратной матрицы на вектор-столбец получается снова вектор-столбец, то есть квадратная матрица фактически выступает в роли функции, отображающей векторы в пространстве (или на плоскости, если n = 2). Коротко о понятии линейного оператора и строении его матрицы и о том, что при умножении на i-й базисный вектор получается столбец номер i.
Задача 7А. Найти произведение: Задача 7Б. Решение. В 1-м случае размеры
Для пункта «Б» 1-я и 2-я строка умножаются не только на 1-й и 2-й, но ещё и на 3-й столбец. Дополнительно получаем
Выделим красным цветом новый столбец:
Ответ. 7А: Задача 8. Даны матрицы
Решение. Так как матрица С находится справа во всех слагаемых, то для удобства можно использовать приведение подобных Сначала запишем
Теперь умножим на матрицу С. Точно так же, как и в прошлом примере, мысленно обведём строку из 1-й матрицы на столбец из 2-й. Есть 4 варианта это сделать:
Ответ. Задача дом-1. Найти Задача дом-2. Ответ. Задача дом-3. Ответ. Задача 9. Дана матрица Решение. Сначала умножим две, и найдём
Теперь домножим ещё на одну матрицу А, чтобы найти
Ответ. Замечание. Несмотря на то, что в общем случае коммутативности по умножению матриц нет, но если матрица
Задача дом-4. Найти Задача 10. Найти произведение
Решение. Вычислим
Замечание. Если вычислять Определители. Задача 11.
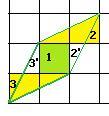
Для параллелограмма, построенного на базе системы векторов (2,1) и (1,2), площадь равна 3. Если область 2’ перенести в область 2, то видно, что получается половина прямоугольника площади 2 (выделено жёлтым). То есть площадь равна 1. Аналогично 3’ в 3. Там тоже площадь 1. Кроме того, в центре квадрат площади 1.
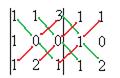
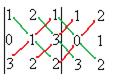
Задача 12. Найти определитель Решение. Ответ. 18. Задача 13. Найти определитель Решение. Допишем копии первых двух столбцов, проведём 3 параллельных линии (главная диагональ и ещё две). Перемножим все эти тройки элементов и внесём в общую сумму с их исходным знаком. А вот для побочной диагонали и линий, ей параллельных, со сменой знака.
Ответ.
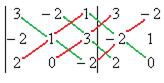
Задача 14. Найти определитель Решение.
То, что перемножено по зелёным линиям, включим в сумму со знаком плюс, а по красным - со знаком минус.
Ответ. 5. Задача 15. Найти определитель Решение.
Задача 16. Найти определитель Решение.
Задача 17. Вычислить определитель Решение. Заметим, что 1-й и 3-й столбец содержат очень похожие группы элементов а именно 1 и 2. Вычтем из 1-го столбца 3-й, а затем разложим по 1-му столбцу.
Задача 18 (с параметром). Найти параметр
Решение. Вычислим определитель и решим получившееся уравнение:
Ответ. Задача Дом-4. Вычислить определитель Задача дом-5. Вычислить определитель Задача дом-6. Найти определитель Задача дом-7. Найти параметр
Задача 19. Вычислить определитель Решение. Выберем дополняющий минор для каждого элемента 1-й строки, и домножим на
Замечание. Можно было из 2 столбца вычесть 1-й. Задача 20. Вычислить определитель Решение. Вычитаем из 2-й строки удвоенную 1-ю, и из 3-й 1-ю.
затем вычитаем из 3-й строки 2-ю. получили
Задача 21. Вычислить определитель Решение. Прибавим 1-ю строку ко 2-й, 3-й и 4-й.
Ответ. 24. Задача 22 (а,б). Вычислить определитель 4 порядка двумя способами: а) разложением по 1-й строке. б) с помощью преобразований матрицы.
Решение. Первый способ. Разложение по 1-й строке:
Очевидно, что последние 2 минора 3-го порядка вычислять не надо, так как они умножаются на 0. Осталось вычислить два минора 3 порядка, то есть мы свели определитель 4 порядка к определителям 3 порядка.
Ответ. 0. Второй способ. Из 2-го столбца вычтем 1-й
А теперь разложим по 1-й строке, причём реально для вычисления останется только один минор третьего порядка.
Ответ. 0. Задача дом-8. Вычислить определитель Задача 23. Вычислить определитель Решение. В последней строке, а также в последнем столбце, столбце видим 2 нуля и 2 ненулевых элемента. Можно сделать так, чтобы было 3 нулевых элемента. Прибавим удвоенную 3-ю строку ко 2-й:
Теперь можно от 3-го столбца отнять 2-й, умноженный на 8.
а далее разложить по последней строке:
вынесем общий множитель 4 из 1 столбца:
Задача 24. Доказать, что третий столбец матрицы является линейной комбинацией первых двух, и найти коэффициенты этой комбинации.
Решение. Во-первых, если вычислить определитель и обнаружить, что он равен 0, то этим самым уже доказана линейная зависимость столбцов. Однако требуется найти коэффициенты, поэтому запишем систему уравнений:
Прибавим удвоенное 1-е уравнение ко 2-му, и вычтем утроенное 1-е из 3-го.
Ответ. коэффициенты линейной комбинации равны 1 и 2. Замечание. ЛЗС образуют также и строки, из 1-й вычесть 2-ю = 3-я.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.218.147 (0.084 с.) |
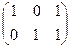 +
+ 
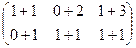 =
= 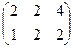 .
. =
=  .
.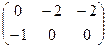 .
.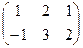 +
+ 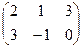
 =
= 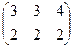 . Ответ.
. Ответ.  ,
,  .
.  и
и 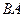 .
.
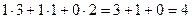





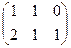
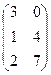 =
= 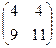 .
.  .
.


 .
. 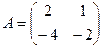 найти
найти  .
.
 =
= =
=  . Ответ.
. Ответ. 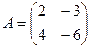
 . Найти
. Найти  .
.
 =
=  =
= 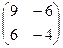
 =
= 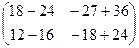 =
= 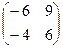 .
. .
. .
. =
=  . Ответ.
. Ответ. 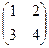
 и
и  .
.
 ,
,  .
.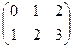
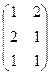 .
.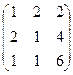 .
. и
и 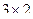 , согласованы, умножение возможно. Во 2-м случае
, согласованы, умножение возможно. Во 2-м случае  и
и  , тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.
, тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа. =
=  =
=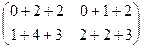 =
= 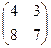 .
. =
=  =
= 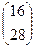 .
.
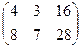 .
.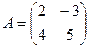 ,
, 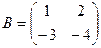 ,
, 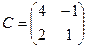 . Найти
. Найти  .
. 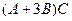 - тогда умножение надо будет проводить всего один раз, а не два.
- тогда умножение надо будет проводить всего один раз, а не два. .
.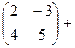
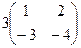 =
= 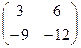 =
=  .
.

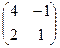 =
= 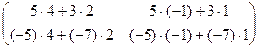 =
= 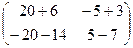 =
=  .
. 
 . Ответ.
. Ответ. 
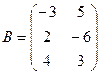 Найти
Найти  ,
,  .
.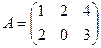
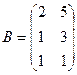 . Найти
. Найти  ,
, 
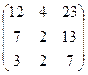 .
. . Найти
. Найти  .
.  .
.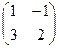
 =
= 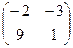 .
.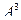 .
.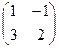 =
= 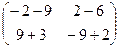 =
= 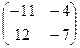 .
.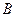 совпадает с матрицей
совпадает с матрицей  , тогда
, тогда 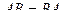 . Например, в этой задаче,
. Например, в этой задаче, 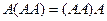 из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.
из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа. для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить
для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить 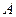 , либо взять
, либо взять  .
.  , где
, где ,
,  ,
, 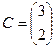 .
. , сначала умножим первые две матрицы:
, сначала умножим первые две матрицы:
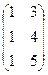 =
= 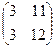 . Теперь умножим на третью матрицу.
. Теперь умножим на третью матрицу. =
= 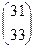 . Ответ.
. Ответ.  , то получается точно такой же результат, т.к. выполняется закон ассоциативности.
, то получается точно такой же результат, т.к. выполняется закон ассоциативности. 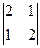 =
= 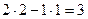 .
. 
 .
.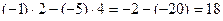 .
.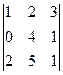

 =
=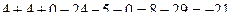 .
. .
. .
.
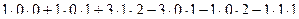 =
= 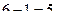 .
. .
. 
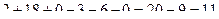 . Ответ. 11.
. Ответ. 11. 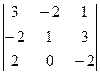 .
.
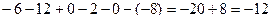 . Ответ.
. Ответ.  .
. .
. =
= 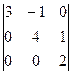 =
=  =
=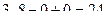 . Ответ. 24.
. Ответ. 24. , при котором определитель равен 0:
, при котором определитель равен 0: .
.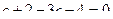 ,
,  ,
, 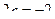 ,
,  .
. . Ответ. 28.
. Ответ. 28. . Ответ. 50.
. Ответ. 50. . Ответ.
. Ответ.  .
.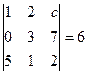 . Ответ. 4,2.
. Ответ. 4,2.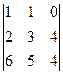 с помощью разложения по первой строке.
с помощью разложения по первой строке.
 =
=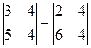 =
=  = 8. Ответ. 8.
= 8. Ответ. 8. методом Гаусса (приведением к треугольной форме).
методом Гаусса (приведением к треугольной форме).
 = 2. Ответ. 2.
= 2. Ответ. 2.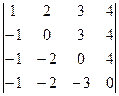 .
. . Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24.
. Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24. 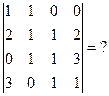

 =
= 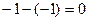 .
.
 . Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю.
. Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю. =
= 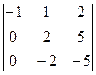 =
=  = 0.
= 0. . Ответ.
. Ответ.  .
. .
. =
= 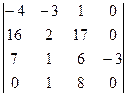 , теперь разложим по последнему столбцу, будет нужно вычислить всего 1 из 4 миноров порядка 4, так как остальные умножаются на 0.
, теперь разложим по последнему столбцу, будет нужно вычислить всего 1 из 4 миноров порядка 4, так как остальные умножаются на 0.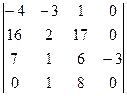 =
=  =
= 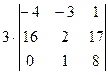 .
. =
= 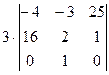
 =
=  ,
, =
= 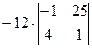 =
= 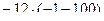 =
=  =
=  = 1212. Ответ. 1212.
= 1212. Ответ. 1212.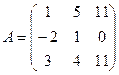

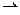

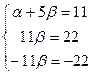 отсюда видно, что
отсюда видно, что 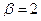 , тогда
, тогда  .
.


