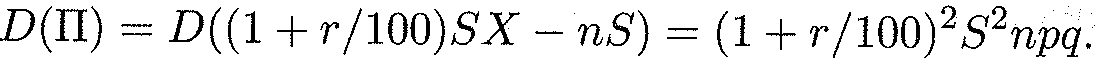Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики дискретной случайной величины.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности:
Из этого определения следует, что математическое ожидание есть некоторая постоянная (неслучайная) величина. Вероятностный же смысл математического ожидания состоит в том, что оно приближенно равно (особенно для большого числа испытаний) среднему арифметическому значений случайной величины. Это хорошо видно в случае, когда вероятности всех возможных значений дискретной случайной величины равны: pi - p = 1/n; из формулы (15.5) получаем
Пример 1. Найти математическое ожидание количества очков, выпадающих при бросании игральной кости. РЕШЕНИЕ. Выпадение каждой грани кубика от одного очка до шести имеет одинаковую вероятность р = 1/6. Следовательно, по формуле (15.6) получаем искомое математическое ожидание: М(Х) = (1 + 2 + 3 + 4 + 5 + 6)/6 = 3,5. Пример 2. Найти математическое ожидание числа невозврата кредитов по данным примера 4 п. 15.1. Решение. Воспользуемся итоговой таблицей распре деле ния дискретной случайной величины, полученной в этом примере, и формулой (15.6); находим М(Х) = 5 • 0,00032 + 4 • 0,0064 + 3 • 0,0512+ +2 • 0,2048 + 1 • 0,4096 + 0 • 0,32768 = 1. Свойства математического ожидания Математическое ожидание обладает рядом свойств, которые указаны ниже. Свойство 1. Математическое ожидание постоянной величины С равно этой постоянной: М(С) = С. Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = СМ(Х). Свойство 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: М(Х1 + Х2 + • • • + Хт) = М(Х 1) + М(Х2) + • • • + М(Хт). Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: М(Х 1 Х 2...Хт) = М(Х 1 )М(Х 2 )...М(Хт). Пример 3. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в некотором автосалоне составляют в среднем 100 тыс. р., а число продаж X автомашин в течение дня подчиняется следующему закону распределения: X 0 12 3 4 5 6 7 8 9 Р 0,25 0,2 0,1 0,1 0,1 0,1 0,05 0,05 0,025 0,025.. Так как то М(Х) = 0,2 +0,2 + 0,3 + 0,4 + 0,5 + 0,3 + 0,35 +0,2 + 0,0225 = 2,675 Найти математическое ожидание ежедневной прибыли при цене на машину 150 тыс. р.
Решение. Ежедневная прибыль подсчитывается по формуле П = (150Х — 100) тыс. р. Искомая характеристика М(П) находится с использованием указанных выше свойств математического ожидания (в тыс. р.): М(П)=М(150Х—100)=150М(Х) —100=150 • 2,675-100=301,25. Если в п независимых испытаниях вероятность появления в каждом из них события А постоянна, то ответ на вопрос о среднем числе появления события А дает следующая теорема. ТЕОРЕМА 15.1. Математическое ожидание М(Х) числа появлений события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: М(Х) = пр. (15.7) Пример 4 • Найти математическое ожидание числа выигрышных лотерейных билетов, если вероятность выигрыша по одному билету равна 0,015, причем куплено 200 билетов. Решение. Поскольку приобретение каждого билета является независимым испытанием относительно появления события А — выпадения выигрыша, то здесь применимы теорема 15.1 и формула (15.7). В нашем случае п = 200, р = 0,015, откуда мы получаем М (200) = 200 • 0,015 = 3.
Дисперсия дискретной случайной величины Как уже говорилось выше, математическое ожидание является средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые характеристики. Пусть X — случайная величина, а М (X) — ее математическое ожидание. Определение 2. Разность между случайной величиной и ее математическим ожиданием называется отклонением. Пусть закон распределения случайной величины X дается формулой (15.1), тогда отклонение Х—М(Х) имеет следующий закон распределения:
Отклонение имеет важное свойство, которое устанавливается непосредственно из свойств математического ожидания:
Пример 5. По данным примера 3 найти закон распределения отклонения числа проданных за день автомашин. Решение. Как было подсчитано в примере 3, М(Х) = 2,675. Тогда, согласно (15.8), искомый закон определяется следующей таблицей:
Определение 3. Математическое ожидание квадрата отклонения называется дисперсией или рассеянием: D (X) = M [ X - M (X)]2. (15.10) Пусть случайная величина задана законом распределения (15.1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения: [Х-М(Х)]2 [ x 1 –М(Х)]2 [х2-М(Х)]2... [хп-М(Х)]2 Р P 1 Р2. .. рп. Отсюда, согласно формуле (15.10), получаем формулу дисперсии в развернутом виде: D { X) = [ x 1 - M (X)]2 p 1 + [х2 - M (X)]2 p 2 +... + [хп - М(Х)]2рп. При вычислении дисперсии часто бывает удобно воспользоваться формулой, которая непосредственно выводится из формулы (15.10): D (X) = М(Х2) - [М(Х)]2. (15.11) Пример 6. Найти дисперсию ежедневной продажи числа автомашин по данным примера 3. Решение. Закон распределения случайной величины Х2 имеет вид X2 0 1 4 9 16 25 36 49 64 81 Р 0,25 0,2 0,1 0,1 0,1 0,1 0,05 0,05 0,025 0,025. Математическое ожидание М(Х2) подсчитывается из этой таблицы: М(Х2) = 0 • 0,25 + 1 • 0,2 + 4 • 0,1 + 9 • 0,1 + 16 • 0,1 + 25 ■ 0,1-1 +36 • 0,05 + 49 • 0,05 + 64 • 0,025 + 81 • 0,025 = 13,475. Математическое ожидание М(Х) = 2,675. Следовательно, согласно формуле (15.11), получаем искомую величину дисперсии: D (X) = М(Х2) - [М(Х)]2 = 13,475 - 7,156 = 6,319.
Свойства дисперсии Приведем здесь основные свойства дисперсии. Свойство 1. Дисперсия постоянной величины С равна, нулю: D (C) = 0. Свойство 2. Постоянный множитель можно выносить на знак дисперсии, возводя его в квадрат: D (CX) = C 2 D (X). (15.12) Свойство 3. Дисперсия алгебраической суммы независимых случайных величин равна сумме их дисперсий: D (X 1 + X 2 +... + Xn)= D (X 1)+ D (X 2)+... + D (Xn). Перечисленные свойства дисперсии используются при вычислениях, когда мы имеем дело с несколькими случайными величинами. Из свойств 1 и 3 следует важный вывод: D (X + С) = D (X), где С — постоянная величина. Кроме того, справедлива следующая теорема. ТЕОРЕМА 15.2. Дисперсия числа появления события А в п независимых испытаниях с вероятностью появления р в каждом из них этого события вычисляется по формуле D (X) = пр(1 - р) = npq. (15.14) Приведем здесь еще два важных результата: для случайной величины, распределенной по закону Пуассона ( Пример 7. Найти дисперсию числа выигрышных лотерейных билетов, если вероятность выигрыша по одному билету равна 0,015, причем куплено 200 билетов. Поскольку приобретение каждого билета является независимым испытанием относительно появления события А — выпадения выигрыша, то здесь применимы теорема 15.1 и формула (М(Х) = пр. 15.7). В нашем случае п = 200, р = 0,015, откуда мы получаем М (200) = 200 • 0,015 = 3. Решение. Имеем 200 независимых испытаний с вероятностью появления выигрышного билета р = 0,015. Стало быть, q = 1 — 0,015 = 0,985, откуда и получаем искомую дисперсию: D { X) = npq = 200 • 0,015 • 0,985 = 2,955. Пример 8. Банк выдал ссуды п разным заемщикам в размере S р. каждому под ставку ссудного процента r. Найти математическое ожидание и дисперсию прибыли банка, а также условие на ставку ссудного процента, если вероятность возврата ссуды заемщиком равна р.
Решение. Поскольку заемщики между собой не связаны, то можно полагать, что мы имеем п независимых испытаний. Вероятность утери ссуды для банка в каждом испытании равна q = 1 —р. Пусть X — число заемщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется формуле где X является случайной величиной с биномиальным законом распределения. Тогда, согласно теореме 15.1, математическое ожидание прибыли определяется с использованием фор мулы (15.7): М(П) = (1+г/100) SM (X) — nS = (1 + r /100) Snp — Sn = Sn (rp /100 - q). Поскольку выдача ссуды имеет смысл лишь при положительном математическом ожидании прибыли (положительная средняя величина прибыли), то из условия М( П) > 0 вытекает условие на ставку ссудного процента: г > 100 q / p, или г > 100(1 - р)/р. Дисперсия прибыли банка находится, согласно теореме 15.2, с использованием формулы (15.14) и свойств 1-3:
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.127.232 (0.018 с.) |
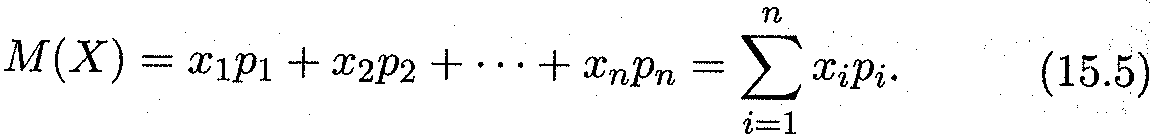
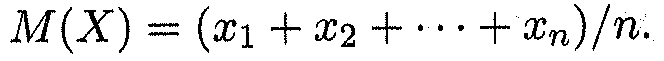 (15.6)
(15.6)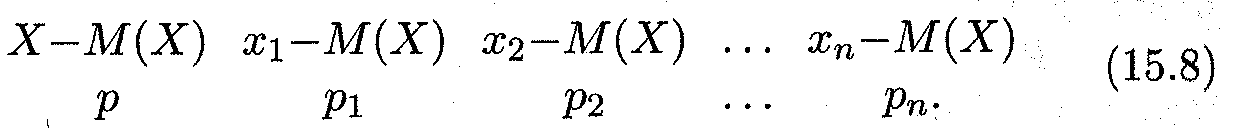
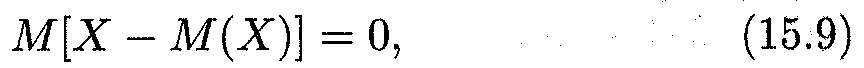 т.е. математическое ожидание отклонения равно нулю.
т.е. математическое ожидание отклонения равно нулю.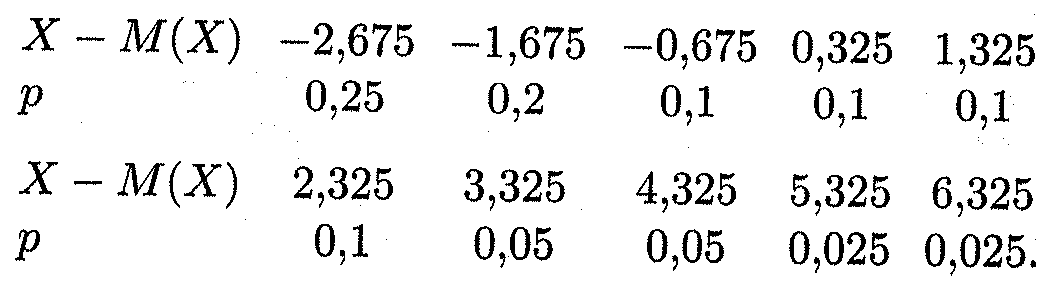 На практике важной характеристикой является рассеяние1 возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, согласно (15.9), равно нулю, так как суммируются отрицательные и положительные отклонения (см. пример 5), поэтому целесообразно ввести в рассмотрение абсолютные значения отклонений или их квадраты.
На практике важной характеристикой является рассеяние1 возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, согласно (15.9), равно нулю, так как суммируются отрицательные и положительные отклонения (см. пример 5), поэтому целесообразно ввести в рассмотрение абсолютные значения отклонений или их квадраты.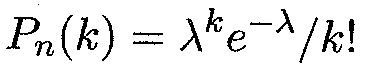 15.4 (пр = λ)), математическое ожидание и дисперсия равны параметру данного распределения.
15.4 (пр = λ)), математическое ожидание и дисперсия равны параметру данного распределения.