
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические действия над событиями.
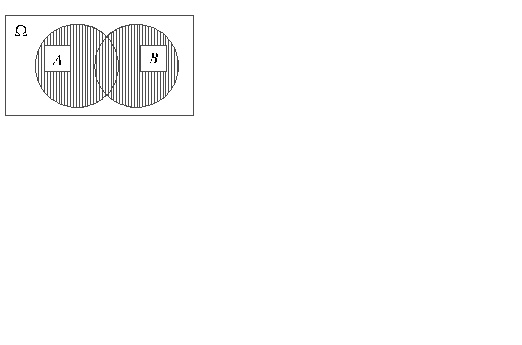
Суммой событий Приведем пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B - в том, что в мишень попадает 2-й. Событие С Аналогично суммой конечного числа событий А 1, А 2, ..., А k — называется событие А = А 1 + А 2 + ... + А k, состоящее в наступлении хотя бы одного из событий А i (i = 1, 2,..., k). Из определения следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А+ А = А (но не 2 А, как в алгебре). Произведением событий
На рисунке 3 пересечение событий А и B изображено в виде заштрихованной области. В условиях приведенного выше примера событие A•B заключается в том, что в мишень попали оба стрелка. Из определения следует, что АВ = ВА. Справедливы также сочетательный и дистрибутивный законы. Однако АА = А (но не А2). Элементы комбинаторики. Пусть дано множество, состоящее из n различных элементов. Размещением из n элементов по k Два размещения различны, если они отличаются друг от друга либо составом элементов, либо порядком их расположения. Число размещений из n элементов по k обозначают символом
где Пример 1. Составить различные размещения по два элемента из элементов множества А={3, 4, 5} и подсчитать их число. Решение. Из трех элементов можно образовать следующие размещения по два элемента:
Пример 2. Сколькими способами 3 награды (за 1-е, 2-е и 3-е места) могут быть распределены между 10 участниками соревнований? Решение. Будем считать, что каждый участник соревнований может получить не более одной награды. Выбрать 3-х участников из 10 можно следующим образом
Перестановкой из n элементов называется размещение из n элементов по n элементов. Число перестановок обозначается символом Pn и вычисляется по формуле: Таким образом, указать ту или иную перестановку из n элементов значит выбрать определенный порядок этих элементов. Поэтому любые две перестановки отличаются друг от друга только порядком следования элементов. Пример 3. Сколькими способами можно расставить на книжной полке десятитомник Д. Лондона, располагая их: 1) в произвольном порядке; 2) так, чтобы 1, 5 и 9 тома стояли рядом. Решение. 1) Число способов расстановки 10 книг равно числу перестановок из 10 элементов, то есть 2) Мысленно связав 1, 5 и 9 тома в одну связку, получим 8 «книг», то есть 7 книг и одну связку книг. Их можно расставить на полке Сочетанием из n элементов по k Любые два сочетания отличаются друг от друга хотя бы одним элементом (то есть отличаются только составом элементов). Число сочетаний из n элементов по k обозначается символом Для чисел
Пример 4. В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее: 1) 3 гвоздики; 2) 6 гвоздик одного цвета; 3) 4 красных и 3 розовых гвоздики. Решение. 1) Так как порядок выбора цветов не имеет значения, то выбрать 3 гвоздики из вазы, в которой стоят 16 гвоздик, можно 2) Выбрать 6 гвоздик красного цвета можно 3) Выбрать 4 красных гвоздик из 9 имеющихся можно
.4. Классическое и статистическое определение вероятности. Пусть производится опыт с n равновозможными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными событиями. Случай, который приводит к наступлению события А, называется благоприятным этому событию. Вероятностью события А называется отношение числа m исходов, благоприятствующих этому событию, к общему числу n исходов:
Из классического определения вероятности следуют следующие свойства: 1) вероятность достоверного события равна единице, то есть все исходы являются благоприятными (m = n): 2) вероятность невозможного события равна нулю (m =0): 3) вероятность случайного события есть положительное число, заключенное между нулем и единицей:
Статистическое определение вероятности связывает понятие вероятности с эмпирическим (опытным) понятием относительной частоты случайного события W (A), которая находится по результатам серии опытов. Относительной частотой случайного события А называется отношение числа опытов, в которых появилось данное событие na, к общему числу фактически произведенных опытов n: Статистической вероятностью события А называется постоянное число, к которому приближаются значения частоты этого события по мере увеличения числа опытов: Пример 5. В городе имеется одиннадцать различных коммерческих банков. Господин «N» открыл по одному счету в пяти различных банках. Позднее четыре банка из одиннадцати изменили ставки процентов по вкладам. Найти вероятность того, что по двум вкладам господина ставки остались неизменными. Решение. Господин выбирал банки случайным образом. Испытание – выбор пяти банков из имеющихся одиннадцати. A – событие, состоящее в том, что по двум вкладам господина, из имеющихся пяти, ставки остались неизменными, и, следовательно, по трем другим изменились.
Таким образом,
|
||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.96 (0.01 с.) |
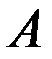 и
и 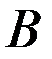 называется событие
называется событие 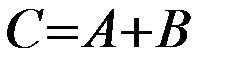 , которое происходит тогда и только тогда, когда происходит хотя бы одно из событий
, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий  означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.
означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.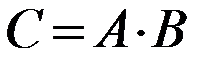 , которое происходит тогда и только тогда, когда происходят оба события
, которое происходит тогда и только тогда, когда происходят оба события 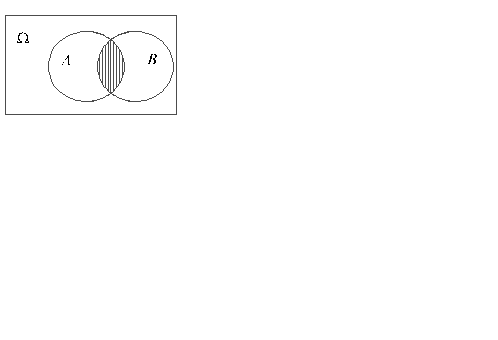
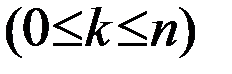 называется любое упорядоченное подмножество данного множества, содержащее k элементов.
называется любое упорядоченное подмножество данного множества, содержащее k элементов.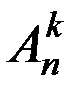 и вычисляют по формуле:
и вычисляют по формуле: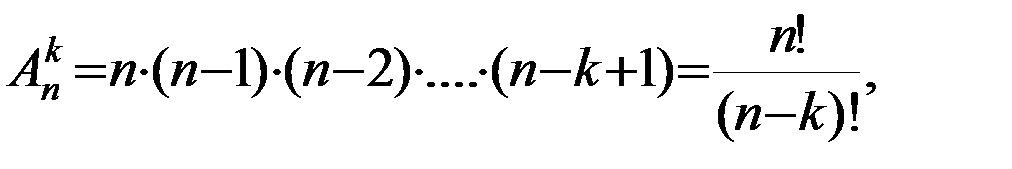
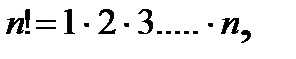 причем
причем 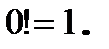
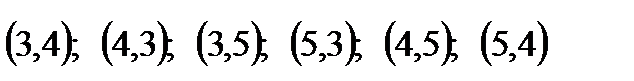 . Таким образом, всего их шесть. Однако число размещений можно посчитать и по формуле (1.1):
. Таким образом, всего их шесть. Однако число размещений можно посчитать и по формуле (1.1):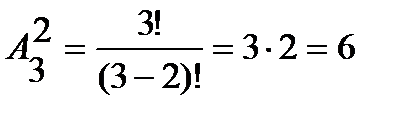 .
.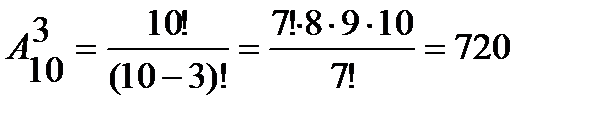 , так как «призовые тройки» отличаются друг от друга либо составом участников, либо порядком их следования.
, так как «призовые тройки» отличаются друг от друга либо составом участников, либо порядком их следования.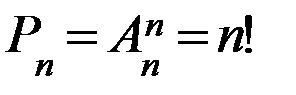
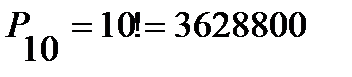 ;
; . Каждому из этих способов расстановки соответствуют
. Каждому из этих способов расстановки соответствуют 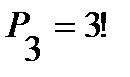 способов расстановки книг, находящихся в связке. Таким образом, число возможных расстановок 10 книг, чтобы три определенные книги стояли рядом (1, 5 и 9) равно:
способов расстановки книг, находящихся в связке. Таким образом, число возможных расстановок 10 книг, чтобы три определенные книги стояли рядом (1, 5 и 9) равно: 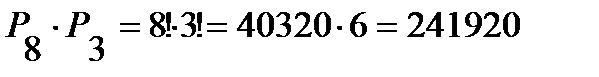 .
.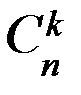 и вычисляется по формуле:
и вычисляется по формуле: 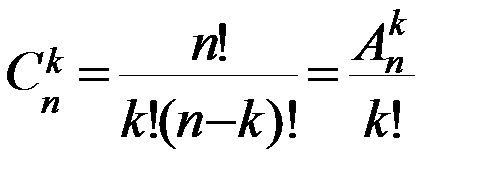
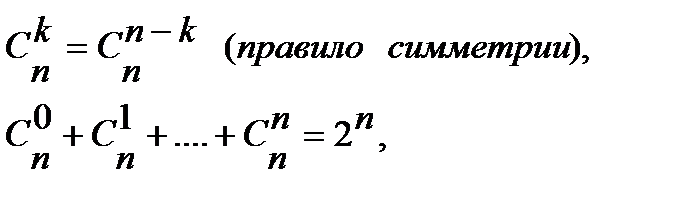
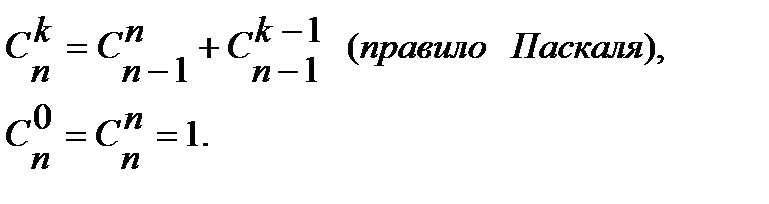
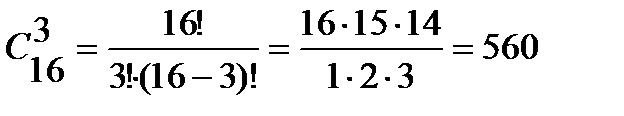 способами;
способами;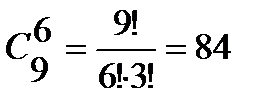 способами, а выбрать 6 гвоздик розового цвета можно
способами, а выбрать 6 гвоздик розового цвета можно  способами. По правилу сложения выбрать 6 гвоздик одного цвета (красных или розовых) можно
способами. По правилу сложения выбрать 6 гвоздик одного цвета (красных или розовых) можно 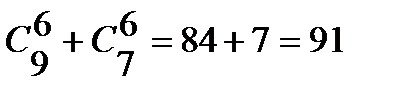 способом;
способом;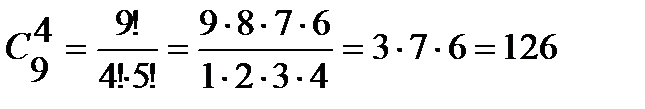 способами, а 3 розовых из имеющихся 7 можно
способами, а 3 розовых из имеющихся 7 можно 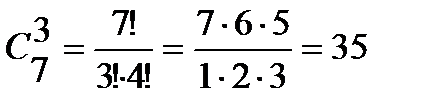 способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения
способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения 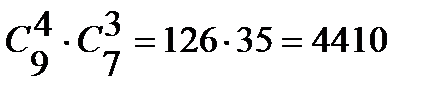 способами.
способами.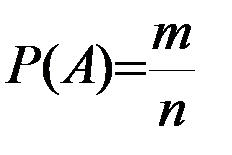
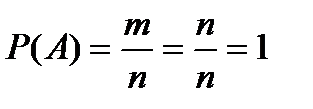 ;
;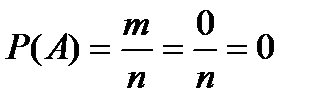 ;
;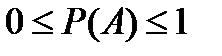 .
.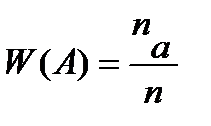 .
.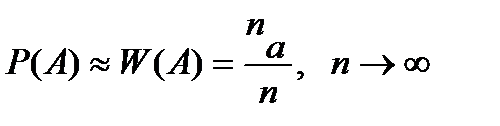
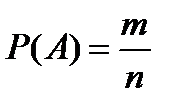 , где
, где 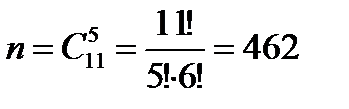 - число всех исходов испытания (несовместимых, единственно возможных и равновозможных);
- число всех исходов испытания (несовместимых, единственно возможных и равновозможных); 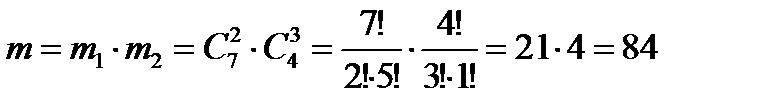 - число исходов, связанных с наступлением события А (
- число исходов, связанных с наступлением события А (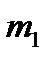 - число вариантов выбора двух банков, из имеющихся семи, не изменивших ставки процентов,
- число вариантов выбора двух банков, из имеющихся семи, не изменивших ставки процентов, 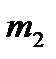 - число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).
- число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).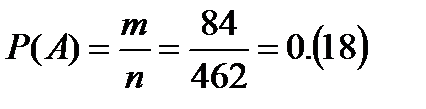 .
.


