
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многогранный угол. Трёхгранный уголСодержание книги Поиск на нашем сайте
Вариант 1 1. Плоские углы АMB и АMC трёхгранного угла MАBC соответственно равны 125° и 155°. Докажите, что плоский угол BMC меньше 80° и больше 30°. 2. Плоские углы АSB и АSC трёхгранного угла SАBC соответственно равны 30° и 45°. Двугранный угол при ребре SА равен 150°. Найдите плоский угол BSC. 3. Ребро BС тетраэдра PABC равно 8 см. Найдите расстояние от точки B до плоскости ACP, если Ð BCP = Ð ACP = 30°, cosÐ ACB = Вариант 2 1. Плоские углы АPB и BPC трёхгранного угла PАBC соответственно равны 110° и 165°. Докажите, что плоский угол АPC меньше 85° и больше 55°. 2. Плоские углы АMB и АMC трёхгранного угла MАBC соответственно равны 45° и 60°. Двугранный угол при ребре MА равен 30°. Найдите плоский угол BMC. 3. Ребро AС тетраэдра SАBC равно Вариант 3 1. Плоские углы CKB и АKC трёхгранного угла K АBC соответственно равны 115° и 160°. Докажите, что плоский угол АKB меньше 85° и больше 45°. 2. Плоские углы АPB и BPC трёхгранного угла PАBC соответственно равны 30° и 60°. Двугранный угол при ребре PB равен 120°. Найдите плоский угол АPC. 3. Ребро MС тетраэдра MАBC равно Вариант 4 1. Плоские углы АSB и АSC трёхгранного угла SАBC соответственно равны 130° и 170°. Докажите, что плоский угол BSC меньше 60° и больше 40°. 2. Плоские углы CKB и АKC трёхгранного угла K АBC соответственно равны 45° и 60°. Двугранный угол при ребре K C равен 150°. Найдите плоский угол АKB. 3. Ребро DC тетраэдра DАBC равно 20 см. Найдите расстояние от точки С до плоскости АDB, если Ð CDА = 30°, Ð АDB = 60°, cosÐ BDC = Самостоятельная работа № 18 Геометрическое место точек пространства Вариант 1 1. Длина отрезка АВ равна 10 см. Найдите геометрическое место точек Х, равноудалённых от точек А и В и таких, что АХ = 13 см. 2. Стороны АB, BC и АC треугольника АBC равны соответственно 15 см, 13 см и 4 см. Найдите геометрическое место точек Х таких, что каждая из прямых ХА, ХB и ХC образует с плоскостью АBC угол, равный 60°. 3. Найдите ГМТ, равноудалённых от пересекающихся плоскостей a и b и удалённых от плоскости a на 6 см. Вариант 2 1. Длина отрезка CD равна 12 см. Найдите геометрическое место точек Х, равноудалённых от точек C и D и таких, что CХ = 10 см.
2. Стороны АB, BC и АC треугольника АBC равны соответственно 17 см, 10 см и 9 см. Найдите геометрическое место точек Х таких, что каждая из прямых ХА, ХB и ХC образует с плоскостью АBC угол, равный 30°. 3. Найдите ГМТ, равноудалённых от пересекающихся плоскостей a и b и удалённых от их линии пересечения на 5 см. Вариант 3 1. Длина отрезка MK равна 16 см. Найдите геометрическое место точек Х, равноудалённых от точек M и K и таких, что KХ = 17 см. 2. Стороны АB, BC и АC треугольника АBC равны соответственно 20 см, 15 см и 7 см. Найдите геометрическое место точек Х таких, что каждая из прямых ХА, ХB и ХC образует с плоскостью АBC угол, равный 45°. 3. Найдите ГМТ, равноудалённых от пересекающихся плоскостей b и g и удалённых от плоскости g на 4 см. Вариант 4 1. Длина отрезка NP равна 24 см. Найдите геометрическое место точек Х, равноудалённых от точек N и P и таких, что PХ = 20 см. 2. Стороны АB, BC и АC треугольника АBC равны соответственно 20 см, 13 см и 11 см. Найдите геометрическое место точек Х таких, что каждая из прямых ХА, ХB и ХC образует с плоскостью АBC угол, равный 60°. 3. Найдите ГМТ, равноудалённых от пересекающихся плоскостей b и g и удалённых от их линии пересечения на 3 см. Самостоятельная работа № 19 Призма Вариант 1 1. Основанием прямой призмы является равнобокая трапеция, меньшее основание которой равно 8 см, а острый угол — 60°. Диагонали трапеции являются биссектрисами её острых углов. Найдите площадь боковой поверхности призмы, если её диагональ образует с плоскостью основания угол 30°. 2. Основанием наклонной призмы 3. Основанием прямой призмы Вариант 2 1. Основанием прямой призмы является равнобокая трапеция, основания которой равны 4 см и 12 см, а диагонали являются биссектрисами её тупых углов. Найдите площадь боковой поверхности призмы, если её диагональ образует с боковым ребром угол 30°. 2. Основанием наклонной призмы
3. Основанием прямой призмы Вариант 3 1. Основанием прямой призмы является равнобокая трапеция, основания которой равны 7 см и 17 см, а диагонали перпендикулярны. Найдите площадь боковой поверхности призмы, если её диагональ образует с плоскостью основания угол 45°. 2. Основанием наклонной призмы 3. Основанием прямой призмы Вариант 4 1. Основанием прямой призмы является равнобокая трапеция, большее основание которой равно 20 см, а острый угол — 60°. Меньшее основание трапеции равно её боковой стороне. Найдите площадь боковой поверхности призмы, если диагональ призмы образует с плоскостью основания угол 45°. 2. Основанием наклонной призмы 3. Основанием прямой призмы Самостоятельная работа № 20 Параллелепипед Вариант 1 1. Найдите диагональ прямоугольного параллелепипеда, если она больше его измерений на 10 см, 9 см и 1 см. 2. Стороны основания прямого параллелепипеда равны 16 см и 10 см, а острый угол — 60°. Найдите бóльшую диагональ параллелепипеда, если его высота равна 3. Основанием прямого параллелепипеда является ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны 6 см2 и 8 см2. Вариант 2 1. Найдите диагональ прямоугольного параллелепипеда, если она больше его измерений на 9 см, 8 см и 5 см. 2. Стороны основания прямого параллелепипеда равны 7 см и 3. Основанием прямого параллелепипеда является ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны 5 см2 и 12 см2. Вариант 3 1. Найдите диагональ прямоугольного параллелепипеда, если она больше его измерений на 16 см, 13 см и 5 см. 2. Стороны основания прямого параллелепипеда равны 5 см и 8 см, а острый угол — 60°. Найдите меньшую диагональ параллелепипеда, если его высота равна 24 см. 3. Основанием прямого параллелепипеда является ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны 15 см2 и 8 см2. Вариант 4 1. Найдите диагональ прямоугольного параллелепипеда, если она больше его измерений на 17 см, 13 см и 8 см.
2. Стороны основания прямого параллелепипеда равны 12 см и 3. Основанием прямого параллелепипеда является ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны 9 см2 и 12 см2. Самостоятельная работа № 21 Пирамида Вариант 1 1. Плоский угол при вершине правильной четырёхугольной пирамиды равен a. Найдите двугранный угол пирамиды при ребре основания. 2. Основанием пирамиды является равнобокая трапеция, основания которой равны 8 см и 4 см. Найдите площадь полной поверхности пирамиды, если каждый двугранный угол пирамиды при ребре основания равен 60°. 3. Основанием пирамиды является равносторонний треугольник, сторона которого равна 12 см. Каждая боковая грань образует с плоскостью основания угол, равный 30°. Найдите высоту пирамиды. Вариант 2 1. Двугранный угол правильной треугольной пирамиды при ребре основания равен a. Найдите плоский угол при вершине пирамиды. 2. Основанием пирамиды является прямоугольная трапеция, меньшая боковая сторона которой равна 10 см. Острый угол трапеции равен 30°. Найдите площадь полной поверхности пирамиды, если каждый двугранный угол пирамиды при ребре основания равен 45°. 3. Основанием пирамиды является равносторонний треугольник, сторона которого равна 24 см. Высота пирамиды равна Вариант 3 1. Угол между боковым ребром правильной четырёхугольной пирамиды и плоскостью основания равен a. Найдите плоский угол при вершине пирамиды. 2. Основанием пирамиды является равнобокая трапеция, боковая сторона которой равна 8 см, а острый угол — 60°. Найдите площадь полной поверхности пирамиды, если каждый двугранный угол пирамиды при ребре основания равен 30°. 3. Основанием пирамиды является равносторонний треугольник, сторона которого равна 18 см. Каждая боковая грань образует с плоскостью основания угол, равный 60°. Найдите высоту пирамиды. Вариант 4 1. Плоский угол при вершине правильной треугольной пирамиды равен a. Найдите двугранный угол пирамиды при ребре основания. 2. Основанием пирамиды является равнобокая трапеция, диагонали которой перпендикулярны, а боковая сторона равна 6 см. Найдите площадь полной поверхности пирамиды, если каждый двугранный угол пирамиды при ребре основания равен 45°. 3. Основанием пирамиды является равносторонний треугольник, сторона которого равна 6 см. Высота пирамиды равна 3 см. Все боковые грани образуют с плоскостью основания равные углы. Найдите эти углы.
Самостоятельная работа № 22 Усечённая пирамида Вариант 1 1. Стороны оснований правильной усечённой четырёхугольной пирамиды равны 10 см и 6 см, а боковое ребро образует с плоскостью большего основания угол 45°. Найдите площадь диагонального сечения усечённой пирамиды. 2. В правильной усечённой треугольной пирамиде стороны оснований равны 18 см и 36 см, а её высота — 3 см. Найдите площадь боковой поверхности усечённой пирамиды. 3. Все двугранные углы усечённой пирамиды при рёбрах большего основания равны 60°, а площади оснований равны 14 см2 и 36 см2. Найдите площадь боковой поверхности пирамиды. Вариант 2 1. Боковое ребро правильной усечённой четырёхугольной пирамиды равно 2. В правильной усечённой треугольной пирамиде стороны оснований равны 3. Площади оснований усечённой пирамиды равны 12 см2 и 28 см2, а площадь боковой поверхности — 32 см2. Все двугранные углы усечённой пирамиды при рёбрах большего основания равны. Найдите эти углы. Вариант 3 1. Сторона большего основания правильной усечённой четырёхугольной пирамиды равна 10 см, а высота пирамиды — 2. В правильной усечённой треугольной пирамиде стороны оснований равны 18 см и 6 см, а её высота — 2 см. Найдите площадь боковой поверхности усечённой пирамиды 3. Все двугранные углы усечённой пирамиды при ребрах большего основания равны 45°, а площади оснований равны 12 см2 и 40 см2. Найдите площадь боковой поверхности пирамиды. Вариант 4 1. Боковое ребро правильной усечённой четырёхугольной пирамиды равно 2. В правильной усечённой треугольной пирамиде стороны оснований равны 12 см и 42 см, а её высота — 5 см. Найдите площадь боковой поверхности усечённой пирамиды 3. Площади оснований усечённой пирамиды равны 20 см2 и 34 см2, а площадь боковой поверхности — Самостоятельная работа № 23 Тетраэдр Вариант 1 1. Плоскость пересекает рёбра АD, DB, BC и АC тетраэдра DАBC в точках M, N, K и F соответственно. Известно, что АM: MD = 2: 5, DN: NB = 3: 4, BK: KC = 5: 3. Найдите отношение АF: F C. 2. Найдите расстояние между серединами рёбер SА и BC ортоцентрического тетраэдра SАBC, если SА = 10 см, BC = 24 см. 3. Найдите медианы равногранного тетраэдра SАBC, если АB = 5 см, BC = 6 см, Вариант 2 1. Плоскость пересекает рёбра SB, SC, АC и АB тетраэдра SАBC в точках P, E, N и D соответственно. Известно, что BP: PS = 2: 1, SE: EC = 1: 4, CN: NА = 6: 5. Найдите отношение АD: DB.
2. Найдите расстояние между серединами рёбер АB и DC ортоцентрического тетраэдра DАBC, если АB = 16 см, DC = 30 см. 3. Найдите медианы равногранного тетраэдра DАBC, если АB = 5 см, DА = 4 см, Вариант 3 1. Плоскость пересекает рёбра АD, DC, BC и АB тетраэдра DАBC в точках E, K, P и M соответственно. Известно, что АE: ED = 3: 2, DK: KC = 4: 5, CP: PB = 5: 1. Найдите отношение АM: MB. 2. Найдите расстояние между серединами рёбер SB и АC ортоцентрического тетраэдра SАBC, если SА = 12 см, BC = 16 см. 3. Найдите медианы равногранного тетраэдра SАBC, если АS = 8 см, SC = 6 см, Вариант 4 1. Плоскость пересекает рёбра MC, MА, АB и BC тетраэдра MАBC в точках K, N, E и F соответственно. Известно, что CK: KM = 7: 3, MN: NА = 6: 5, АE: EB = 1: 7. Найдите отношение АD: DB. 2. Найдите расстояние между серединами рёбер АC и DB ортоцентрического тетраэдра DАBC, если АC = 20 см, DB = 21 см. 3. Найдите медианы равногранного тетраэдра DАBC, если BC = 7 см, CD = 9 см,
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 1306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.143.150 (0.011 с.) |

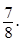
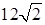 см. Найдите расстояние от точки A до плоскости SBC, если Ð SCА = Ð SCB = 45°, cosÐ ACB =
см. Найдите расстояние от точки A до плоскости SBC, если Ð SCА = Ð SCB = 45°, cosÐ ACB = 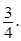
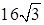 см. Найдите расстояние от точки С до плоскости АMB, если Ð CMB = Ð АMB = 60°, cosÐ АMC =
см. Найдите расстояние от точки С до плоскости АMB, если Ð CMB = Ð АMB = 60°, cosÐ АMC = 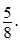
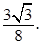
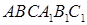 является равнобедренный треугольник ABC, в котором AB = AC = 10 см, BC = 16 см. Боковое ребро призмы
является равнобедренный треугольник ABC, в котором AB = AC = 10 см, BC = 16 см. Боковое ребро призмы 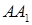 образует с плоскостью основания угол 30°, а проекцией вершины
образует с плоскостью основания угол 30°, а проекцией вершины 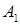 на плоскость ABC является середина отрезка BC. Найдите площадь грани
на плоскость ABC является середина отрезка BC. Найдите площадь грани 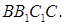
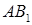 и
и 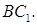
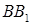 образует с плоскостью основания угол 45°, а проекцией точки
образует с плоскостью основания угол 45°, а проекцией точки 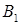 на плоскость ABC является точка пересечения медиан треугольника ABC. Найдите площадь грани
на плоскость ABC является точка пересечения медиан треугольника ABC. Найдите площадь грани 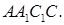
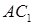 и
и 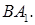
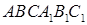 является прямоугольный треугольник ABC, в котором AC = BC = 4 см. Боковое ребро призмы
является прямоугольный треугольник ABC, в котором AC = BC = 4 см. Боковое ребро призмы 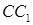 образует с плоскостью основания угол 60°, а проекцией точки
образует с плоскостью основания угол 60°, а проекцией точки 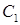 на плоскость ABC является центр описанной окружности треугольника ABC. Найдите площадь грани
на плоскость ABC является центр описанной окружности треугольника ABC. Найдите площадь грани 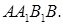
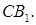
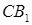 и
и 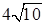 см.
см.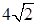 см, а острый угол — 45°. Найдите меньшую диагональ параллелепипеда, если его высота равна 12 см.
см, а острый угол — 45°. Найдите меньшую диагональ параллелепипеда, если его высота равна 12 см.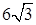 см, а острый угол — 30°. Найдите меньшую диагональ параллелепипеда, если его высота равна 8 см.
см, а острый угол — 30°. Найдите меньшую диагональ параллелепипеда, если его высота равна 8 см.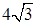 см. Все боковые грани образуют с плоскостью основания равные углы. Найдите эти углы.
см. Все боковые грани образуют с плоскостью основания равные углы. Найдите эти углы.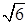 см, а сторона большего основания — 6 см. Найдите площадь диагонального сечения усечённой пирамиды, если её высота равна 2 см.
см, а сторона большего основания — 6 см. Найдите площадь диагонального сечения усечённой пирамиды, если её высота равна 2 см.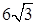 см и
см и 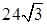 см, а её высота — 12 см. Найдите площадь боковой поверхности усечённой пирамиды.
см, а её высота — 12 см. Найдите площадь боковой поверхности усечённой пирамиды.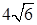 см. Боковое ребро пирамиды образует с плоскостью большего основания угол 60°. Найдите площадь диагонального сечения усечённой пирамиды.
см. Боковое ребро пирамиды образует с плоскостью большего основания угол 60°. Найдите площадь диагонального сечения усечённой пирамиды.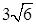 см, а сторона меньшего основания — 2 см. Найдите площадь диагонального сечения усечённой пирамиды, если её высота равна 6 см.
см, а сторона меньшего основания — 2 см. Найдите площадь диагонального сечения усечённой пирамиды, если её высота равна 6 см.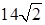 см2. Все двугранные углы усечённой пирамиды при рёбрах большего основания равны. Найдите эти углы.
см2. Все двугранные углы усечённой пирамиды при рёбрах большего основания равны. Найдите эти углы.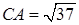 см.
см.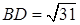 см.
см.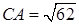 см.
см.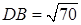 см.
см.


