
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двугранный угол. Угол между плоскостямиСодержание книги Поиск на нашем сайте
Вариант 1 1. В гранях двугранного угла проведены прямые a и b, параллельные его ребру, на расстоянии 10 см и 6 см от него соответственно. Найдите величину этого двугранного угла, если расстояние между прямыми a и b равно 14 см. 2. Из точек M и K, лежащих в разных гранях двугранного угла, величина которого равна 60°, проведены к его ребру перпендикуляры 3. Через гипотенузу АВ прямоугольного треугольника АВС проведена плоскость a. Катеты АС и ВС образуют с плоскостью a углы 30° и 45° соответственно. Найдите угол между плоскостями АВС и a. Вариант 2 1. В гранях двугранного угла проведены прямые m и n, параллельные его ребру, на расстоянии 8 см и 2. Из точек C и D, лежащих в разных гранях двугранного угла, величина которого равна 45°, проведены к его ребру перпендикуляры DA и CB. Найдите отрезок DC, если AB = 3 см, 3. Через гипотенузу АВ прямоугольного треугольника АВС проведена плоскость a. Угол между плоскостями АВС и a равен 60°, а катет АС образует с плоскостью a угол 30°. Найдите угол, который образует катет ВС с плоскостью a. Вариант 3 1. В гранях двугранного угла проведены прямые b и c, параллельные его ребру, на расстоянии 2. Из точек A и B, лежащих в разных гранях двугранного угла, величина которого равна 30°, проведены к его ребру перпендикуляры AC и B D. Найдите отрезок CD, если 3. Через гипотенузу АВ прямоугольного треугольника АВС проведена плоскость a. Катет АС образует с плоскостью a угол 45°, а угол АВС равен 60°. Найдите угол, который образует катет ВС с плоскостью a. Вариант 4 1. В гранях двугранного угла проведены прямые a и c, параллельные его ребру, на расстоянии 5 см и 8 см от него соответственно. Найдите величину этого двугранного угла, если расстояние между прямыми a и c равно 7 см. 2. Из точек D и E, лежащих в разных гранях двугранного угла, величина которого равна 120°, проведены к его ребру перпендикуляры 3. Через гипотенузу АВ прямоугольного треугольника АВС проведена плоскость a. Угол между плоскостями АВС и a равен 60°, а катет ВС образует с плоскостью a угол 45°. Найдите угол, который образует катет АС с плоскостью a. Самостоятельная работа № 15 Перпендикулярные плоскости Вариант 1 1. Точка S равноудалена от вершин квадрата ABCD. Точка O — её проекция на плоскость квадрата. Из точки S проведен перпендикуляр SM к стороне AB квадрата. Докажите, что плоскости ASB и OSM перпендикулярны. 2. Плоскости a и b перпендикулярны. Точки С и D принадлежат плоскости b. Прямая a принадлежит плоскости a и параллельна плоскости b. Из точек С и D к прямой a проведены перпендикуляры СA и DB. Известно, что DB = 17 см, а расстояния от точек С и D до линии пересечения плоскостей равны 6 см и 15 см соответственно. Найдите отрезок АС. 3. Плоскости прямоугольников ABCD и ABEF перпендикулярны. Найдите расстояние между прямыми DE и AB, если AF = 8 см, BC = 15 см (рис. 45).
Вариант 2 1. Точка M равноудалена от вершин C и D прямоугольника ABCD. Из точки M к стороне AB проведён перпендикуляр MN. Докажите, что плоскость прямоугольника перпендикулярна плоскости MNO, где O — точка пересечения диагоналей прямоугольника. 2. Плоскости b и g перпендикулярны. Точки A и B принадлежат плоскости g. Прямая c принадлежит плоскости b и параллельна плоскости g. Из точек A и B к прямой c проведены перпендикуляры AC и BD. Известно, что AC = 13 см, BD = 20 см, а расстояние от точки А до линии пересечения плоскостей равно 5 см. Найдите расстояние от точки B до линии пересечения плоскостей. 3. Плоскости квадратов ABCD и Вариант 3 1. Точка S равноудалена от вершин равностороннего треугольника ABC, точка O — центр этого треугольника. Докажите, что плоскость SOC перпендикулярна плоскости ASB. 2. Плоскости a и b перпендикулярны. Точки M и K принадлежат плоскости b. Прямая b принадлежит плоскости a и параллельна плоскости b. Из точек M и K к прямой b проведены перпендикуляры MF и KE. Известно, что KE = 20 см, а расстояния от точек M и K до линии пересечения плоскостей равны 9 см и 16 см соответственно. Найдите отрезок MF. 3. Плоскости прямоугольников AMND и BCNM перпендикулярны (рис. 47). Найдите расстояние между прямыми AC и MN, если AM = 2 см, MB = 3 см. Вариант 4 1. Точка P не принадлежит плоскости ромба ABCD и равноудалена от вершин В и D. Докажите, что плоскости АРС и ABC перпендикулярны. 2. Плоскости b и g перпендикулярны. Точки E и F принадлежат плоскости g. Прямая l принадлежит плоскости b и параллельна плоскости g. Из точек E и F к прямой l проведены перпендикуляры EK и FM. Известно, что EK = 17 см, FM = 25 см, а расстояние от точки F до линии пересечения плоскостей равно 20 см. Найдите расстояние от точки E до линии пересечения плоскостей. 3. Плоскости квадрата ABCD и прямоугольника Самостоятельная работа № 16
|
||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 1826; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.006 с.) |

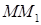 и
и 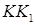 длиной 3 см и 8 см соответственно. Найдите отрезок MK, если
длиной 3 см и 8 см соответственно. Найдите отрезок MK, если 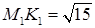 см.
см.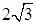 см от него соответственно. Найдите величину этого двугранного угла, если расстояние между прямыми m и n равно
см от него соответственно. Найдите величину этого двугранного угла, если расстояние между прямыми m и n равно 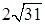 см.
см.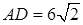 см, BC = 8 см.
см, BC = 8 см.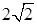 см и 4 см от него соответственно. Найдите величину этого двугранного угла, если расстояние между прямыми b и c равно
см и 4 см от него соответственно. Найдите величину этого двугранного угла, если расстояние между прямыми b и c равно 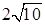 см.
см.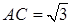 см, BD = 2 см,
см, BD = 2 см, 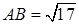 см.
см.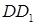 и
и 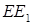 длиной 3 см и 5 см соответственно. Найдите отрезок DE, если
длиной 3 см и 5 см соответственно. Найдите отрезок DE, если 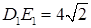 см.
см.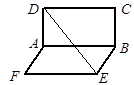
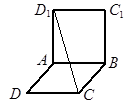
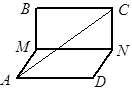
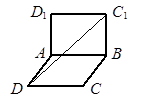
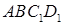 перпендикулярны (рис. 46). Найдите расстояние между прямыми
перпендикулярны (рис. 46). Найдите расстояние между прямыми 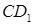 и AB, если AB = 6 см.
и AB, если AB = 6 см.


