
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь ортогональной проекции многоугольникаСодержание книги
Поиск на нашем сайте
Вариант 1 1. Ортогональной проекцией треугольника ABC на некоторую плоскость является прямоугольный треугольник 2. Треугольник 3. Грань АВCD прямоугольного параллелепипеда Вариант 2 1. Ортогональной проекцией треугольника ABC на некоторую плоскость является равносторонний треугольник 2. Треугольник 3. Грань АВCD прямоугольного параллелепипеда Вариант 3 1. Ортогональной проекцией треугольника ABC на некоторую плоскость является прямоугольный равнобедренный треугольник 2. Треугольник 3. Грань АВCD прямоугольного параллелепипеда Вариант 4 1. Ортогональной проекцией треугольника ABC на некоторую плоскость является равнобедренный треугольник
2. Треугольник 3. Грань АВ С D прямоугольного параллелепипеда Самостоятельная работа № 17
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 1287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.158 (0.008 с.) |

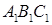 с гипотенузой 10 см и катетом 8 см. Найдите угол между плоскостями ABC и
с гипотенузой 10 см и катетом 8 см. Найдите угол между плоскостями ABC и 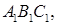 если площадь треугольника ABC равна
если площадь треугольника ABC равна 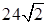 см2.
см2.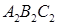 — ортогональная проекция треугольника
— ортогональная проекция треугольника 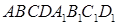 является квадратом, сторона которого равна 6 см, ребро АА 1 равно 8 см. На рёбрах АВ и AD отметили точки K и М соответственно так, что AK = АМ = 2 см. Найдите площадь сечения параллелепипеда плоскостью KМС 1.
является квадратом, сторона которого равна 6 см, ребро АА 1 равно 8 см. На рёбрах АВ и AD отметили точки K и М соответственно так, что AK = АМ = 2 см. Найдите площадь сечения параллелепипеда плоскостью KМС 1.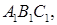 если площадь треугольника ABC равна 8 см2.
если площадь треугольника ABC равна 8 см2.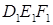 — ортогональная проекция треугольника DEF на плоскость a. Треугольник
— ортогональная проекция треугольника DEF на плоскость a. Треугольник 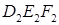 — ортогональная проекция треугольника
— ортогональная проекция треугольника 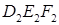 соответственно равны 42 см2 и 7 см2.
соответственно равны 42 см2 и 7 см2.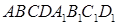 является квадратом, сторона которого равна 4 см, а ребро DD 1 равно 5 см. На рёбрах АD и DC отметили точки E и F соответственно так, что DE = DF = 1 см. Найдите площадь сечения параллелепипеда плоскостью EFB 1.
является квадратом, сторона которого равна 4 см, а ребро DD 1 равно 5 см. На рёбрах АD и DC отметили точки E и F соответственно так, что DE = DF = 1 см. Найдите площадь сечения параллелепипеда плоскостью EFB 1.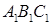 с гипотенузой 12 см. Найдите угол между плоскостями ABC и
с гипотенузой 12 см. Найдите угол между плоскостями ABC и 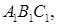 если площадь треугольника ABC равна 72 см2.
если площадь треугольника ABC равна 72 см2.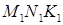 — ортогональная проекция треугольника MNK на плоскость a. Треугольник
— ортогональная проекция треугольника MNK на плоскость a. Треугольник 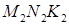 — ортогональная проекция треугольника
— ортогональная проекция треугольника 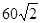 см2.
см2.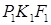 — ортогональная проекция треугольника PKF на плоскость b. Треугольник
— ортогональная проекция треугольника PKF на плоскость b. Треугольник 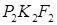 — ортогональная проекция треугольника
— ортогональная проекция треугольника 


