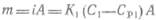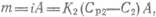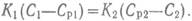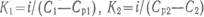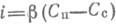Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы распространения теплоты в пространстве.Содержание книги
Поиск на нашем сайте
БИЛЕТ - 1 СПОСОБЫ РАСПРОСТРАНЕНИЯ ТЕПЛОТЫ В ПРОСТРАНСТВЕ. Самопроизвольный необратимый процесс переноса теплоты в пространстве с неоднородным распределением температуры называется теплообменом*. Теплообмен в общем случае может осуществляться тремя различными способами: теплопроводностью, конвекцией и тепловым излучением (радиацией). Теплопроводность (кондуктивный теплообмен) — это процесс распространения теплоты за счет непосредственного соприкосновения тел (частиц тела) друг с другом. Она обусловлена движением микрочастиц (молекул) тела и возможна в твердых, жидких и газообразных средах. Конвекция — это перенос теплоты движущимися макрообъемами жидкости или газа. Чем больше скорость движения среды, тем интенсивнее конвекция. Конвективный перенос теплоты всегда сопровождается теплопроводностью. Теплообмен, обусловленный совместным действием конвекции и теплопроводности, называется конвективным теплообменом. Тепловое излучение (радиация) — это распространение теплоты в пространстве посредством электромагнитных волн. Оно может происходить в вакууме, а также в средах, полностью или частично пропускающих излучение. При теплообмене излучением часть внутренней энергии излучателя превращается в энергию электромагнитных волн, которые распространяются в пространстве, а затем поглощается другим телом, превращаясь в тепловую. Совокупность трех перечисленных выше способов теплообмена называется сложным теплообменом. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Перенос теплоты, как всякое физическое явление, происходит в пространстве и во времени, поэтому температура в той или иной среде в общем случае зависит от координат рассматриваемой точки и времени: t = t (x, у, z, т). Совокупность мгновенных значений температуры в пространстве называется температурным полем. Если температурное поле во времени не изменяется, то оно называется стационарным, а если изменяется, то нестационарным. Тепловой режим, соответствующий стационарному температурному полю, называют установившимся, а тепловой режим, соответствующий нестационарному температурному полю, — неустановившимся. Если температура изменяется только вдоль одной координаты, то температурное поле называют одномерным, если вдоль двух координат — двумерным, вдоль трех — трехмерным. Различают также однородные и неоднородные температурные поля. В первом случае температура во всех точках температурного поля в каждый момент времени одна и та же, во втором — нет. В неоднородном температурном поле можно выделить точки с одинаковым значением температуры. Они образуют так называемую изотермическую поверхность. В неоднородном температурном поле возникает перенос теплоты — по одному или нескольким описанным выше механизмам (теплопроводность, конвекция, излучение). Количество теплоты, проходящее в единицу времени через произвольную поверхность, называют тепловым потоком Ф, Вт. Интенсивность переноса теплоты характеризуется поверхностной плотностью теплового потока, под которой понимают тепловой поток, равномерно распределенный на единице площади поверхности: q = Ф/А, Вт/м2, где А — площадь поверхности, через которую проходит тепловой поток Ф. Тепловой поток и плотность теплового потока могут быть выражены как в векторной, так и в скалярной форме. Под вектором плотности теплового потока понимают вектор, проекция которого на произвольное направление есть местная плотность теплового потока, проходящего через площадку, перпендикулярную к выбранному направлению. Распространение теплоты может происходить в какой-либо среде (твердой, жидкой, газообразной) или в вакууме. БИЛЕТ – 2 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕПЛООБМЕНА. СПОСОБЫ ТЕПЛООБМЕНА. КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ ПЕРЕНОСА ТЕПЛОТЫ. Самопроизвольный необратимый процесс переноса теплоты в пространстве с неоднородным распределением температуры называется теплообменом*. Теплообмен в общем случае может осуществляться тремя различными способами: теплопроводностью, конвекцией и тепловым излучением (радиацией). Теплопроводность (кондуктивный теплообмен) — это процесс распространения теплоты за счет непосредственного соприкосновения тел (частиц тела) друг с другом. Она обусловлена движением микрочастиц (молекул) тела и возможна в твердых, жидких и газообразных средах. Конвекция — это перенос теплоты движущимися макрообъемами жидкости или газа. Чем больше скорость движения среды, тем интенсивнее конвекция. Конвективный перенос теплоты всегда сопровождается теплопроводностью. Теплообмен, обусловленный совместным действием конвекции и теплопроводности, называется конвективным теплообменом. Тепловое излучение (радиация) — это распространение теплоты в пространстве посредством электромагнитных волн. Оно может происходить в вакууме, а также в средах, полностью или частично пропускающих излучение. При теплообмене излучением часть внутренней энергии излучателя превращается в энергию электромагнитных волн, которые распространяются в пространстве, а затем поглощается другим телом, превращаясь в тепловую. Совокупность трех перечисленных выше способов теплообмена называется сложным теплообменом. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Перенос теплоты, как всякое физическое явление, происходит в пространстве и во времени, поэтому температура в той или иной среде в общем случае зависит от координат рассматриваемой точки и времени: t = t (x, у, z, т). Совокупность мгновенных значений температуры в пространстве называется температурным полем. Если температурное поле во времени не изменяется, то оно называется стационарным, а если изменяется, то нестационарным. Тепловой режим, соответствующий стационарному температурному полю, называют установившимся, а тепловой режим, соответствующий нестационарному температурному полю, — неустановившимся. Если температура изменяется только вдоль одной координаты, то температурное поле называют одномерным, если вдоль двух координат — двумерным, вдоль трех — трехмерным. Различают также однородные и неоднородные температурные поля. В первом случае температура во всех точках температурного поля в каждый момент времени одна и та же, во втором — нет. В неоднородном температурном поле можно выделить точки с одинаковым значением температуры. Они образуют так называемую изотермическую поверхность. В неоднородном температурном поле возникает перенос теплоты — по одному или нескольким описанным выше механизмам (теплопроводность, конвекция, излучение). Количество теплоты, проходящее в единицу времени через произвольную поверхность, называют тепловым потоком Ф, Вт. Интенсивность переноса теплоты характеризуется поверхностной плотностью теплового потока, под которой понимают тепловой поток, равномерно распределенный на единице площади поверхности: q = Ф/А, Вт/м2, где А — площадь поверхности, через которую проходит тепловой поток Ф. Тепловой поток и плотность теплового потока могут быть выражены как в векторной, так и в скалярной форме. Под вектором плотности теплового потока понимают вектор, проекция которого на произвольное направление есть местная плотность теплового потока, проходящего через площадку, перпендикулярную к выбранному направлению. Распространение теплоты может происходить в какой-либо среде (твердой, жидкой, газообразной) или в вакууме. БИЛЕТ – 3 ЗАКОН ТЕПЛООТДАЧИ (ЗАКОН НЬЮТОНА-РИХМАНА). Для количественного описания теплоотдачи широко используется закон теплоотдачи, согласно которому плотность теплового потока, переносимого путем конвекции от поверхности теплообмена в среду (или, наоборот, из среды к поверхности теплообмена), пропорциональна разности температур поверхности теплообмена** (tc) и среды, (t ж), взятой по абсолютной величине:
где q — плотность теплового потока, Вт/м2. Коэффициент пропорциональности а в уравнении (10.1), имеющий размерность Вт/(м2-К), называется коэффициентом теплообмена***. Коэффициент теплообмена характеризует интенсивность теплоотдачи между поверхностью теплообмена и теплоносителем. Он равен плотности теплового потока1 (у поверхности теплообмена), отнесенной к температурному напору Дперепаду) между средой и поверхностью. * В теплотехнике жидкостью обычно называют как собственно капельную жидкость, так и газ. ** Поверхности стенки. *** Широко используется также термин «коэффициент теплоотдачи», Различают местный (локальный) коэффициент теплообмена, который относится к рассматриваемой точке поверхности теплообмена, и средний коэффициент теплообмена а, равный всему тепловому потоку Ф (Вт) через поверхность теплообмена А (м2). деленному на средний температурный напор Δ t ср и площадь поверхности теплообмена:
Коэффициент теплообмена — важный теплофизический параметр, необходимый для расчета теплообмен'ного аппарата. В общем случае он зависит от физических свойств жидкости, конфигурации и размеров поверхности теплообмена и от условий обтекания ее жидкостью. Коэффициент теплообмена — это расчетная величина, находимая обычно из уравнений, полученных экспериментально. ЗАКОН СТЕФАНА-БОЛЬЦМАНА. Из закона Планка путем интегрирования I λ 0 (λ) по длинам волн следует, что для абсолютно черного тела
где В технических расчетах закон Стефана — Больцмана обычно записывают в виде
где Для серых тел интенсивность излучения меньше, чем для абсолютно черного тела и, следовательно, Е<Ео. Отношение поверхностной плотности потока собственного интегрального излучения Е данного тела к поверхностной плотности потока интегрального излучения Ео абсолютно черного тела при той же температуре соответственно называют степенью черноты тела
где С= ε Со — коэффициент излучения серого тела. 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КОНВЕКТИВНОГО ТЕПЛООБМЕНА В подразделе 8.5 дан вывод дифференциального уравнения теплопроводности в неподвижной среде, аналогичным образом можно вывести дифференциальное уравнение в движущейся среде, называемое уравнением энергии, которое в декартовых координатах имеет вид
или в более краткой записи:
где τ — время, с; Vx, Vy, Vz — проекции вектора скорости на оси х, у, z, м/с; а — температуропроворности, м2/с;
полная производная температура по времени т, которую в связи с тем, что она связана с движущейся материей или субстанцией, называют субстанциальной производной и обозначают особым символом Dt / d τ;
Уравнение (10.3) описывает изменение температуры в точке х, у, z в неподвижной системе координат, при этом первый член левой части уравнения характеризует изменение температуры во времени, последующие члены левой части — изменение температуры вследствие движения жидкости через рассматриваемую точку пространства; правая часть уравнения выражает изменение температуры вследствие теплопроводности. При vx = vy = vz = 0 уравнение энергии переходит в дифференциальное уравнение теплопроводности (8.12). Для интегрирования уравнения (10.3) и расчета по нему температурного поля необходимо знать компоненты скорости vx, vy, vz. Это приводит в общем случае к необходимости дополнительного рассмотрения уравнений движения (уравнений Навье — Стокса) и уравнения неразрывности потока. Уравнения движения для несжимаемой жидкости (р = const) в проекциях на оси декартовых координат имеют вид: где р — плотность жидкости, кг/м3; gx, gy, gz — проекции ускорения поля внешних массовых сил на оси х, у. z. м/с2; р — давление. Па; р, — динамическая вязкость, Па-с; β — коэффициент объемного расширения, 1/К; tx — температура среды (температура жидкости в ядре потока);
С физической точки зрения уравнения (10.5) выражают равенство проекций равнодействующей всех сил, действующих на элемент объема жидкости (правые части уравнений), проекциям сил инерции (левые части уравнений). При этом первые слагаемые правых частей системы уравнений (10.5) выражают проекции подъемной силы, вторые слагаемые — проекции сил давления, третьи слагаемые — проекции сил внутреннего трения. Уравнение неразрывности для несжимаемых жидкостей записывается в виде Интегрирование системы уравнений (10.3), (10,5), (10.6) позволяет получить неизвестные функции t (x, у, z, τ), v { x, у, z, τ), р (x, y, z, τ). Для получения конкретного (частного) решения указанную систему уравнений необходимо дополнить условиями однозначности, которые, как и в случае интегрирования дифференциального уравнения теплопроводности (8.12), включают в себя геометрические, физические, начальные и граничные условия.
БИЛЕТ – 4 1. ТЕПЛОВАЯ ИЗОЛЯЦИЯ. ФИЗИЧЕСКИЙ СМЫСЛ ТЕПЛОПРОВОДНОСТИ λ На теплообменные поверхности с целью уменьшения тепловых потерь часто накладывается тепловая изоляция из материалов с низким значением теплопроводности λ.Материал считается теплоизоляционным, если его теплопроводность меньше0,2... 0,25 Вт/(м-К). Примерами теплоизоляционных материалов являются асбест, минеральная вата, диатомовый кирпич, пенопласт, пенобетон. Большинство теплоизоляционных материалов имеет пористое строение, поскольку воздух, заполняющий поры, сам по себе обладает малой теплопроводностью. Изготавливаются также вакуумно-многослойные и вакуумно-порошковые теплоизоляционные материалы, содержащие замкнутые вакуу-мированные поры, за счет чего создается низкая теплопроводность (эффективная теплоизоляция) порядка 10-4 Вт/(м-К). Наложение теплоизоляции на цилиндрическую поверхность имеет свою особенность: при увеличении толщины изоляции тепловой поток в одних случаях может уменьшаться, а в других — увеличиваться. Это происходит в силу того, что при утолщении изоляции наряду со снижением внутреннего термического сопротивления возрастает наружная поверхность теплообмена, что способствует увеличению теплопотерь. Анализ общего термического сопротивления двухслойной цилиндрической оболочки приводит к следующему выражению для так называемого критического диаметра изоляции d кр = 2 λ из / α 2, при котором имеют место максимальные теплапотери. При d из < d кр увеличение толщины изоляции приводит к увеличению теплопотерь, а при d из > d кр к их уменьшению. Поэтому при проектировании необходимо выбирать такой теплоизоляционный материал, для которого значение d кр меньше или равно наружному диаметру изолируемой трубы: dKP ≤ d 2. Решая это уравнение относительно искомого значения теплопроводности теплоизоляции, получим
БИЛЕТ - 5 БИЛЕТ – 6 БИЛЕТ – 7 МАССА И ТЕПЛОПЕРЕДАЧА. Рассмотрим массопередачу из одной фазы, другую через поверхность раздела фаз (рис. 14.3).
Пусть обе фазы являются двухкомпонентными; концентрация распределяемого компонента в ядре потока первой ф. а в ядре потока второй фазы С2. В состоянии термодинамического равновесия рассматриваемой системы температуры, давление и химические потенциалы компонентов обеих фаз равны: T 1 = Т2 При этом количество молекул распределяемого вещества, переходящее из фазы 1 в фазу 2, равно такому же их количество возвращающихся обратно за тот же промежуток времени и черту же поверхность контакта фаз, т. е. результирующий пси компонента равен нулю. Из-за различия физико-химических свойств фаз равновесии концентрации распределяемого компонента в фазах при этом (различны, но вполне определенны: каждой концентрации Ct соответствует своя, равновесная ей концентрация Ср2, и наоборот, концентрации С2 соответствует равновесная ей концентрация Сри т, е. при Т, р = const и C = var имеют место равновесные зависимости (концентрационные функции равновесия):
или
где т — количество распределяемого вещества, передаваемого из фазы в фазу 2 через поверхность раздела фаз А в единицу времени, кг/с; CP 1 и СР2 равновесные концентрации. Разности концентраций (С1 — CP 1) и (Ср2 — С2) в уравнениях (14.8) и (14.9) называют движущими силами массопередачи (соответственно по первой и второй фазам), которые берут по модулю (от большей концентрации вычитают меньшую). Коэффициенты пропорциональности K 1 и К2 в этих уравнениях — коэффициенты массопередачи: они связаны друг с другом соотношением
Размерность коэффициента массопередачи зависит от способа выражения концентраций: если концентрации выражены в кг/м3, am — в кг/с, то коэффициент массопередачи имеет размерность (м/с). С физической точки зрения коэффициент массопередачи выражает массу распределяемого компонента, прошедшего через единичную поверхность раздела фаз в единицу времени при движущей силе массопередачи, равной единице: БИЛЕТ – 8 МАССООТДАЧА. ЗАКОН МАССООТДАЧИ (ЗАКОН ЩУКАРЕВА). КОЭФФИЦИЕНТ МАССООБМЕНА. ЧИСЛА ПОДОБИЯ ПРИМЕНЯЕМЫЕ ПРИ РАСЧЕТЕ МАССООТДАЧИ. В движущейся среде масса переносится одновременно конвекцией (за счет движения самой среды) и диффузией. Массообмен, обусловленный совместным действием конвективного переноса вещества и молекулярной диффузии, носит название конвективного массообмена. В практических задачах большое значение имеет конвективный массообмен между жидкой или твердой поверхностью и окружающей средой. По аналогии с теплоотдачей конвективный массообмен между движущейся средой и поверхностью раздела с другой средой (твердым телом, жидкостью или газом) называют массоотдачей. Для количественного описания массоотдачи используется закон массоотдачи (закон Щукарева):
где i — плотность потока массы от поверхности раздела фаз в ядро потока (или наоборот), кг/(м2-с); Сп, Сс — концентрация распределяемого вещества у поверхности раздела фаз и в ядре потока (среды), соответственно, кг/м3 (рис. 14.2). При расчетах по уравнению (14.5) разность (Сп — Сс) всегда берется по модулю. Коэффициент пропорциональности р в уравнении (14.5) носит название коэффициента массообмена***, он пя.чномепность м/с и выражает собой массу, прошедшую в единицу времени через единицу поверхности контакта фаз при разности концентраций (Сп — Сс), равной единице: β — i (Сп - Сс).
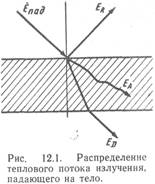
БИЛЕТ – 9 ЛУЧИСТЫЙ ТЕПЛООБМЕН. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. Основные понятия и определения. Тепловое излучение представляет собой процесс превращения внутренней энергии излучающего тела в лучистую энергию электромагнитных колебаний. При попадании лучистой энергии на другое тело она частично поглощается им, превращаясь во внутреннюю энергию. Особенность теплообмена излучением заключается в том, что отпадает необходимость в непосредственном контакте тел. Излучение электромагнитных волн свойственно всем телам. Излучение обладает как волновыми, так и корпускулярными свойствами, а именно — непрерывностью электромагнитных волн и дискретностью, характерной для испускаемых частиц — фотонов. Распространение излучения в пространстве определяется
волновыми свойствами, а энергия излучения — корпускулярными. Тепловое излучение характеризуется длиной волны λ и частотой колебаний v. При этом между ними имеется зависимость v = C / λ, где С = З*108 м/с — скорость распространения света. Излучение всех зависит от температуры. С увеличением темпе
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.199.240 (0.009 с.) |

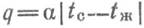
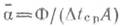
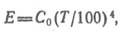
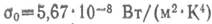 — постоянная Стефана — Больцмана (константа излучения абсолютно черного тела).
— постоянная Стефана — Больцмана (константа излучения абсолютно черного тела).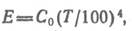
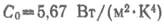 — коэффициент излучения абсолютно черного тела.
— коэффициент излучения абсолютно черного тела.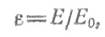 где ε <1 Плотность потока излучения Е находят по уравнению
где ε <1 Плотность потока излучения Е находят по уравнению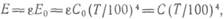
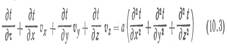
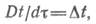
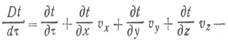
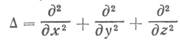 — оператор Лапласа.
— оператор Лапласа.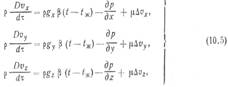
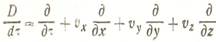 — — субстанциальная производная;
— — субстанциальная производная;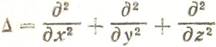 - оператор Лапласа.
- оператор Лапласа.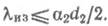

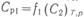
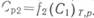 . На рисунке 14.4
. На рисунке 14.4 .Для описания массопередачи используют уравнение массопередачи, согласно которому количество вещества, передаваемого из одной фазы в другую в единицу времени, прямо пропорционально поверхности раздела фаз и разности концентраций (фактической и равновесной), взятой по концентрации распределяемого вещества в другой фазе. Поскольку в массопередаче участвуют две фазы, то уравнение массопередачи можно записать по одной или другой фазе, например при d > CPi:
.Для описания массопередачи используют уравнение массопередачи, согласно которому количество вещества, передаваемого из одной фазы в другую в единицу времени, прямо пропорционально поверхности раздела фаз и разности концентраций (фактической и равновесной), взятой по концентрации распределяемого вещества в другой фазе. Поскольку в массопередаче участвуют две фазы, то уравнение массопередачи можно записать по одной или другой фазе, например при d > CPi: