
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон теплопроводности (закон Фурье).
Основной закон теплопроводности (закон Фурье) устанавливает количественную взаимосвязь между тепловым потоком, вызванным теплопроводностью, и температурными неод-нородностями в среде. Для его формулировки выделим в среде изотермические поверхности со значениями температуры. Возьмем на изотермической поверхности некоторую точку Р. Проведем из точки Р нормаль п к изотермической поверхности. Под градиентом температуры понимают вектор, в направлении нормали к изотермической поверхности в сторону увеличения температуры и численно равный частной производной от температуры по этому направлению:
где 1гс — единичный вектор, направленный по нормали п в сторону возрастания температуры. Согласно основному закону теплопроводности плотность теплового потока прямо пропорциональна градиенту температуры:
где λ — коэффициент пропорциональности, называемый теплопроводностью, Вт/См-К). Скалярная запись уравнения (8.2) имеет вид
Знак минус в уравнениях (8.2) и (8.3) отражает разнона-правленность векторов grad t и q: вектор grad t по определению направлен в сторону возрастания температуры, а вектор q — • в сторону ее убывания. Выразим из (8.3) теплопроводность
Анализируя (8.4), можно установить физический смысл теплопроводности %: теплопроводность — это количество теплоты, проходящее в единицу времени через единицу изотермической поверхности при градиенте температуры, равном единице. БИЛЕТ – 15 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КОНВЕКТИВНОГО ТЕПЛООБМЕНА В подразделе 8.5 дан вывод дифференциального уравнения теплопроводности в неподвижной среде, аналогичным образом можно вывести дифференциальное уравнение в движущейся среде, называемое уравнением энергии, которое в декартовых координатах имеет вид
или в более краткой записи:
где τ — время, с; Vx, Vy, Vz — проекции вектора скорости на оси х, у, z, м/с; а — температуропроворности, м2/с;
полная производная температура по времени т, которую в связи с тем, что она связана с движущейся материей или субстанцией, называют субстанциальной производной и обозначают особым символом Dt / d τ;
Уравнение (10.3) описывает изменение температуры в точке х, у, z в неподвижной системе координат, при этом первый член левой части уравнения характеризует изменение температуры во времени, последующие члены левой части — изменение температуры вследствие движения жидкости через рассматриваемую точку пространства; правая часть уравнения выражает изменение температуры вследствие теплопроводности. При vx = vy = vz = 0 уравнение энергии переходит в дифференциальное уравнение теплопроводности (8.12). Для интегрирования уравнения (10.3) и расчета по нему температурного поля необходимо знать компоненты скорости vx, vy, vz. Это приводит в общем случае к необходимости дополнительного рассмотрения уравнений движения (уравнений Навье — Стокса) и уравнения неразрывности потока. Уравнения движения для несжимаемой жидкости (р = const) в проекциях на оси декартовых координат имеют вид: где р — плотность жидкости, кг/м3; gx, gy, gz — проекции ускорения поля внешних массовых сил на оси х, у. z. м/с2; р — давление. Па; р, — динамическая вязкость, Па-с; β — коэффициент объемного расширения, 1/К; tx — температура среды (температура жидкости в ядре потока);
С физической точки зрения уравнения (10.5) выражают равенство проекций равнодействующей всех сил, действующих на элемент объема жидкости (правые части уравнений), проекциям сил инерции (левые части уравнений). При этом первые слагаемые правых частей системы уравнений (10.5) выражают проекции подъемной силы, вторые слагаемые — проекции сил давления, третьи слагаемые — проекции сил внутреннего трения. Уравнение неразрывности для несжимаемых жидкостей записывается в виде Интегрирование системы уравнений (10.3), (10,5), (10.6) позволяет получить неизвестные функции t (x, у, z, τ), v { x, у, z, τ), р (x, y, z, τ). Для получения конкретного (частного) решения указанную систему уравнений необходимо дополнить условиями однозначности, которые, как и в случае интегрирования дифференциального уравнения теплопроводности (8.12), включают в себя геометрические, физические, начальные и граничные условия.
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.006 с.) |


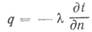
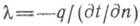
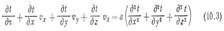


 — оператор Лапласа.
— оператор Лапласа.
 — — субстанциальная производная;
— — субстанциальная производная;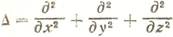 - оператор Лапласа.
- оператор Лапласа.


