
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О нелинейной регрессии и инструментальных переменных
Иногда линейная модель регрессии бывает недостаточной, с точки зрения её качества и значимости, тогда могут быть использованы нелинейные модели. В простейшей форме нелинейность может быть учтена путем введения инструментальных переменных zj = φ j (xj), которые входят в модель регрессии обычным линейным образом. Например, нелинейная модель 2-го порядка может быть построена следующим образом (рис. 5.4):
где
Рис.5.4 Кривая нелинейной среднеквадратической регрессии 2-го порядка
Часто в качестве инструментальных переменных используются степенная функция Таким образом, замена или введение новых переменных в регрессионную модель - это задача исследователя в конкретной предметной области деятельности. Числовой пример (часть 6) Опишем введение нелинейности в модель через инструментальные переменные в нашем сквозном примере. Для этого, построим графически корреляционное поле в плоскостях
Поэтому ввёдем вместо переменной
Эта модель уже нелинейная, но строится обычным образом после преобразования входных данных, при этом коэффициент детерминации повышается от 0.919 до 0.928. В нашем примере это повышение незначительное, но подобные преобразования могут привести и к серьёзному улучшению качества регрессионной модели.
Задачи факторного анализа В предыдущих главах рассматривались статистические данные, полученные в наблюдениях за величинами характеристик объектов при помощи того или иного измерительного прибора-инструмента. Такие данные объединялись в матрицу измерения Х, а наблюдаемые величины называли измеримыми факторами. Однако в наблюдениях часто замечено, что при анализе данных имеются некоторые непосредственно не измеримые, но весьма важные факторы, объясняющие наблюдаемые явления. Эти скрытые (латентные) факторы являются или причиной наблюдаемых измерений, или их обобщением. Например, такие понятия, как надёжность изделия или конструкции, её экономичность, экологичность или эргономичность неизмеримы непосредственно, но они связаны с измерениями величин предельно допустимых нагрузок, вибро-шумовых величин, химического состава, величин калибровочных настроек приборов и многого другого. Другой пример следующий, студенческая зачетная книжка есть матрица измерений его знаний, но она есть отражение других, скрытых факторов, таких как способность, усидчивость, мотивируемость, здоровье, склонности к точным, естественным или гуманитарно-художественным видам деятельности. Возникает вопрос, как методами статистического анализа данных измерений выделить и вычислить эти скрытые общие факторы, а также объяснить ими наблюдаемые измеримые факторы. Кроме того, желательно иметь весьма ограниченный набор таких общих факторов, который бы объяснял наблюдения с достаточно хорошей точностью. Мы будем строить факторную модель следующего вида [1,2]:
Здесь
Линейная факторная модель Наиболее простой и популярной факторной моделью является линейная факторная модель
Каждый измеримый j -фактор представляется в модели суммой линейной общефакторной части В матричной форме модель по всем измерениям измеримых факторов выглядит следующим образом:
где
Поскольку через вводимые общие факторы мы хотим линейно объяснять все измеримые факторы, то будем требовать от этих факторов (вернее их значений) выполнения условий теоремы Гаусса-Маркова, а именно: 1. 2. 3. 4.
5. Кроме того, будем требовать от модели также некоррелируемость общих факторов Как же ввести общие факторы в наблюдаемый нами массив измерений? Для понимания главной идеи факторного анализа вернёмся к задаче парного регрессионного анализа. Построим для корреляционного поля
Рис. 6.1. Идея построения новых факторов (главных координат) путем вращения измеримых факторов.
В новой системе координат
Угол Наиболее известно построение многомерной линейной факторной модели методом главных координат.
Метод главных координат В основе метода главных координат лежит линейное преобразование поворота измеренных величин
Матрица поворота должна обладать рядом свойств, обеспечивающих выполнение требований Гаусса-Маркова к линейной факторной модели. Для этого матрица поворота должна быть [9]: - ортогональной - преобразование вращения должно диагонализировать корреляционную матрицу в новой системе координат. Рассмотрим преобразование корреляционной матрицы: пусть
Построим матрицу поворота так, чтобы корреляционная матрица
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.197 (0.18 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

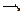

 ,
,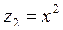 - инструментальная переменная.
- инструментальная переменная.
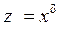 , логарифмическая
, логарифмическая 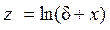 , показательная
, показательная  и иногда тригонометрическая
и иногда тригонометрическая 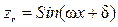 для выявления циклических факторов в зависимостях. Введение новых членов в модель регрессии, в том числе и инструментальных, оправдано тогда, когда возрастает качество регрессии. Например, значимо повышается коэффициент детерминации, ликвидируется мультиколлинеарность переменных, и т.д.
для выявления циклических факторов в зависимостях. Введение новых членов в модель регрессии, в том числе и инструментальных, оправдано тогда, когда возрастает качество регрессии. Например, значимо повышается коэффициент детерминации, ликвидируется мультиколлинеарность переменных, и т.д.  и проанализируем расположение на них точек измерений. Можно заметить по тесноте точек, что зависимость измерений объясняемой переменной
и проанализируем расположение на них точек измерений. Можно заметить по тесноте точек, что зависимость измерений объясняемой переменной 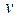 от переменной
от переменной 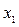 очень слаба в отличие от других трёх переменных. Кроме того, видно, что расположение точек на плоскости
очень слаба в отличие от других трёх переменных. Кроме того, видно, что расположение точек на плоскости  группируется не вдоль прямой линии, как на плоскости
группируется не вдоль прямой линии, как на плоскости  а вдоль некоторой кривой, похожей на кубическую параболу.
а вдоль некоторой кривой, похожей на кубическую параболу.



 новую инструментальную переменную
новую инструментальную переменную  и, тем самым, построим регрессионную модель вида:
и, тем самым, построим регрессионную модель вида: .
.
 .
. вектора измеримых j -факторов,
вектора измеримых j -факторов,  - вектор общих (латентных) факторов
- вектор общих (латентных) факторов 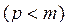 ,
, 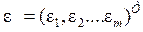 - вектор частных (специфических) факторов, присущих именно измеримым факторам.
- вектор частных (специфических) факторов, присущих именно измеримым факторам.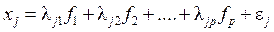 .
.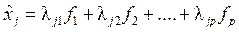 и характерной специфической части
и характерной специфической части 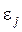 .
. 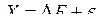 ,
,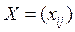 матрица измерений
матрица измерений  ,
, 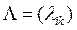 - матрица факторных нагрузок
- матрица факторных нагрузок  ,
, 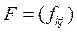 - матрица значений общих факторов
- матрица значений общих факторов 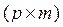 ,
, 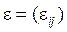 -матрица специфичности
-матрица специфичности 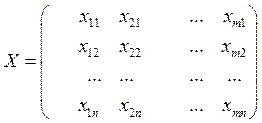 ,
, 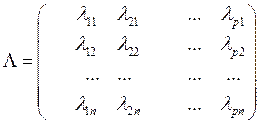 ,
, 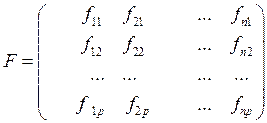 ,
, 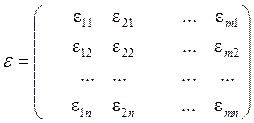 .
.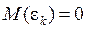 несмещённость специфических факторов,
несмещённость специфических факторов,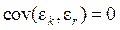 некоррелируемость специфических факторов,
некоррелируемость специфических факторов, гомоскедастичность специфических факторов,
гомоскедастичность специфических факторов, нормальность специфических факторов.
нормальность специфических факторов.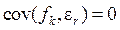 некоррелируемость общих и специфических факторов между собой.
некоррелируемость общих и специфических факторов между собой. и упорядоченность их факторной дисперсии
и упорядоченность их факторной дисперсии 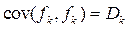 по убыванию
по убыванию 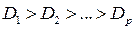 . Последнее требование позволяет назвать первый фактор главным, т.к. именно он определяет наибольшую долю факторную изменчивость
. Последнее требование позволяет назвать первый фактор главным, т.к. именно он определяет наибольшую долю факторную изменчивость  . Чем больше первые факторные дисперсии и чем меньше последние, тем выше качество факторной модели. Количество общих факторов p должно быть не большим, по крайней мере
. Чем больше первые факторные дисперсии и чем меньше последние, тем выше качество факторной модели. Количество общих факторов p должно быть не большим, по крайней мере  , это позволит провести уменьшение размерности задачи анализа измеренных величин. Такое сжатие информации об измеренных объектах позволит эффективно и наглядно решать задачи о классификации наблюдаемых объектов в задачах кластерного анализа.
, это позволит провести уменьшение размерности задачи анализа измеренных величин. Такое сжатие информации об измеренных объектах позволит эффективно и наглядно решать задачи о классификации наблюдаемых объектов в задачах кластерного анализа. в центральной нормированной системе координат новую систему координат
в центральной нормированной системе координат новую систему координат  повёрнутую на угол
повёрнутую на угол  и в каждой из них прямоугольник, охватывающий корреляционное поле. На рисунке 6.1 видно, что размеры этих прямоугольников различны, но ведь они соответствуют дисперсиям наблюдаемых величин, причём как видим из рисунка
и в каждой из них прямоугольник, охватывающий корреляционное поле. На рисунке 6.1 видно, что размеры этих прямоугольников различны, но ведь они соответствуют дисперсиям наблюдаемых величин, причём как видим из рисунка 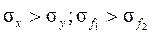 ,
, 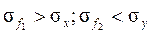 .
.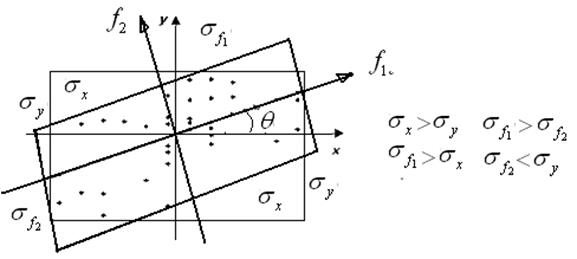
 первая дисперсия увеличилась, а вторая уменьшилась. Это подсказывает, что новые факторы можно вводить как новую систему координат, повёрнутую относительно исходной системы, где произведены измерения. Преобразование поворота прямоугольной системы координат известно:
первая дисперсия увеличилась, а вторая уменьшилась. Это подсказывает, что новые факторы можно вводить как новую систему координат, повёрнутую относительно исходной системы, где произведены измерения. Преобразование поворота прямоугольной системы координат известно: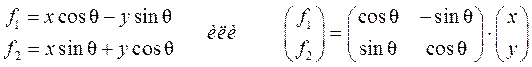
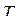 можно выбрать из различных соображений, например, в методе центройд [3], ось главного фактора
можно выбрать из различных соображений, например, в методе центройд [3], ось главного фактора  направляется на наиболее удалённую точку корреляционного поля, а ось фактора
направляется на наиболее удалённую точку корреляционного поля, а ось фактора 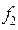 должна быть перпендикулярной к оси
должна быть перпендикулярной к оси 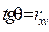 , так как регрессия имеет вид
, так как регрессия имеет вид 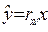 .
.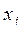 в новые координаты
в новые координаты 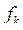 , которые и будут общими факторами, причём размерность пространства при повороте не меняется
, которые и будут общими факторами, причём размерность пространства при повороте не меняется 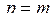 . Запишем преобразование через матрицу поворота
. Запишем преобразование через матрицу поворота 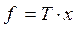 ;
;  , где
, где 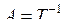 обратная матрица поворота.
обратная матрица поворота. для обеспечения ортогональности новой системы координат;
для обеспечения ортогональности новой системы координат;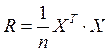 симметричная корреляционная матрица в нормированной исходной системе измерений
симметричная корреляционная матрица в нормированной исходной системе измерений 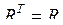 , а
, а 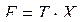 преобразованная вращением матрица измерений в новых факторных переменных, она несимметрична
преобразованная вращением матрица измерений в новых факторных переменных, она несимметрична 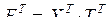 . Тогда корреляционная матрица в новых координатах будет следущей:
. Тогда корреляционная матрица в новых координатах будет следущей: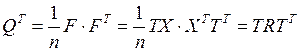 .
.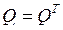 была бы диагональной, что обеспечит независимость новых факторных переменных. Это требование будет выполнено, если матрица поворота построена из собственных векторов корреляционной матрицы
была бы диагональной, что обеспечит независимость новых факторных переменных. Это требование будет выполнено, если матрица поворота построена из собственных векторов корреляционной матрицы  . Собственные вектора
. Собственные вектора 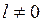 находятся из условия,
находятся из условия,  или
или 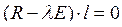 которое разрешимо при значении величин
которое разрешимо при значении величин  , удовлетворяющих характеристическому уравнению
, удовлетворяющих характеристическому уравнению  . Это алгебраическое уравнение порядка
. Это алгебраическое уравнение порядка  для симметричной положительно определенной матрицы
для симметричной положительно определенной матрицы  имеет
имеет 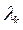 , называемых собственными числами корреляционной матрицы. Упорядочив их по убыванию значения и найдя каждому из них соответствующий собственный вектор
, называемых собственными числами корреляционной матрицы. Упорядочив их по убыванию значения и найдя каждому из них соответствующий собственный вектор  единичной длины, можем построить следующую матрицу поворота
единичной длины, можем построить следующую матрицу поворота 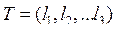 . Корреляционная матрица в факторных переменных будет диагональной
. Корреляционная матрица в факторных переменных будет диагональной 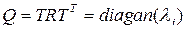 с диагональными элементами
с диагональными элементами  . Такое преобразование матрицы оставляет инвариантным её след
. Такое преобразование матрицы оставляет инвариантным её след  , а так как
, а так как 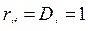 и
и 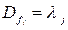 , то выполнено следующее
, то выполнено следующее  .
.


