
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальная случайная величина
Случайная величина имеет нормальный закон распределения (закон Гаусса), если она определена в области
где Нормальный закон распределения Плотность вероятности При уменьшении только параметра
Рис. 1.8. Функция плотности распределения нормальной величины Функция распределения
Рис. 1.9. Функция распределения нормальной величины
Вероятность того, что изучаемая случайная величина (распределённая нормально) примет значение в пределах от
В частном случае, когда интервал симметричен относительно точки
Рассмотрим вероятность того, что изучаемая случайная величина (распределённая нормально) примет значение в пределах от
т.е. вероятность значений изучаемой случайной величины именно на интервале
Пример. Наблюдение за скоростью автомашин на определённом участке дороги показало, что скорость есть нормальная случайная величина с математическим ожиданием 60 км/ч и среднеквадратическим отклонением 10 км/ч. Определить вероятность того, что: - скорость на этом участке не превышает 80 км/ч, - скорость не отклоняется от математического ожидания более чем на 20%. Поскольку скорость есть нормальная величина с параметрами
Вычислим скорость, которую автомашины на этом участке не превышают с вероятностью 0,99. Из уравнения
Системы случайных величин
Если рассматривается система случайных величин
- они могут быть независимыми, когда распределение каждой из них не зависит от того, какие значения примут другие величины. Например, - они могут быть зависимы функционально, когда между значениями величин имеется функциональная связь вида Y =φ(X). Так, площадь выражается через измерения случайных размеров. Связь между распределениями величин устанавливается достаточно просто при взаимно однозначной функциональной связи [4]:
где
- случайные величины могут быть зависимыми статистически, когда распределение каждой случайной величины зависит от того, какие значения принимают другие величины. Например, Такая зависимость полностью может быть описана условными распределениями величин. Так, для пары величин
причем, оказывается, что
Часто рассматриваются условные математические ожидания величин
такая зависимость средних значений (математических ожиданий) от значения других переменных называется регрессией. Функция регрессии
Рис. 1.10. Функция регрессии для зависимых величин
В случае независимости величин условные распределения совпадают и В случае статистической зависимости введём понятие ковариационного момента (ковариации):
который показывает степень статистической зависимости величин
Введем также безразмерную величину коэффициента корреляции
обладающего следующими свойствами: - его значение по модулю не превышает единицы - для независимых величин - для линейно зависимых величин Это позволяет использовать коэффициент корреляции в качестве меры статистической зависимости случайных величин. Говорят, что величины коррелируют между собой, если коэффициент корреляции не равен нулю.
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.8.216 (0.013 с.) |
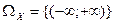 , а её плотность распределения вероятностей имеет вид:
, а её плотность распределения вероятностей имеет вид: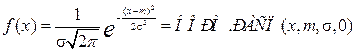
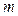 и
и 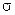 - параметры распределения (
- параметры распределения (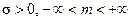 ).
).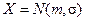 наиболее часто встречается на практике. Главная его особенность – он является предельным законом, которым приближаются другие, более сложные законы распределения [7].
наиболее часто встречается на практике. Главная его особенность – он является предельным законом, которым приближаются другие, более сложные законы распределения [7].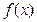 похожа на «колокол» (рис. 1.8).
похожа на «колокол» (рис. 1.8). , график перемещается вдоль оси абсцисс.
, график перемещается вдоль оси абсцисс.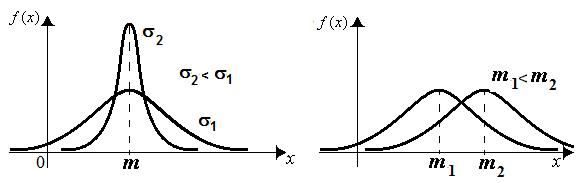
 нормальной величины имеет вид:
нормальной величины имеет вид:
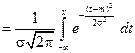
 ,
,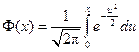 - функция Лапласа. График функции распределения
- функция Лапласа. График функции распределения  изображен на рис. 1.9.
изображен на рис. 1.9.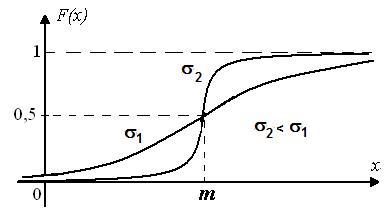
 до
до 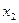 вычисляется по обычной формуле:
вычисляется по обычной формуле:
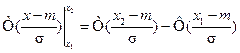 .
. 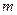 , эта формула выглядит так:
, эта формула выглядит так: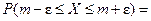

 .
.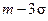 до
до 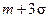 :
: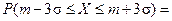
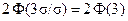
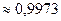 ,
,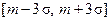 велика. Это утверждение составляет правило «трёх сигм». Числовые характеристики нормальной случайной величины будут:
велика. Это утверждение составляет правило «трёх сигм». Числовые характеристики нормальной случайной величины будут: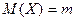 ,
, 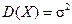 .
.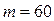 и
и 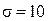 , то по основным формулам находим:
, то по основным формулам находим: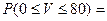
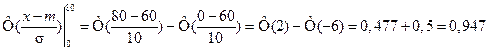 ,
,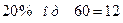

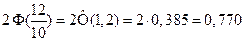 .
.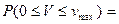
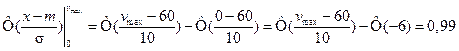 ,
,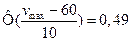
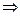

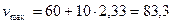 .
. , то между ними могут быть следующие взаимные соотношения:
, то между ними могут быть следующие взаимные соотношения: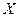 -температура воды на входе системы отопления жилого многоквартирного дома, а
-температура воды на входе системы отопления жилого многоквартирного дома, а 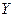 - количество жильцов, проживающих в доме, эти величины независимы;
- количество жильцов, проживающих в доме, эти величины независимы;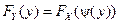 ,
, 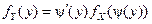 ,
,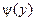 обратная для φ (x) функция. Например, для равномерной
обратная для φ (x) функция. Например, для равномерной 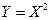 :
: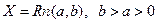 ,
,  ,
, 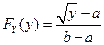 ,
, 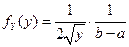 ;
;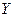 - количество жильцов, обратившихся с жалобой в ДУК на холод в квартирах, эти величины зависимы статистически.
- количество жильцов, обратившихся с жалобой в ДУК на холод в квартирах, эти величины зависимы статистически.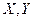 условное распределение задаётся функцией двух переменных
условное распределение задаётся функцией двух переменных  или
или 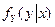 , представляющих собой распределения одной величины при заданном значении другой величины. Распределения самих величин связаны с условными распределениями следующим образом:
, представляющих собой распределения одной величины при заданном значении другой величины. Распределения самих величин связаны с условными распределениями следующим образом: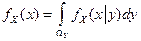 ,
, 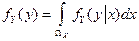 ,
, , а
, а 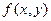 называется функцией совместного распределения и она связана с вероятностью значений величин через функцию совместного распределения
называется функцией совместного распределения и она связана с вероятностью значений величин через функцию совместного распределения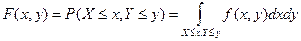 .
.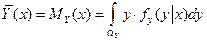 ,
, 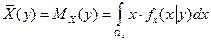 ,
,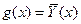 и условные распределения иллюстрируются на рисунке 1.10.
и условные распределения иллюстрируются на рисунке 1.10.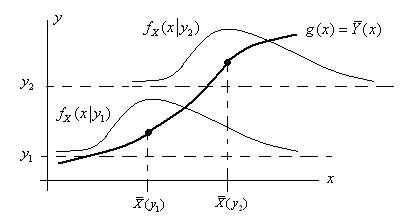

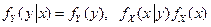 , а
, а 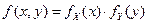 ,
,  .
. ,
,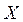 и
и 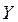 , поскольку при независимости переменных он равен нулю, а для статистически зависимых величин справедливы следующие формулы:
, поскольку при независимости переменных он равен нулю, а для статистически зависимых величин справедливы следующие формулы: ,
,  .
.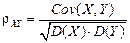 ,
,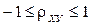 .
.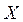 и
и 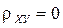 ,
,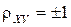 .
.


