
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайных величинСтр 1 из 7Следующая ⇒
Закон распределения случайной величины, заданный в той или иной форме, полностью определяет случайную величину как некоторую модель наблюдаемого в опыте явления. Однако часто в практической деятельности знание закона бывает невозможным, а то и избыточным, достаточно знать лишь некоторые общие (интегральные) характеристики случайной величины. Пусть случайная величина Математическое ожидание:
Дисперсия:
Среднеквадратическое отклонение:
Математическое ожидание
Среднеквадратическое отклонение
Рис. 1.6. Геометрическая иллюстрация понятий математического ожидания
Пример. Рассмотрим случайную величину
Рис. 1.7. Функция распределения
Математическое ожидание постоянной величины равно этой постоянной величине, а её дисперсия равна нулю:
Умножение случайной величины на постоянный множитель приводит к следующему изменению её характеристик:
Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий этих величин:
Из вышеприведённых свойств можно заметить, что при преобразовании случайной величины
Такое преобразование случайной величины называется центрированием и нормированием, а характеристики получаемой величины называются стандартными. Для независимых случайных величин
Величины называются независимыми, если распределение любой из них не зависит от того, какие значения принимает другая величина. В противном случае величины являются статистически зависимыми.
|
|||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 76; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.231 (0.009 с.) |
 , дискретная или непрерывная, задается законом распределения, тогда основными характеристиками случайной величины являются:
, дискретная или непрерывная, задается законом распределения, тогда основными характеристиками случайной величины являются:
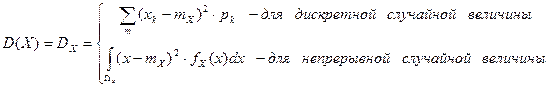
 .
. 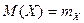 характеризует центр распределения или средневзвешенное ожидаемое значение величины, а геометрически оно изображается как координата центра тяжести фигуры, образованной осью
характеризует центр распределения или средневзвешенное ожидаемое значение величины, а геометрически оно изображается как координата центра тяжести фигуры, образованной осью  и линией функции
и линией функции  или
или 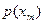 . Дисперсия
. Дисперсия  характеризует средний ожидаемый разброс (широту, изменчивость, вариативность) значений величины возле
характеризует средний ожидаемый разброс (широту, изменчивость, вариативность) значений величины возле 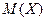 , поскольку совпадает с математическим ожиданием квадрата отклонения случайной величины от его математического ожидания.
, поскольку совпадает с математическим ожиданием квадрата отклонения случайной величины от его математического ожидания.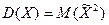 , где
, где 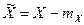 .
.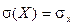 имеет тот же смысл, что и дисперсия, но в отличие от неё имеет размерность, совпадающую с размерностью самой случайной величины, что более удобно и позволяет изобразить его как и математическое ожидание на рис. 1.6. Между дисперсией и математическим ожиданием имеется простая связь
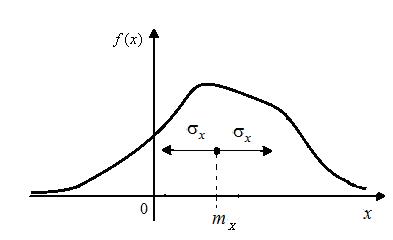
имеет тот же смысл, что и дисперсия, но в отличие от неё имеет размерность, совпадающую с размерностью самой случайной величины, что более удобно и позволяет изобразить его как и математическое ожидание на рис. 1.6. Между дисперсией и математическим ожиданием имеется простая связь  .
.
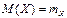 и дисперсии
и дисперсии 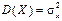 случайной величины
случайной величины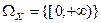 со следующим законом распределения
со следующим законом распределения  ,
, 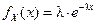 , где параметр
, где параметр 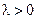 . Такая случайная непрерывная величина называется показательной ( рис. 1.7).
. Такая случайная непрерывная величина называется показательной ( рис. 1.7).
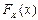 и плотность распределения
и плотность распределения  показательной случайной величины
показательной случайной величины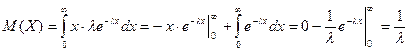


 const
const  ,
,  .
.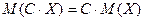 ,
, 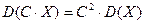 , где
, где  const.
const. .
.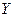
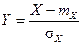
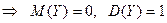 .
.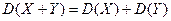 ,
,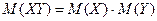 .
.


