
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения динамического пограничного слояСодержание книги
Поиск на нашем сайте
Дифференциальные уравнения динамического пограничного слояполучаются на основе дифференциальных уравнений движения и неразрывности. Рассмотрим вывод уравнений для двумерного стационарного течения вдоль оси x. Влиянием массовых сил пренебрегаем. Выпишем исходные уравнения Навье-Стокса в безразмерном виде, введя характерные масштабные множители:
Проведём оценку порядка величин входящих в уравнения (1). Сущность оценки порядка величины можно понять на следующем примере. Если какая-то величина z меняется в диапазоне от 0 до z0, то мы говорим, что это величина порядка z0, а безразмерная величина Оценка для всех членов уравнений (1) выглядит следующим образом:
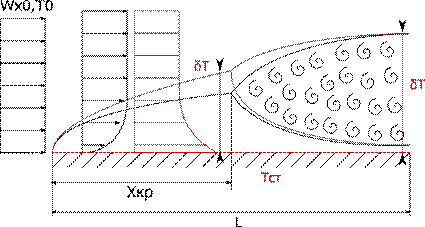
В пределе при или в размерном виде: Как следует из вывода, уравнения пограничного слоя строго справедливы только при числе Рейнольдса Re→∞, при этом по толщине пограничного слоя давление не изменяется, а поперечная скорость потока wy пропорциональна толщине пограничного слоя и может быть выражена следующим образом: Из оценки величины числа Рейнольдса можно получить выражение для оценки толщины динамического пограничного слоя: Существует также понятие теплового пограничного слоя – это область течения вблизи обтекаемой поверхности, в которой температура потока изменяется от температуры стенки до температуры внешнего течения.
Дифференциальное уравнения теплового пограничного слоя можно получить тем же методом оценки порядка величин и для рассматриваемого случая оно выглядит следующим образом: при этом уравнение теплового пограничного слоя существует при Из оценки величины числа Пекле можно получить выражение для оценки толщины теплового пограничного слоя: При течении жидкости без градиента давления и Pr=1 безразмерная форма уравнений движения (4) и энергии (7) полностью совпадают, а значит, совпадают и их решения. С точки зрения теории пограничного слоя это означает, что тепловой и динамический пограничные слои будут иметь одинаковую толщину по всей дине пластины. При Pr<1 тепловой пограничный слой будет больше динамического Полученные дифференциальные уравнения пограничного слоя проще соответствующих полных дифференциальных уравнений Навье-Стокса. Тем не менее, аналитические решения данной системы уравнений существуют только для нескольких частных случаев, таких как течение над проницаемой пластиной с отсосом газа из пограничного слоя, течение в гладкой трубе и ряд других. Разработаны надёжные и экономичные методы численного интегрирования данной системы уравнений, позволяющие получить решения для широкого круга задач и граничных условий. В частности решение уравнений (5) для задачи определения сопротивления плоской непроницаемой пластины набегающему потоку воздуха под нулевым углом атаки впервые было получено Блазиусом: Процесс численного интегрирования зачастую становится громоздким и трудоемким. В этой связи большое значение приобрели приближенные методы решения указанных уравнений, основанные на применении так называемых интегральных соотношений импульсов и энергии. Интегральные соотношения получаются в результате интегрирования дифференциальных уравнений движения и энергии по толщине пограничного слоя. Интегральные уравнения пограничного слоя являются балансовыми для рассматриваемого сечения пограничного слоя и сами по себе точные, по крайней мере, в рамках теории пограничного слоя. Приближенный характер решения этих уравнений обусловлен способом их замыкания.
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.89.70 (0.005 с.) |

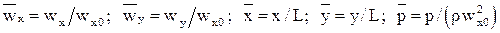 .
.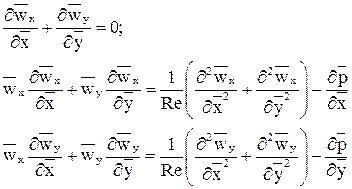 (1)
(1)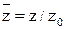 будет иметь порядок 1. В нашем случае в пограничном слое скорость wx меняется от 0 до wx0, значит
будет иметь порядок 1. В нашем случае в пограничном слое скорость wx меняется от 0 до wx0, значит 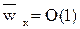 имеет порядок 1, x меняется от 0 до
имеет порядок 1, x меняется от 0 до 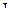 , значит
, значит 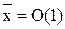 имеет порядок 1. В пределах пограничного слоя y меняется от 0 до d, значит y имеет порядок d, а
имеет порядок 1. В пределах пограничного слоя y меняется от 0 до d, значит y имеет порядок d, а 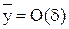 величина порядка
величина порядка 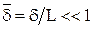 .
.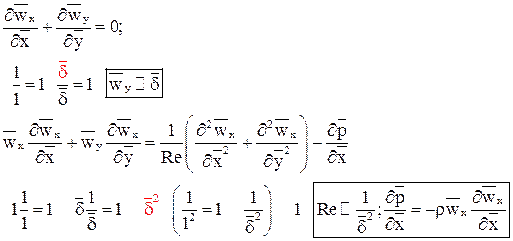 (2)
(2)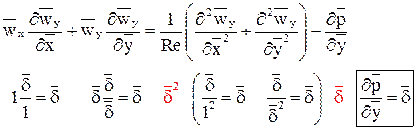 (3)
(3)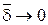 получим систему дифференциальных уравнений динамического пограничного слоя:
получим систему дифференциальных уравнений динамического пограничного слоя: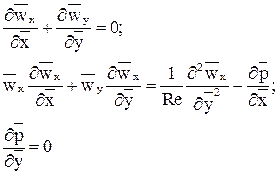 (4)
(4)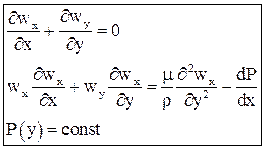 (5)
(5)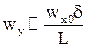
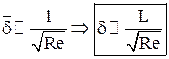 (6)
(6)
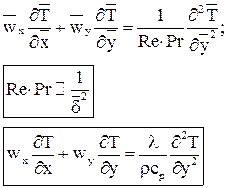 , (7)
, (7)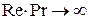 .
.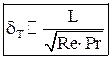 (8)
(8)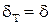 (8)
(8)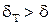 , при Pr>1 наоборот меньше
, при Pr>1 наоборот меньше 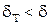 .
.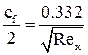 (9)
(9)


