
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения газаСодержание книги
Поиск на нашем сайте
Из представленного феноменологического анализа коэффициента теплоотдачи видно, что наибольшее влияние на его значение оказывает газодинамика течения. Получим дифференциальные уравнения описывающие течение газа. Уравнение неразрывности Уравнение неразрывности представляет собой закон сохранения массы для элементарного объёма жидкости.
Баланс массы в элементарном объёме за время
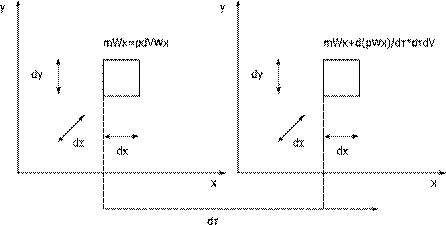
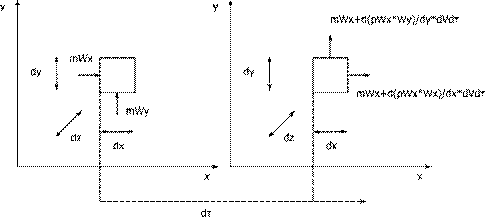
Уравнение движения В классической механике Ньютона движение материального объекта описывается законом сохранения импульса (второй закон Ньютона), который гласит – изменение импульса тела определяется векторной суммой всех сил действующих на тело и времени приложения этих сил. Рассмотрим механическое равновесие элементарного объема жидкости. Как и прежде ограничимся двумерной постановкой. Среди сил, действующих на элементарный объём, рассмотрим только силу давления, силу тяжести, силу трения. Необходимо учесть, что импульс элементарного объёма газообразной или жидкой среды может изменяться и за счёт изменения плотности среды и поступления или отвода жидкости из элементарного объёма. Поскольку уравнение (11) даётся в векторной форме, запишем его члены в проекции на ось координат. Рассмотрим проекцию на ось x (на ось y аналогично). Изменение импульса элементарного объёма за счёт изменения плотности можно записать следующим образом:
Изменение импульса элементарного объёма за счёт подвода массы:
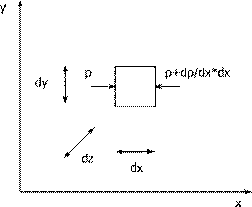
Действие силы давления:
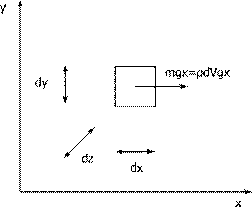
Действие массовой силы (силы тяжести):
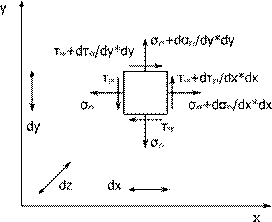
Для анализа действия силы трения необходимо рассмотреть напряжённое состояние элементарного объёма:
Сумма напряжений в проекции на ось x записывается следующим образом:
Объединяя уравнения (12)-(16) получим: или По аналогии выводится уравнение движения в проекции на ось Используя уравнение неразрывности систему уравнений (17), (18) можно привести к виду: Полученная система носит название системы уравнений Навье-Стокса. Как видно система уравнений включает в себя растягивающие и сдвиговые напряжения трения на гранях элементарного объёма. Согласно гипотезе Ньютона эти напряжения можно связать с градиентами скоростей в соответствующих направлениях. где m, [Па×с] - коэффициент динамической вязкости газа. Если принять, что плотность и вязкость газа слабо зависят от температуры и давления в потоке, то уравнения Навье-Стокса можно привести к более простому виду. В совокупности с уравнением теплообмена, полученным на предыдущих лекциях, и уравнением состояния идеального газа уравнения Навье-Стокса являются базой для теоретического анализа теплоотдачи от твёрдых поверхностей, омываемых потоком газа или жидкости:
Здесь n=m/r - коэффициент кинематической вязкости, м2/с. Полученная система дифференциальных уравнений (22) справедлива в любой точке выделенной области течения. Однако решение этой системы уравнений возможно только при известных граничных условиях.
Элементы теории подобия
Система дифференциальных уравнений Навье-Стокса в общем виде не поддаётся аналитическому решению. Разработанные на сегодняшний день численные методы решения с появлением современных компьютеров и суперкомпьютеров дают возможность анализировать достаточно сложные задачи теплообмена, как при ламинарном, так и при турбулентном режиме течения. Однако необходимость применение дорогостоящих вычислительных ресурсов и специализированных программ позволяет применять эти методики только в крупных исследовательских центрах и на ведущих предприятиях авиационной, космической, судостроительной, автомобильной отраслей. До появления современных компьютеров основным методом исследования конвективного теплообмена был натурный эксперимент. Однако следует понимать, что любой эксперимент выполняется в конкретной установке с заданной конфигурацией. Поскольку газодинамика течения и соответственно теплообмен в значительной степени зависят от геометрии обтекаемой поверхности и параметров течения, то определённые в эксперименте коэффициенты теплоотдачи, строго говоря, справедливы только для этой конфигурации и этих параметров течения. Чтобы перенести эти данные на другие конфигурации или другие параметры течения необходимо знать правила перевода. Эти правила устанавливает теория подобия. Теория подобия - это учение о подобных явлениях. В приложении к физическим явлениям теория подобия применяется по двум направлениям: как средство обобщения результатов физического и математического эксперимента и как теоретическая основа для моделирования технических устройств. Таким образом, теория подобия позволяет на основании отдельных опытов или численных расчетов получить обобщенную зависимость и открывает возможность изучения рабочих процессов технических устройств на моделях. Для реализации подобия физических явлений необходима пропорциональность не только геометрических элементов систем, в которых протекают явления, но и других физических характеристик, определяющих эти явления (скоростей, температур, плотностей и т. п.). Введем ряд понятий теории подобия. Одноименными называются величины, имеющие одинаковый физический смысл и одинаковую размерность. Сходственными называются такие точки систем, координаты которых удовлетворяют геометрическому подобию. Сходственные моменты времени наступают по истечении периодов времени, имеющих общее начало отсчета и связанных между собой константой подобия по времени. Подобными называются физические явления, протекающие в геометрически подобных системах, если у них во всех сходственных точках в сходственные моменты времени отношения одноименных величин есть постоянные числа. Эти постоянные числа называются константами подобия. Теплоотдача в двух различных, но подобных системах будет протекать одинаково, если в этих системах одинаковы значения комплекса: Эти комплексы называются числами подобия, и приведённое соотношение носит название числа Нуссельта. Физический смысл числа Нуссельта – отношение теплового потока, передаваемого конвекцией, к тепловому потоку, передаваемому теплопроводностью, при идентичных условиях. Числа подобия принято называть именами крупных учёных внесших вклад в развитие соответствующего направления науки. Таким образом, для характеристики подобия явлений можно использовать константы подобия и числа подобия. Константы подобия сохраняют числовое значение только для двух подобных явлений, но они остаются одинаковыми для всех сходственных точек рассматриваемых систем. Поэтому константами подобия удобно пользоваться при моделировании технических устройств, когда необходимо получить подобие только между двумя явлениями. Числа подобия сохраняют свое значение в сходственных точках всех подобных между собой систем, сколько бы их ни было, но в различных точках одной и той же системы числа имеют разные значения. Числами подобия удобно пользоваться при обработке опытных данных или численных расчетов, когда на основании изучения единичных явлений необходимо получить обобщенную зависимость, пригодную для всех подобных между собой явлений. Формулы связи между числами подобия называются уравнениями подобия. Число Рейнольдса отражает интенсивность вынужденного движения газа или жидкости (отношение сил инерции и вязкостного трения). Число Грасгофа определяет интенсивность свободно-конвективного движения. Вводя понятие коэффициента объёмного расширения Число Пекле отражает интенсивность конвективного переноса тепла по сравнению с переносом тепла теплопроводностью. Не трудно заметить, что число Пекле можно представить в виде: Число Прандтля отражает влияние теплофизических свойств газа или жидкости на теплообмен. Число Фурье характеризует динамику нестационарной теплопроводности (безразмерное время). Существует ещё ряд комплексов, которые часто используются в теории теплообмена. Число Стентона – аналог числа Нуссельта, связывающий интенсивность теплоотдачи с конвективным переносом тепла: Коэффициент трения – отражает действие вязких сил при заданном динамическом напоре газового потока: Таким образом, чтобы в результате опытного исследования процесса трения и теплоотдачи получить формулу, пригодную для оценки не только исследованных явлений, но и всех явлений, подобных исследованным, результаты опытов необходимо представить в виде зависимостей. В стационарных условиях зависимость между трением и теплоотдачей будут выглядеть, следующим образом: В задачах с определяющим действием вынужденной конвекции: В задачах свободной конвекции: Для удобства обработки опытных данных уравнения подобия принято представлять в виде степенной функции: где c, k, m и n - опытные коэффициенты. Выражая напряжение трения через коэффициент трения, а коэффициент теплоотдачи через число Нуссельта получим: При значениях числа Прандтля в диапазоне от 0,6 до 1 (в том числе для воздуха) связь трения и теплообмена может быть представлена в следующем виде: Зависимость между теплоотдачей и трением глубоко вскрывает физический смысл явления теплоотдачи и позволяет использовать величины коэффициентов сопротивления, определенные опытным или теоретическим путем, для оценки коэффициентов теплоотдачи. Экспериментальное определение коэффициентов сопротивления обычно значительно проще, чем коэффициентов теплоотдачи. Поэтому для систем, явление теплоотдачи в которых экспериментальным путем не изучалось, полученные выше соотношения могут служить средством получения расчетных формул для коэффициентов теплоотдачи.
§7. вынужденное движение жидкости (газа). Понятие пограничного слоя
7.1. Краткая история возникновения теории пограничного слоя Дифференциальные уравнения движения вязкой жидкости и уравнение энергии были получены в середине XIX века. До начала XX в. теоретическое решение многих практически важных задач теплообмена и гидродинамики было затруднительно. Это объясняется тем, что аналитическое решение полных уравнений движения невозможно, а численное решение требует применения мощных компьютеров. В XIX веке были решены лишь некоторые частные задачи, в которых полагались равными нулю конвективные производные (инерционные силы) в уравнениях Навье-Стокса. Одной из таких задач является задача определения гидравлического сопротивления при развитом ламинарном течении жидкости в трубе. Вместе с тем в XIX веке были достигнуты большие успехи в изучении движения идеальной (лишенной свойства вязкости) жидкости. С помощью уравнений Эйлера можно рассчитать поле скорости в окрестности обтекаемого тела и определить силы давления на поверхность тела. Однако теория движения идеальной жидкости не объясняла причину возникновения вихрей в кормовой части плохо обтекаемых тел. В случае поперечного обтекания цилиндра она приводила к парадоксу Даламбера: ввиду симметричного распределения давления по окружности цилиндра сила сопротивления равна нулю.
В 1904 году немецкий ученый Л. Прандтль опубликовал работу «О движении жидкости при очень малом трении», в которой обратил внимание на то, что при обтекании твердого тела влияние сил вязкости может быть существенным только в области тонкого пограничного слоя, а за его пределами им можно пренебречь. Другими словами, весь поток жидкости он разбил на две части: внешний поток и пограничный слой. Для внешнего потока справедлива теория движения идеальной жидкости (т.е. справедливы уравнения Эйлера). Для пограничного слоя справедливы уравнения Навье-Стокса, причем посредством такого допущения, как малая толщина пограничного слоя Таким образом, были заложены основы теории пограничного слоя, которая сыграла большую роль в изучении процессов тепломассообмена. Достижения в развитии авиации и ракетно-космической техники неразрывно связаны с успехами в решении проблем теории пограничного слоя. При обтекании твердого тела потоком жидкости или газа вблизи поверхности благодаря силам вязкости происходит резкое уменьшение скорости, и на поверхности тела она становится равной нулю. Слой жидкости, в котором скорость движения изменяется наиболее существенно, называется динамическим пограничным слоем.
Теоретически изменение скорости может наблюдаться на большом расстоянии от поверхности, но вдали от тела скорость изменяется несущественно. Толщиной динамического пограничного слоя Толщина динамического пограничного слоя зависит от вязкости и скорости потока, а также от положения рассматриваемого сечения на поверхности: чем меньше вязкость жидкости и больше ее скорость, чем меньше расстояние рассматриваемого сечения от начала формирования пограничного слоя, тем тоньше пограничный слой.
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.168.40 (0.007 с.) |

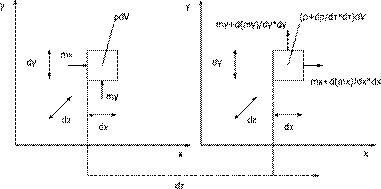
 равен:
равен: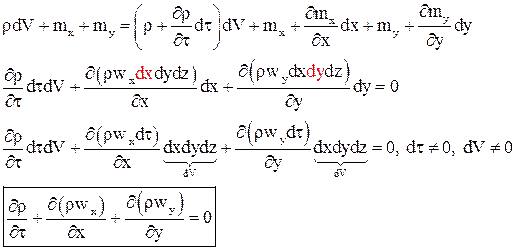
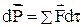 (11)
(11)
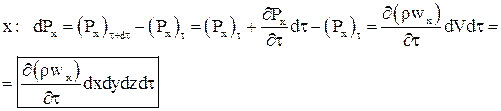 (12)
(12)
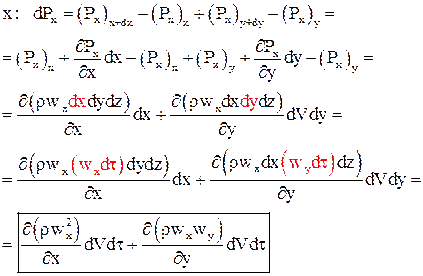 (13)
(13)
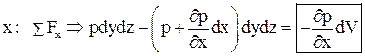 (14)
(14)
 (15)
(15)
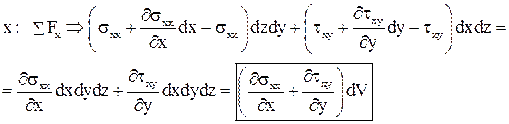 (16)
(16)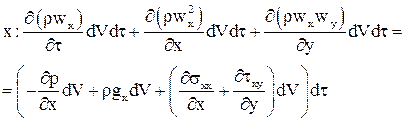
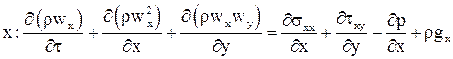 (17)
(17)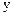 :
: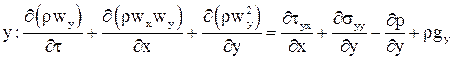 (18)
(18)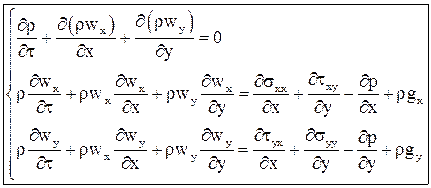 (19)
(19)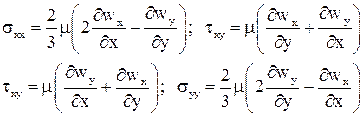 , (20)
, (20)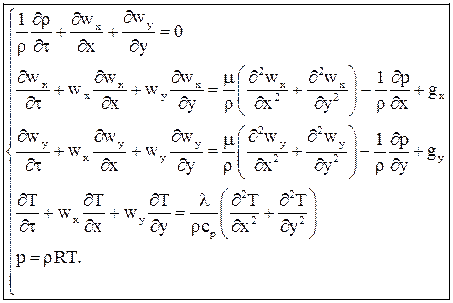 (22)
(22)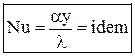 (1)
(1)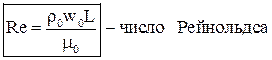 (2)
(2)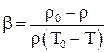 комплекс можно преобразовать к виду:
комплекс можно преобразовать к виду: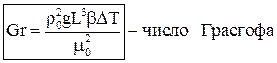 (3)
(3)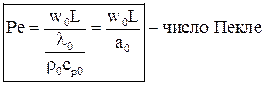 (4)
(4)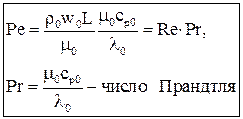 (5)
(5)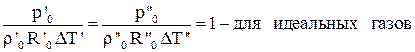 (6)
(6)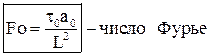 (7)
(7)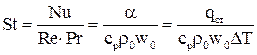 (8)
(8)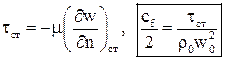 (9)
(9)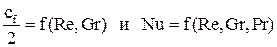 (10)
(10)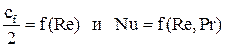 (11)
(11)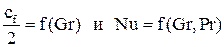 (12)
(12)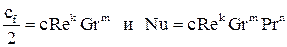 ,
, 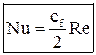 (4)
(4)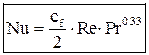 (5)
(5)
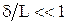 , эти уравнения удалось существенно упростить.
, эти уравнения удалось существенно упростить.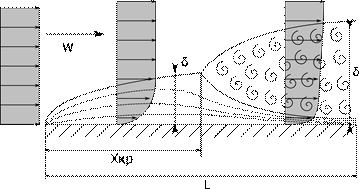
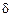 условились считать расстояние от твердой стенки до поверхности, где скорость составляет 99% от скорости невозмущенного потока.
условились считать расстояние от твердой стенки до поверхности, где скорость составляет 99% от скорости невозмущенного потока.


