
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические схемы моделирования систем
Наибольшие затруднения и серьезные ошибки при моделировании возникают при переходе от содержательного к формальному описанию объектов исследования, что объясняется участием в этом творческом процессе коллективов разных специальностей: специалистов в области систем, которым требуется моделировать (заказчиков), и специалистов в области машинного моделирования (исполнителей). Эффективным средством для нахождения взаимопонимания между этими группами специалистов является язык математических схем, позволяющий во главу угла поставить вопрос об адекватности перехода от содержательного описания системы к её математической схеме, а лишь затем решать вопрос о конкретном методе получения результатов с использованием ЭВМ: аналитическом или имитационном, возможно и комбинирование, т.е. аналитико-имитационном. Основные подходы к построению математических моделей систем Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования систем S и позволяет сформулировать требования к разрабатываемой математической модели М, причем уровень абстрагирования зависит от круга тех вопросов, на которые исследователь системы хочет получить ответ с помощью модели, и в какой-то степени определяет выбор математической схемы. Математические схемы Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т.е. имеет место цепочка «описательная модель - математическая схема - математическая [аналитическая или (и) имитационная] модель». Каждая конкретная система S характеризуется набором свойств, под которыми понимаются величины, отражающие поведение моделируемого объекта (реальной системы) и учитывающие условия ее функционирования во взаимодействии с внешней средой (системой) Е. При построении математической модели системы необходимо решить вопрос об ее полноте. Полнота модели регулируется в основном выбором границы «система S - среда Е». Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы, отбросив второстепенные. Причем отнесение свойств системы к основным или второстепенным существенно зависит от цели моделирования системы (например, анализ вероятностно-временных характеристик процесса функционирования системы, синтез структуры системы и т.д.).
Формальная модель объекта Модель объекта моделирования, т.е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества: совокупность входных воздействий на систему
совокупность воздействий внешней среды
совокупность внутренних (собственных) параметров системы
совокупность выходных характеристик системы
При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае Процесс функционирования системы S описывается во времени оператором
Совокупность зависимостей выходных характеристик системы от времени Весьма важными для описания и исследования системы S является понятие алгоритма функционирования
Соотношения Для статических моделей математическая модель
Соотношения
где …, Если рассматривать процесс функционирования системы S как последовательную смену состояний Состояния системы S в момент времени
моделирование математический познание Первое уравнение по начальному состоянию
В общем случае время модели системы S может рассматриваться на интервале моделирования (0, Т) как непрерывное, так и дискретное, т.е. квантованное на отрезки длинной Таким образом, под математической моделью объекта (реальной системы) понимают конечное подмножество переменных Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т.е. если можно считать, что в этом случае стохастические воздействия внешней среды
Очевидно, что детерминированная модель является частным случаем стохастической модели. Типовые схемы Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри и т.д. Не обладая такой степенью общности, как рассмотренные модели, типовые математические схемы имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения. В качестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегро-дифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени, - конечные автоматы и конечно-разностные схемы. В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления системы с непрерывным временем - системы массового обслуживания и т.д. Перечисленные типовые математические схемы, естественно, не могут претендовать на возможность описания на их базе всех процессов, происходящих в больших информационно-управляющих системах. Для таких систем в ряде случаев более перспективным является применение агрегативных моделей. Агрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей. Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный (например, дифференциальные уравнения); дискретно-детерминированный (конечные автоматы); дискретно-стохастический (вероятностные автоматы); непрерывно-стохастический (системы массового обслуживания); обобщенный, или универсальный (агрегативные системы).
Непрерывно-детерминированные модели Рассмотрим особенности непрерывно-детерминированного подхода на примере использования в качестве математических модели дифференциальных уравнений. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные - функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной неизвестной переменной уравнения называются обыкновенными дифференциальными уравнениями.
Основные соотношения Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем
Где Так как математические схемы такого вида отражают динамику изучаемой системы, т.е. её поведение во времени, то они называются D-схемами (англ. dynamic). В простейшем случае обыкновенное дифференциальное уравнение имеет вид
Наиболее Важно для системотехники приложение D-схем в качестве математического аппарата в теории автоматического управления. Для иллюстрации особенностей построения и применения D-схем рассмотрим простейший пример формализации процесса функционирования двух элементарных систем различной физической природы: механической
Рис. 1.0. Элементарные системы
Процесс малых колебаний маятника описывается обыкновенным дифференциальным уровнем
где Из этого уравнения свободного колебания маятника можно найти оценки интересующих характеристик. Например, период колебания маятника
Аналогично, процессы в электрическом колебательном контуре описываются обыкновенным дифференциальным уравнением
где Из этого уравнения можно получить различные оценки характеристик процесса в колебательном контуре. Например, период характеристических колебаний
Очевидно, что, введя обозначения
где Таким образом, поведение этих двух объектов может быть исследовано на основе общей математической модели Если изучаемая система
Сточки зрения общей схемы математической модели Дискретно-детерминированные модели Особенности дискретно-детерминированного подхода на этапе формализации процесса функционирования систем рассмотрим на примере использования в качестве математического аппарата теории автоматов. Теория автоматов - это раздел теоретической кибернетики, в котором изучаются математические модели - автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции и целесообразной степени общности. Основные соотношения Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами. Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: конечным множеством Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент Таким образом, работа конечного автомата происходит по следующей схеме: в каждом
для
Автомат второго рода, для которого
т.е. функция выходов не зависит от входной переменной Таким образом, уравнение - По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом, согласно -
Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов х и у, состоят из двух букв. По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F -автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» и в соответствии с уравнениями
|
|||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.34.146 (0.073 с.) |




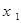 ,
,  ,
,  ,
,  являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие. При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид
являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие. При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид  а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид 
 , который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида
, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида

 для всех видов
для всех видов  называется выходной траекторией
называется выходной траекторией  . Зависимость называется законом функционирования системы S и обозначается
. Зависимость называется законом функционирования системы S и обозначается  . В общем случае закон функционирования системы
. В общем случае закон функционирования системы  , под которым понимается метод получения выходных характеристик с учетом выходных воздействий
, под которым понимается метод получения выходных характеристик с учетом выходных воздействий  воздействий внешней среды
воздействий внешней среды  и собственных параметров системы
и собственных параметров системы 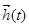 . Очевидно, что один и тот же закон функционирования
. Очевидно, что один и тот же закон функционирования  системы S может быть реализован различными способами, т.е. с помощью множества различных алгоритмов функционирования
системы S может быть реализован различными способами, т.е. с помощью множества различных алгоритмов функционирования  .
. являются математическим описанием поведения объекта (системы) моделирование во времени t, т.е. отражают его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями (системами).
являются математическим описанием поведения объекта (системы) моделирование во времени t, т.е. отражают его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями (системами). представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, H}, что в векторной форме может быть записано как
представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, H}, что в векторной форме может быть записано как
 и
и  могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т.д. Такие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состояниями. Состояние системы S характеризуется векторами
могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т.д. Такие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состояниями. Состояние системы S характеризуется векторами и
и  ,
, в момент
в момент 
 в момент
в момент 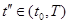 и т.д.,
и т.д., 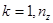
 то они могут быть интерпретированы как координаты точки в k-мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний
то они могут быть интерпретированы как координаты точки в k-мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний 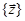 называется пространством состояний объекта моделирования Z, причем
называется пространством состояний объекта моделирования Z, причем 
 полностью определяется начальными условиями
полностью определяется начальными условиями  [где
[где  ], входными воздействиями
], входными воздействиями  внутренними параметрами
внутренними параметрами  и воздействиями внешней среды
и воздействиями внешней среды 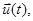 которые имели место за промежуток времени
которые имели место за промежуток времени  с помощью двух векторных уравнений
с помощью двух векторных уравнений

 и экзогенным переменным
и экзогенным переменным  определяет вектор-функцию
определяет вектор-функцию  а второе по полученному значению состояний
а второе по полученному значению состояний  - эндогенные переменные на выходе системы
- эндогенные переменные на выходе системы  Таким образом, цепочка уравнений объекта «вход - состояния - выход» позволяет определить характеристики системы
Таким образом, цепочка уравнений объекта «вход - состояния - выход» позволяет определить характеристики системы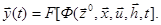
 временных единиц каждый, когда
временных единиц каждый, когда  где
где  - число интервалов дискретизации.
- число интервалов дискретизации. вместе с математическими связями между ними и характеристиками
вместе с математическими связями между ними и характеристиками  и стохастические внутренние параметры
и стохастические внутренние параметры  отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями
отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями
 в общем виде будет
в общем виде будет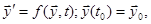
 и
и  - n-мерные векторы;
- n-мерные векторы;  - вектор-функция, которая определена на некотором
- вектор-функция, которая определена на некотором  - мерном
- мерном  множество и является непрерывной.
множество и является непрерывной.
 (маятника, рис. 1, а) и электрической
(маятника, рис. 1, а) и электрической  (колебательный контур, рис. 1.0, б).
(колебательный контур, рис. 1.0, б).

 - масса и длинна подвеса маятника; g - ускорение свободного падения;
- масса и длинна подвеса маятника; g - ускорение свободного падения; 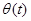 - угол отклонения маятника в момент времени
- угол отклонения маятника в момент времени 
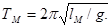

 - индуктивность и емкость конденсатора;
- индуктивность и емкость конденсатора;  - заряд конденсатора в момент времени
- заряд конденсатора в момент времени 

 получим обыкновенное дифференциальное уравнение второго порядка, описывающее поведение этой замкнутой системы:
получим обыкновенное дифференциальное уравнение второго порядка, описывающее поведение этой замкнутой системы:
 параметры системы;
параметры системы;  состояние системы в момент времени
состояние системы в момент времени  Кроме того, необходимо отметить, что поведение одной из систем может быть проанализировано с помощью другой. Например, поведение маятника (системы
Кроме того, необходимо отметить, что поведение одной из систем может быть проанализировано с помощью другой. Например, поведение маятника (системы 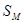 ) может быть изучено с помощью электрического колебательного контура (системы
) может быть изучено с помощью электрического колебательного контура (системы  , т.е. маятник или контур, взаимодействует с внешней средой
, т.е. маятник или контур, взаимодействует с внешней средой 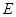 , то появляется входное воздействие
, то появляется входное воздействие 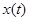 (Внешняя сила для маятника и источник энергии для контура) и непрерывно-детерминированная модель такой системы будет иметь вид
(Внешняя сила для маятника и источник энергии для контура) и непрерывно-детерминированная модель такой системы будет иметь вид
 является входным (управляющим) воздействием, а состояние системы
является входным (управляющим) воздействием, а состояние системы  .
. входных сигналов (входным алфавитом); конечным множеством
входных сигналов (входным алфавитом); конечным множеством 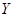 выходных сигналов (выходным алфавитом); конечным множеством
выходных сигналов (выходным алфавитом); конечным множеством 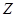 внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием
внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием  ; функцией переходов
; функцией переходов  ; функцией выходов
; функцией выходов  . Автомат, задаваемый F-схемой:
. Автомат, задаваемый F-схемой:  , - функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие
, - функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие  - му такту при
- му такту при  через
через  . При этом, по условию,
. При этом, по условию,  а
а 
 дискретного времени
дискретного времени  автомат находится в определенном состоянии
автомат находится в определенном состоянии  состояний автомата, причем в начальный момент времени
состояний автомата, причем в начальный момент времени  он всегда находится в начальном состоянии
он всегда находится в начальном состоянии  . В момент
. В момент 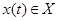 и выдать на выходном канале сигнал
и выдать на выходном канале сигнал  , переходя в состояние
, переходя в состояние  . Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита
. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита  на множество слов выходного алфавита
на множество слов выходного алфавита  , подавать в некоторой последовательности буквы входного алфавита
, подавать в некоторой последовательности буквы входного алфавита  , т.е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита
, т.е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита  …, образуя выходное слово.
…, образуя выходное слово. , подается некоторый сигнал
, подается некоторый сигнал  -м такте в новое состояние
-м такте в новое состояние  и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для
и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для  -автомата первого рода, называемого также автоматом Мили,
-автомата первого рода, называемого также автоматом Мили,


 и
и  , полностью задающие
, полностью задающие  и
и 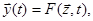 когда система
когда система  детерминированная и на её единственный вход поступает дискретный сигнал
детерминированная и на её единственный вход поступает дискретный сигнал  .
. , работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу
, работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу  определенный выходной сигнал
определенный выходной сигнал  , т.е. реализует логическую функцию вида
, т.е. реализует логическую функцию вида .
. и
и  происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F -автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может, как следует из
происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F -автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может, как следует из  , несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, - которое уже не может быть изменено данным входным сигналом.
, несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, - которое уже не может быть изменено данным входным сигналом.


