
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывно-стохастические модели ⇐ ПредыдущаяСтр 5 из 5
Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (англ. queueing system), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания. Основные соотношения В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т.д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т.е. стохастический характер процесса их функционирования. Остановимся на основных понятиях массового обслуживания, необходимых для использования Q- схем, как при аналитическом, так и при имитационном. В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью {
Потоком неоднородных событий называется последовательность
Прибор обслуживания заявок
Комбинированные модели
Наиболее известным общим подходом к формальному описанию процессов функционирования систем является подход, предложенный Н.П. Бусленко. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т.е. по сравнению с рассмотренными является обобщенным (универсальным) и базируется на понятии агрегативной системы (от англ. aggregate system), представляющей собой формальную схему общего вида, которую будем называть А-схемой Основные соотношения Анализ существующих средств моделирования систем и задач, решаемых с помощью метода моделирования на ЭВМ, неизбежно приводит к выводу, что комплексное решение проблем, возникающих в процессе создания и машинной реализации модели, возможно лишь в случае, если моделирующие системы имеют в своей основе единую формальную математическую схему, т.е. А -схему. Такая схема должна одновременно выполнять несколько функций: являться адекватным математическим описанием объекта моделирования, т.е. системы S, служить основой для построения алгоритмов и программ при машинной реализации модели М, позволять в упрощенном варианте (для частных случаев) проводить аналитические исследования. Приведенные требования в определенной степени противоречивы. Тем не менее в рамках обобщенного подхода на основе А- схем удается найти между ними некоторый компромисс. По традиции, установившейся в математике вообще и в прикладной математике в частности, при агрегативном подходе сначала дается формальное определение объекта моделирования - агрегативной системы, которая является математической схемой, отображающей системный характер изучаемых объектов. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Если некоторые из полученных подсистем оказываются в свою очередь еще достаточно сложными, то процесс их разбиения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи моделирования могут считаться удобными для математического описания. В результате такой декомпозиции сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней.
В качестве элемента А- схемывыступает агрегат, а связь между агрегатами (внутри системы S и с внешней средой Е) осуществляется с помощью оператора сопряжения R. Очевидно, что агрегат сам может рассматриваться как А- схема, т.е. может разбиваться на элементы (агрегаты) следующего уровня. Будем полагать, что переход агрегата из состояния В начальный момент времени
Обозначим полуинтервал времени
Совокупность случайных операторов V и U рассматривается как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний
В множестве состояний Z выделяется такое подмножество
Таким образом, под агрегатомбудем понимать любой объект, определяемый упорядоченной совокупностью рассмотренных множеств Т, X, Y, Z, Последовательность входных сигналов, расположенных в порядке их поступления в А- схему, будем называть входным сообщением или
Заключение
В ходе написания этой курсовой работы были выполнены поставленные задачи, а именно раскрыты основные понятия данного раздела науки, как математическое моделирование, при помощи математических схем. В данной курсовой рассмотрены самые распространенные схемы математического моделирования систем, при их детальном изучении нами был сделан вывод, что математические схемы удобны для проектирования, после которого можно более детально подойти к физическому построению требуемых моделей, а так же в ходе написания работы были рассмотрены на примерах некоторые из математических моделей. В заключении можно сказать, что этой аспект науки нужно интенсивно развивать, так как он, на данный момент времени, при построении больших (масштабных) работ, мало эффективен из - за того, что мало построено моделей, исходя из которых можно развивать практически все отрасли, но прогресс не стоит на месте и каждый день приобретаются более глубокие данные в этом аспекте науки.
Список использованной литературы
1. Арсеньев Б.П. Интеграция распределенных баз данных - СПБ.: Лань, 2000. . Арсеньев Б.П., Яковлев С.А. Интеграция распределенных баз данных. - СПб.: Лань, 2000. . Борн Г. Форматы данных. - Киев: торгово-издательское бюро BHV, 199S. . Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1988. . Веников В.А., Веников Г.В. Теория подобия и моделирования. - М.: Высшая школа, 1984. . Гнеденко Б.Д., Коваленко И.Н. Введение в теорию массового обслуживания. - М.: Наука, 1987. . Головин Ю.А., Яковлев С.А. Применение языков моделирования в обучении методам программной имитации сложных систем // Тез. докл. 6-й Междунар. конф. «Региональная информатика - 98»; Ч. 1. - СПб, 1998. . Громов Г.Р. Очерки информационной технологии. - М.: Инфоарт., 1992. . Дегтярев Ю.И. Исследование операций. - М.: Высшая школа, 1986. . Ермаков С.М., Мелос В.Б. Математический эксперимент с моделями сложных стохастических систем. - СПб.: Изд. ГУ, 1993. . Имитационное моделирование производственных систем/ Под ред. А.А. Вавилова. - М.: Машиностроение; Берлин: Техник, 1983. . Инструментальные средства персональных ЭВМ. В 10 кн. - М.: Высшая школа, 1993. . Калашников В.В., Рачев С.Т. Математические методы построения стохастических моделей обслуживания. - М.: Наука, 1988.
. Калиниченко Л.А., Рывкин В.М. Машины баз данных и знаний - М.: Наука, 1990. . Каляное Г.Н. CASE структурный системный анализ. - М.: Лори, 1996. . Кандрашина Е.Ю., Литвинцева Л.В. Поспелов Д.А. Представление знаний о времени и пространстве в интеллектуальных системах, - М.: Наука, 1989. . Киндлер Е. Языки моделирования. - М.: Энергия, 198S. . Клеймен Дж. Статистические методы в имитационном моделировании. - М.: Статистика, 1978. . Кривулин Н.К. Оптимизация сложных систем при имитационном моделировании // Вестник Ленингр. Ун-та. 1990. №8. . Кулаичев А.П. Компьютерный контроль процессов и анализ сигналов. - М.: Информатика и компьютеры, 1999. . Линник И.Ю. Улучшение скорости сходимости метода Монте-Карло в некоторых задачах теории массового обслуживания // Кибернетика. №5. 1978. . Математическая теория планирования эксперимента / Под ред. С.М. Ермакова. - М.: Наука, 1983. . Марк Д.А., Мак-Гоуен К. SADT. - Методология структурного анализа и проектирования - М.: Метатехнология, 1993. . Моисеев И.Н. Математические задачи системного анализа. М.: Наука, 1981. . Мухин О.И. Компьютерная инструментальная среда. - Пермь: ПГТУ, 1991. . Назаров С.В. Операционные системы специализированных вычислительных комплексов: теория построения и системного проектирования. М.: Машиностроение, 1989. . Николис Г., Пригожий И. Познание сложного. Введение - М.: Мир, 1990.
|
||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.202.72 (0.036 с.) |
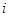 -го прибора обслуживания
-го прибора обслуживания 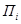 (рис. 1.1), состоящего из накопителя заявок
(рис. 1.1), состоящего из накопителя заявок 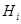 , в котором может одновременно находиться
, в котором может одновременно находиться 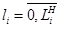 заявок, где
заявок, где 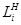 - емкость i -го накопителя, и канала обслуживания заявок (или просто канала)
- емкость i -го накопителя, и канала обслуживания заявок (или просто канала) 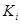 . На каждый элемент прибора обслуживания
. На каждый элемент прибора обслуживания 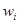 , на канал
, на канал 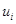 .
.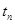 } = {
} = { 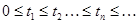 }, где
}, где 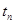 - момент наступления
- момент наступления 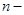 го события - неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности промежутков времени между
го события - неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности промежутков времени между 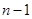 ) - м событиями {
) - м событиями { 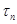 }, которая однозначно связана с последовательностью вызывающих моментов {
}, которая однозначно связана с последовательностью вызывающих моментов { 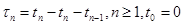 т.е.
т.е. 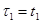
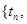
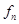 , где
, где 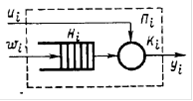
 в состояние
в состояние 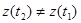 происходит за малый интервал времени, т.е. имеет место скачок
происходит за малый интервал времени, т.е. имеет место скачок 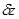 . Переходы агрегата из состояния
. Переходы агрегата из состояния 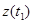 в
в 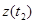 определяются собственными (внутренними) параметрами самого агрегата
определяются собственными (внутренними) параметрами самого агрегата 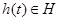 входными сигналами
входными сигналами 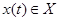 .
.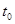 состояния z имеют значения, равные z°, т.е.
состояния z имеют значения, равные z°, т.е. 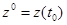 , задаваемые законом распределения процесса z(t) в момент времени
, задаваемые законом распределения процесса z(t) в момент времени 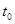 , а именно
, а именно 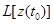 . Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала
. Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала 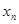 описывается случайным оператором V. Тогда в момент поступления в агрегат
описывается случайным оператором V. Тогда в момент поступления в агрегат 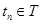 входного сигнала
входного сигнала 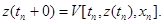
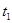 <
< 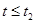 как
как 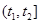 , а полуинтервал
, а полуинтервал 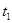 <
< 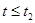 - как
- как 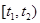 . Если интервал времени
. Если интервал времени 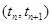 не содержит ни одного момента поступления сигналов, то для
не содержит ни одного момента поступления сигналов, то для 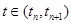 состояние агрегата определяется случайным оператором U в соответствии с соотношением
состояние агрегата определяется случайным оператором U в соответствии с соотношением
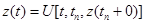 .
.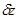 в моменты поступления входных сигналов х (оператор V) и изменений состояний между этими моментами
в моменты поступления входных сигналов х (оператор V) и изменений состояний между этими моментами 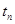 и
и 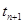 (оператор U). На оператор U не накладывается никаких ограничений, поэтому допустимы скачки состояний
(оператор U). На оператор U не накладывается никаких ограничений, поэтому допустимы скачки состояний  в моменты времени, не являющиеся моментами поступления входных сигналов х. В дальнейшем моменты скачков
в моменты времени, не являющиеся моментами поступления входных сигналов х. В дальнейшем моменты скачков 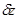 будем называть особыми моментами времени
будем называть особыми моментами времени 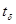 , а состояния
, а состояния 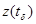 - особыми состояниями А- схемы. Для описания скачков состояний
- особыми состояниями А- схемы. Для описания скачков состояний 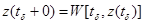 .
.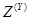 , что если
, что если 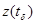 достигает
достигает 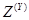 , то это состояние является моментомвыдачи выходного сигнала, определяемого оператором выходов
, то это состояние является моментомвыдачи выходного сигнала, определяемого оператором выходов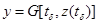 .
.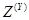 , Н и случайных операторов V, U, W, G.
, Н и случайных операторов V, U, W, G.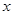 - сообщением. Последовательность выходных сигналов, упорядоченную относительно времени выдачи, назовем выходным сообщением или
- сообщением. Последовательность выходных сигналов, упорядоченную относительно времени выдачи, назовем выходным сообщением или 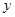 -сообщением.
-сообщением.


