Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие вычислительные приемы сложения и вычитания в пределах 100 и в какой последовательности изучают по различным программам математики начальных классов. Укажите теоретическую основу каждого приема.Содержание книги
Поиск на нашем сайте
Какие вычислительные приемы сложения и вычитания в пределах 100 и в какой последовательности изучают по различным программам математики начальных классов. Укажите теоретическую основу каждого приема. Вычислительные приемы сложения и вычитания в пределах 100 следующие: 1. Сложение и вычитание однозначных и двузначных чисел без перехода через разряд (25+3 и 25-3) 2.Сложение и вычитание однозначных и двузначных чисел с переходом через разряд (37+5 и 32-7) 3. Сложение и вычитание двух двузначных чисел без перехода через разряд (64-21и 64+21) 4. Сложение и вычитание двух двузначных чисел с переходом через разряд (28+54 и 62- 36) Приемы сложения и вычитания в пределах 100 начинают изучать с повторения теоретического материала. Теоретическим материалом всех этих случаев являются следующие темы:
1. Нумерация чисел в пределах 100; 2. Таблица сложения и соответствующие случаи вычитания в пределах 10 и 20; 3. Знание разрядного состава двузначных чисел; 4. Знание законов сложения (переместительного и сочетательного) и вывода из них: к единицам удобнее прибавлять (вычитать) единицы, а к десяткам десятки; 5. Действия сложения и вычитания как: сложение числа к сумме, вычитание числа из суммы, прибавление суммы к числу, вычитание суммы от числа, прибавление суммы к сумме и вычитанию суммы из суммы.
В учебниках математики разных программ предлагают различную последовательность изучения вычислительных приемов.
Рассмотрим подробнее последовательность в различных программах, анализируя учебники сначала по программе М.И. Моро: По программе М.И. Моро следующая последовательность изучения вычислительных приемов на сложение и вычитание:
Сложение и вычитание круглых десятков (двузначных разрядных чисел), которое сводится к сложению и вычитанию однозначных чисел, выраженных числом десятков.
Теоретическая основа данного приема следующая: 1. Знание разрядного состава чисел; 2. Соотношение между десятками и единицами; 3. Случаи сложения и вычитания в пределах 10.
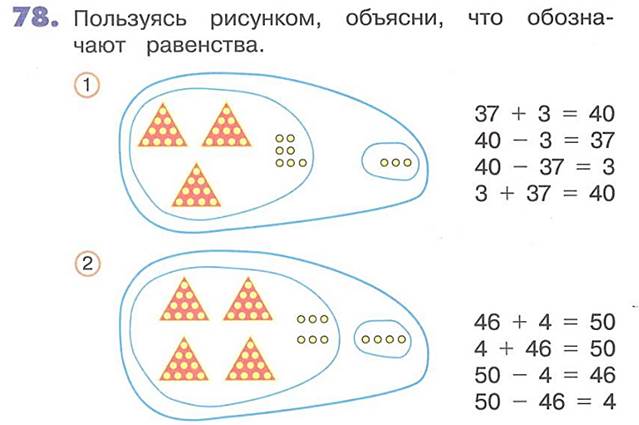
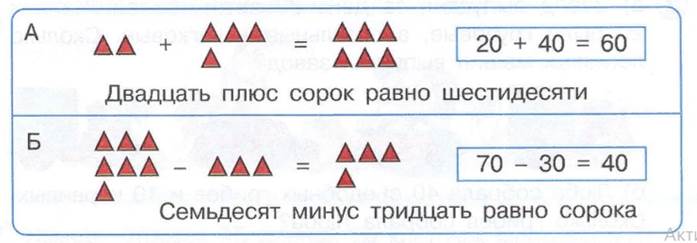
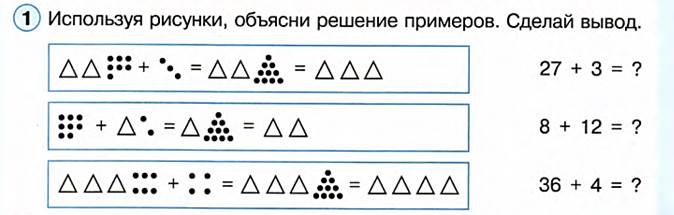
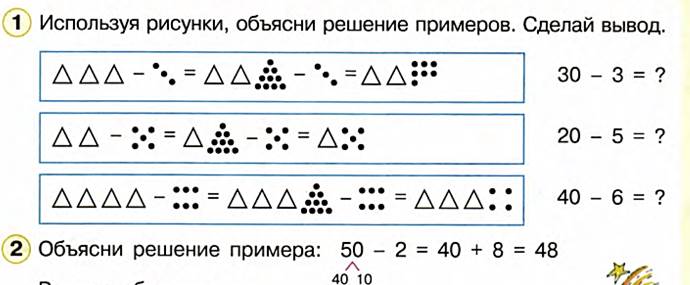
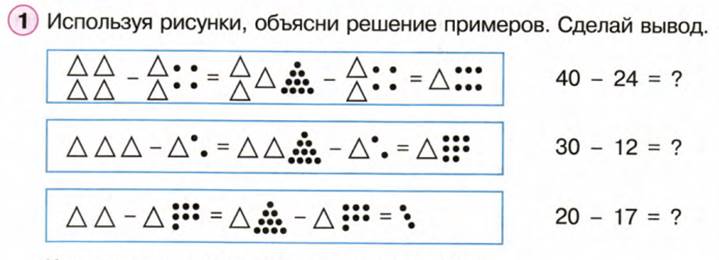
Например, чтобы к 20 прибавить 20, достаточно к 2 десяткам прибавить 4 десятка, будет 6 десятков, или 60, а, чтобы из 70 вычесть 50, достаточно из 7 десятков вычесть 5 десятка, будет 2 десятка, или 20. Объяснение решение двух-трех примеров иллюстрирующих рисунками и такой записью:
По программе Моро прием рассматривается во втором классе, первой части учебника:
М2М, часть 1, стр. 57 Является подготовительным этапом в изучении устных случаев сложения и вычитания.
2. Рассматривают свойства сложения числа к сумме, пользуясь которой и раньше усвоенными знаниями, вводят приемысложения двузначного числа и разрядного без перехода через разряд, случаи: 46+20, 46+2. Здесь же, используется прием перестановки слагаемых, рассматривают случаи 2+46.
По программе Моро рассмотрение данного приема выглядит следующим образом:
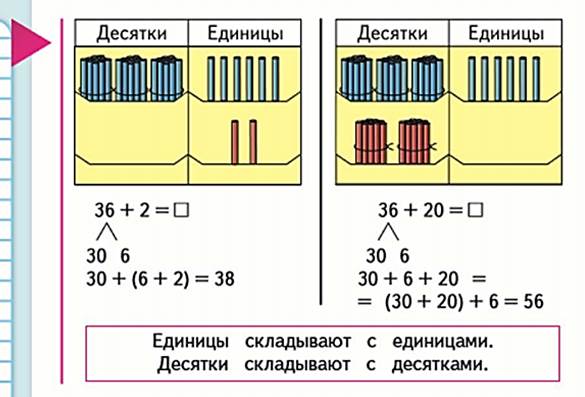
М2М, часть 1, стр. 58 В случае 46+2 предлагается применить сочетательное свойство сложения: 40+(6+2)=48 В случае 46+20 предлагается применить переместительное свойство вместе с сочетательным: 40+6+20=(40+20)+6=66 Вывод, по программе Моро, дают следующий: Единицы складывают с единицами. Десятки складывают с десятками. Этот вывод отражает принцип поразрядного сложения и вычитания чисел в пределах 100.
3. Вычитание числа из суммы и приемы вычитания из двузначного неразрядного числа разрядного без перехода через разряд, случаи: 48-30, 48-3 и 40-3. По программе Моро рассмотрение данного приема выглядит следующим образом:
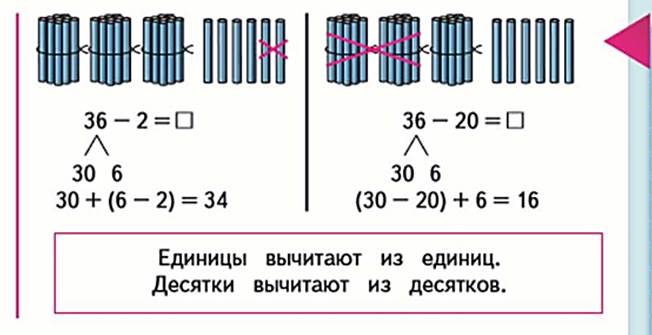
М2М, часть 1, стр. 59 Аналогично вычислительным приемам сложения: В случае 48-3 предлагается применить сочетательное свойство сложения: 40+(8-3)=45 В случае 48-30 предлагается применить переместительное свойство вместе с сочетательным: 48-30=(40-20)+6=26 Вывод, по программе Моро, дают следующий: Единицы вычитают из единиц. Десятки вычитают из десятков.
М2М, часть 1, стр. 60 В данном случае предлагается применить сочетательное свойство сложения:
96+4=90+(6+4)=100 М2М, часть 1, стр. 61 Ученики дают такое объяснение: 60-3. Заменю число 60 суммой удобных слагаемых 50 и 10; получили пример: от суммы чисел 50 и 10 отнять 3; удобнее отнять 3 от 10, от второго слагаемого, и найденный результат(7) прибавить к 50, к первому слагаемому, будет 57 М2М, часть 1, стр. 62 7. Потом рассматривают свойство прибавления суммы к числу, на основании которой раскрывают табличные случаи сложения с переходом через десяток.Сложение двузначных и однозначных чисел с переходом через десяток. Используют прием прибавления по частям. По программе Моро рассмотрение данного приема выглядит следующим образом:
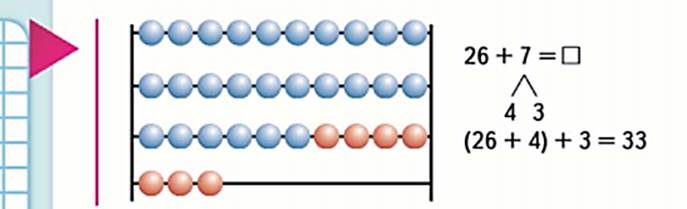
М2М, часть 1, стр. 66 26+7=33. Опираемся на прием сложения двух однозначных чисел с переходом через разряд. 26+(4+3)=33. В качестве дидактического материала Моро предлагает использовать счеты. Решая примеры, ученики дают соответствующие объяснения, например: 6+7. Заменю число 7 сумою удобных слагаемых 4 и 3; Получили например: к числу 6 прибавить сумму чисел 4 и 3; удобнее прибавить к 6 число 4, первое слагаемое 6 второе 4, и к полученному результату, 10, прибавить 3, сумма чисел равна 13. 47+9. Заменим число 9 суммой удобных слагаемых 3 и 6; получим пример: к 47 прибавить сумму чисел Из и 6; удобнее до 47 прибавить Из, первое слагаемое, и к найденному результату, до 50, прибавить 6, другое слагаемое, будет 56. Запись: 47+9=47 +6=56.
М2М, часть 1, стр. 67 В качестве дидактического материала Моро предлагает использовать счеты. М2М, часть 2, стр.4
65 + 14 = 60 + 5 + 10 + 4 = 60 + 10 + 5 + 4 = 79 Одновременно объясняют: заменим каждое число суммой разрядных слагаемых, пример: к сумме чисел 60 и 5 прибавить сумму чисел 10 и 4; удобнее прибавить первые слагаемые 60 и 10, потом вторые 5 и 4, прибавив результаты, получаем 79.
10. Прием вычитания из двузначного числа двузначного без перехода через разряд: По программе Моро рассмотрение данного приема выглядит следующим образом:
М2М, часть 2, стр.5
В качестве дидактического материала Моро предлагает использовать счетные палочки. Из 5 пучков убираем 2 пучка. Из 7 несвязанных палочек вычитаем 6, получаем 31.
М2М, часть 2, стр.29
По программе Моро также предлагается использовать дидактический материал при изучении темы – счетные палочки.
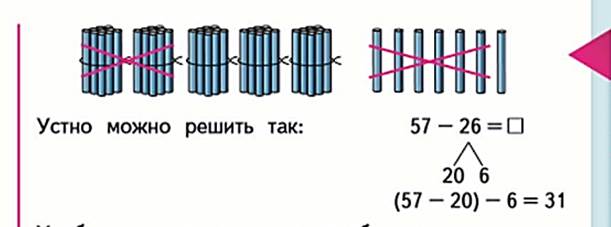
Сначала вычитают десятки, затем единицы. Из пяти пучков вычитаем 2 пучка. Из одного пучка и 2 палочек (12) вычитаем 4(сумма 2+2). Из 12 вычитаем 2, а затем 10 вычитаем еще 2. Получаем 2 пучка и 8 палочек. 28. 52-24=28 (52-20)-4=28 По программе Моро мы рассмотрели все случаи сложения и вычитания в пределах 100, отсутствует лишь 11 прием: Сложение двузначного числа с двузначным с переходом через десяток.
М2И, часть 1, стр.8
Дают сначала выражения исключительно с однозначными числами, а затем заменяют их на двузначные *10. Дают детям вспомнить разрядных состав чисел, подводя, задавая вопрос: «Можно ли в каждой паре найти значение второго выражения, пользуясь значением первого?».
2 и 3 прием (Приемысложения двузначного числа и разрядного без перехода через разряд, вычитание числа из суммы и приемывычитания из двузначного неразрядного числа разрядного без перехода через разряд) по программе Истоминой рассматривают, опираясь на упражнения, вместе: сложение и вычитание.
М2И, часть 1, стр.15 И 5, 6 приемы (Частные случаи прибавления к двузначным однозначных чисел, когда в сумме получается круглое число, вычитания однозначного числа из круглого, вычитания двузначного числа из круглого) также рассматриваются вместе: сложение и вычитание.
М2И, часть 1, стр.21 Истомина предлагает воспользоваться моделями десятков и единиц, если у учеников возникнут трудности.
М2И, часть 1, стр.54
Приемы Истомина выводит через интересные упражнения.
М2И, часть 1, стр.101
7.Сложение двузначных и однозначных чисел с переходом через десяток.
М2И, часть 1, стр.94 В качестве дидактического материала Истомина предлагает использовать треугольники с кармашками по 10 кружочков на каждом и отдельные куржочки. М2И, часть 1, стр.107
М2И, часть 1, стр.108 Вывод приема также через интересные, наглядные упражнения. 9 и 10 приемы (Случай сложения двузначного числа и двузначного без перехода через разряд, прием вычитания из двузначного числа двузначного без перехода через разряд) В учебниках по программе Истоминой подробно не рассматривается, переходят сразу к 11. А это значит, что их нужно будет выводить самостоятельно.
М2И, часть 2, стр. 12 М2И, часть 2, стр. 21 В понимании приема детям в помощь, по программе Истоминой, предлагаются рассуждения героев помощников учебника. По программе Л.Г. Петерсон приемы рассматриваются с первого класса, 3 части учебника. Последовательность значительно отличается от двух предыдущих программ. М1П, часть 3, стр.46 В учебниках сначала вспоминают разрядный состав числа, а затем переходят к самому приему:
М1П, часть 3, стр.49 В качестве наглядности используют треугольники (можно использовать в качестве наглядного пособия на доске) М1П, часть 3, стр.68 Сначала с данным приемом знакомятся в первом классе, выводят правила: 1.Чтобы сложить двузначные числа, можно к десяткам прибавить десятки, а к единицам – единицы. 2. Чтобы вычесть двузначные числа, можно из десятков вычесть десятки, а из единиц единицы. Затем во втором классе, 1 части этот прием повторят, с дополнением новых знаний.
М2П, часть 1, стр.10 4.Частный случай прибавления к двузначным однозначных чисел, когда в сумме получается круглое число:
М2П, часть 1, стр.12 Можно использовать наглядный материал: треугольники и кружки. 27 +3 = Два треугольника и 7 кружков + 3 кружка => 7 кружков + 3 кружка = 10 кружков или 1 треугольник + 2 треугольника = 3 треугольника или 30. 5. Вычитание однозначного числа из круглого:
М2П, часть 1, стр.16 Аналогично прошлому приему, работа с наглядным пособием. 6.Вычитания двузначного числа из круглого вида:
М2П, часть 1, стр.18 Аналогично прошлому приему, работа с наглядным пособием. 7 и 8:Сложение двузначного и однозначного и сложение двузначного числа с двузначным с переходом через десяток:
М2П, часть 1, стр.23 Решая примеры, ученики дают соответствующие объяснения, например: 8+5. Заменю число 5 сумою удобных слагаемых 2 и 3; Получили например: к числу 8 прибавить сумму чисел 2 и 3; удобнее прибавить к 8 число 2, первое слагаемое 8 второе 2, и к полученному результату, 10, прибавить 3, сумма чисел равна 13. 18+25. Заменим число 25 суммой удобных слагаемых 20 и 5; получим пример: к 18 прибавить удобнее всего 20, получим 18+20=38, оставшийся удобного слагаемое заменю также суммою удобных слагаемых 2 и 3; Получили например: к числу 38 прибавить сумму чисел 2 и 3; удобнее прибавить к 8 число 2, первое слагаемое 38 второе 2, получили 40 + 3=43 М2П, часть 1, стр.25 24-6 Ученик объясняет: "Заменю число 6 суммой удобных слагаемых 4 и 2; приведем пример: от 24 отнять сумму чисел 4 и 2; удобнее сначала отнять 4, первое слагаемое, а от найденного результата, от 20, отнять 2, второе слагаемое, получим 18".
43-24. Сначала вычитают десятки, затем единицы. Из 4 треугольников(десятков) вычитаем 2 треугольника. Из одного треугольника и 3 кружков (13) вычитаем 4(сумма 3+1). Из 13 вычитаем 3, а затем 10 вычитаем еще 1. Получаем 1 треугольник и 9 кружков = 19. Приемы 2 и 3 (По стандартной последовательности) (Сложения двузначного числа и разрядного без перехода через разряд, вычитание числа из суммы и приемы вычитания из двузначного неразрядного числа разрядного без перехода через разряд) по программе Петерсон подробно не рассматриваются. По программе И.И. Аргинской с вычислительными приемами знакомят во 2 классе, 1 части учебника. Многие приемы в данной программе не рассматриваются, а значит их нужно выводить самостоятельно. М2А, часть 1, стр.64 Аргинская предлагает в помощь наглядное пособие: счетные палочки. Выводы детям предстоит делать самостоятельно, опираясь на заданные вопросы учебника.
М2А, часть 1, стр.66 Далее детям предлагают вариант вычисления, где суммой заменяют оба двузначных числа. В помощь также могут пойти счетные палочки. Делается вывод: При сложении двузначных чисел удобно складывать десятки с десятками, а единицы – с единицами.
М2А, часть 1, стр.68 Единственная программа в которой выводят подробный алгоритм вычисления. М2А, часть 1, стр.72 К вычитанию также приводится подробный алгоритм вычисления. М2А, часть 1, стр.92 Также как и по программе Истоминой на помощь ученикам приходят герои-помощники учебника. Детям нужно сравнить случаи вычитания без перехода и с переходом через разряд. Следом идут вычисления: уменьшаемое и вычитаемое заменяем суммой разрядных слагаемых. Остальные приемы устных вычислений по программе подробно не рассматриваются, они появляются в упражнениях, перемешанные с другими. Вывод: практически все случаи (с одним минусом) рассматриваются по программам Моро и Истоминой. По программе Моро каждый случай разбирается подробно, у Истоминой случаи нужно вылавливать из упражнений, но интересных упражнений, помогающим детям в понимании приемов. По программе Петерсон отсутствуют 2 и 3 случай (по стандартной последовательности), последовательность приемов в данной программе сильно рознится с другими. По программе Аргинской рассматривают только 4 основных приема, что значит, на уроках нужно будет выводить остальные приемы самостоятельно.
Какие вычислительные приемы сложения и вычитания в пределах 100 и в какой последовательности изучают по различным программам математики начальных классов. Укажите теоретическую основу каждого приема. Вычислительные приемы сложения и вычитания в пределах 100 следующие: 1. Сложение и вычитание однозначных и двузначных чисел без перехода через разряд (25+3 и 25-3) 2.Сложение и вычитание однозначных и двузначных чисел с переходом через разряд (37+5 и 32-7) 3. Сложение и вычитание двух двузначных чисел без перехода через разряд (64-21и 64+21) 4. Сложение и вычитание двух двузначных чисел с переходом через разряд (28+54 и 62- 36) Приемы сложения и вычитания в пределах 100 начинают изучать с повторения теоретического материала. Теоретическим материалом всех этих случаев являются следующие темы:
1. Нумерация чисел в пределах 100; 2. Таблица сложения и соответствующие случаи вычитания в пределах 10 и 20; 3. Знание разрядного состава двузначных чисел; 4. Знание законов сложения (переместительного и сочетательного) и вывода из них: к единицам удобнее прибавлять (вычитать) единицы, а к десяткам десятки; 5. Действия сложения и вычитания как: сложение числа к сумме, вычитание числа из суммы, прибавление суммы к числу, вычитание суммы от числа, прибавление суммы к сумме и вычитанию суммы из суммы.
В учебниках математики разных программ предлагают различную последовательность изучения вычислительных приемов.
Рассмотрим подробнее последовательность в различных программах, анализируя учебники сначала по программе М.И. Моро: По программе М.И. Моро следующая последовательность изучения вычислительных приемов на сложение и вычитание:
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 2481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.217.86 (0.009 с.) |

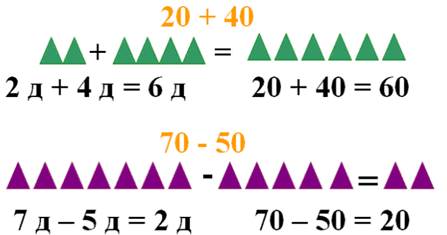

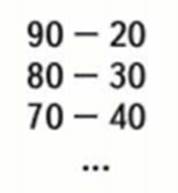 М2М, часть 1, стр. 57
М2М, часть 1, стр. 57 М2М, часть 1, стр. 57
М2М, часть 1, стр. 57